虽然不同企业中的被控对象千差万别，但大部分都是可以由微分方程来表示的，微分方程阶次的高低是由被控对象中储能部件的多少决定的。最简单的被控对象是仅有一个储能部件的单容对象（如单容水槽）。

1.单容水槽

单容水槽如图2-1所示。不断有水流入槽内，同时也有水不断由槽中流出。水的流入量Q i由调节阀开度μ加以控制，流出量Q o则由用户根据需要通过负载阀R来改变。被控变量为液位（水位）H，它反映水的流入量与流出量之间的平衡关系。下面分析水位在调节阀开度扰动下的动态特性。

在过程控制中，描述各种对象动态特性最常用的方式是阶跃响应，这意味着在扰动发生前，该对象原处于稳定平衡工况。

对于上述水槽，在起始稳定平衡工况下，有H＝H0，Q i0＝Q o0。在流出侧负载阀开度不变的情况下，当调节阀开度发生阶跃变化Δμ时，若水的流入量和流出量的变化量分别为ΔQ i＝Q i-Q i0，ΔQ o＝Q o-Q o0，则在任何时刻液位的变化ΔH＝H-H0均满足下述物料平衡方程为

式中：F为水槽横截面积。

当调节阀前后压差不变时，ΔQi与Δμ成正比关系，即

式中：kμ为取决于调节阀特性的系数，可以假定它是常数。

对于流出侧的负载阀，其流出量与水槽的液位高度有关，即

式中：k为与负载阀开度有关的系数，在开度固定不变的情况下，k可视为常数。

由于式（2-12）是非线性方程，给下一步的分析带来困难，因此应该在条件允许的情况下尽量避免。如果液位始终保持在其稳态值附近很小的范围内变化，那就可以将式（2-12）加以线性化，即

式（2-12）可以近似为

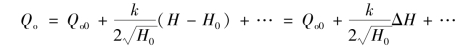
则

将式（2-11）和式（2-13）代入式（2-10）中得

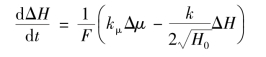
或

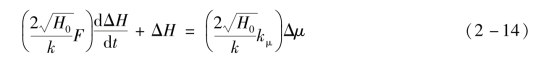
如果假设系统的稳定平衡工况在原点，即各变量都以各自的0值（H0＝0，μ0＝0）为平衡点，则可去掉式（2-14）中的增量符号，直接写成

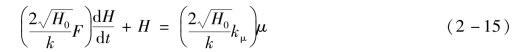
根据式（2-15）可得液位变化与调节阀开度变化之间的传递函数为

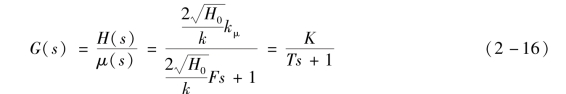
定义，则有：。

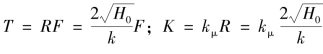式（2-16）是最常见的一阶惯性系统，它的阶跃响应曲线是指数曲线，如图2-3所示。

单容水槽液位变化与阻容充电回路的电容充电过程相同。实际上，如果把水槽的充水过程与RC回路的充电过程加以比较，就会发现两者虽不完全相似，但在物理概念上具有可类比之处。由图2-4可得RC充电回路的传递函数为

(www.daowen.com)

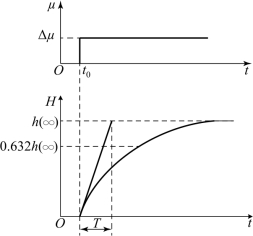
图2-3　单容水槽的阶跃响应曲线

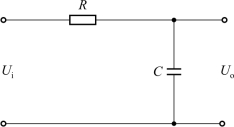
图2-4　RC充电回路

根据类比关系，由式（2-16）和（2-17）看出，对于水槽而言，水容（类比电容）C＝F，水阻（类比电阻）。

凡是只具有一个储蓄容积，同时有阻力的被控对象（简称单容对象）都具有相似的动态特性，单容水槽只是典型的代表。图2-5都属于这一类被控对象。

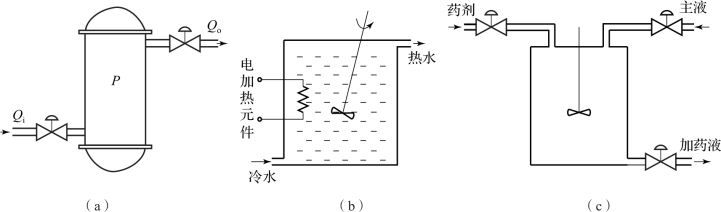
图2-5　其他单容对象

（a）储气罐；（b）电加热槽；（c）混合槽

2.具有纯迟延的单容水槽

对于如图2-1所示的单容水槽，如果进料调节阀流出的物料要经过一段较长距离管道传送才能到达水槽，即该调节阀开度μ变化所引起的流入量变化ΔQ i，需要经过一段传输时间T才能对水槽液位产生影响。

参照式（2-14），可得具有纯迟延的单容水槽的微分方程为

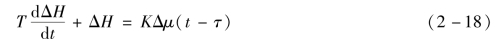
式中：τ为纯迟延时间；其余参数定义同上。

对应式（2-18）的传递函数为

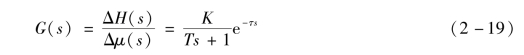
与式（2-16）相比，式（2-19）多了一纯迟延环节e-τs。

在生产过程的自动控制中，除某些特殊的纯迟延对象外，大多纯迟延是由于测量元器件、执行器安装位置引起的，在设计中应尽量减小这种纯迟延时间。

3.单容积分水槽

单容积分水槽如图2-6所示，与图2-1所示的单容水槽只有一个区别，即在它的流出侧装有一排水泵。

在图2-6中，水泵的排水量仍然可以用负载阀R来改变，但排水量并不随液位高低而变化。这样，当负载阀开度固定不变时，水槽的流出量也不变，因而在式（2-10）中有ΔQ o＝0。由此可以得到液位在调节阀开度扰动下的变化规律为

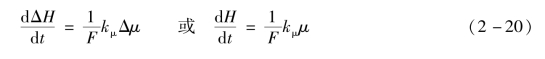
根据式（2-20）可得液位变化与调节阀开度变化之间的传递函数为

式（2-21）是一积分环节，积分时间T＝F／kμ，阶跃响应曲线为一条直线，如图2-7所示。

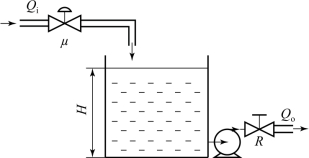
图2-6　单容积分水槽

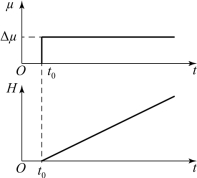
图2-7　单容积分水槽的阶跃响应曲线