路径点（结点）通常用工具坐标系｛T｝以相对于工作台坐标系｛S｝的位姿来表示。为了求得在关节空间形成所要求的轨迹，首先用逆向运动学将路径点转换成关节变量的值，然后对每个关节拟合一个光滑函数，使之从起始点开始，依次通过所有路径点，最后到达目标点。

对于每一段路径，各个关节运动时间均相同，这样可以保证所有关节同时到达路径点和终止点，从而得到工具坐标系应有的位置和姿态。

为了便于控制机器人，需要给定机器人在初始点和终止点的末端执行器的位姿。在规划机器人关节插值运动轨迹时，需要注意以下几点：

（1）抓取物体时，末端执行器的运动方向应该指向离开物体支承表面的方向，否则末端执行器可能与支承面相碰。

（2）若沿支承面的法线方向从初始点向外给定一个离开位置（提升点），并要求工具坐标系原点TCP经过此位置，这种离开运动是允许的。如果还给定由初始点运动到离开位置的时间，就可以控制提起物体运动的速度。

（3）对于手臂运动提升点的要求，同样也适用于终止位置运动的下放点（即必须先运动到支承表面外法线方向上的某点，然后再慢慢下移至终止点）。这样可获得正确的接近方向。

（4）对手臂的每一次运动，都设定四个点：初始点、提升点、下放点和终止点。

对于上述四个位置点，机器人运动满足的约束条件包括：

（1）初始点：①位置给定；②速度给定，通常为零；③加速度给定，通常为零。

（2）提升点：①位置给定；②位置与前一段轨迹末端位移相同；③速度与前一段轨迹末端速度相同；④加速度与前一段轨迹末端加速度相同。

（3）下放点：①位置给定；②位置与前一段轨迹末端位移相同；③速度与前一段轨迹末端速度相同；④加速度与前一段轨迹末端加速度相同；

（4）终止点：①位置给定；②速度给定，通常为零；③加速度给定，通常为零。

在关节空间中进行轨迹规划，需要由机器人在起始点、终止点处末端执行器的位姿利用机器人逆向运动学求解出相应的关节变量。对关节进行插值时，应满足一系列约束条件。在满足所要求的约束条件下，可以选取不同类型的关节插值函数生成轨迹，其中最常用的插值函数为多项式，如

θ（t）＝a0＋a1t＋a2t2＋…＋an－1tn－1＋ant n　（6-10）

在多项式插值中以三次多项式最为常用。如果机器人对路径的起始点、终止点以及一系列中间点的位移、速度和加速度等有更多要求时，三次多项式就无法满足需要，此时需要用更高阶的多项式对运动轨迹的路径段进行插值。高次多项式的主要缺点为求解多项式系数计算量大以及高次多项式对误差敏感，因此一般采用的多项式不超过五次，而且通常采用低次多项式组合的轨迹也同样能满足约束条件。

6.3.3.1　三次多项式插值

在机器人运动的过程中，由于相应于起始点的关节角度θ0已知，而终止点的关节角θf可以通过运动学反解获得。关节位移曲线θ（t）可以假定为一个多项式，如图6-12所示，并利用起始点关节和终止点的位移、速度和加速度约束，确定多项式各项系数。

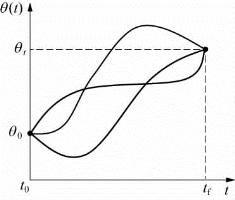
图6-12　两点之间的差值函数

为实现单个关节的平稳运动，轨迹函数θ（t）至少需要满足四个约束条件，即两端点位置约束和速度约束。

端点位置约束是指起始位姿和终止位姿分别所对应的关节角度。θ（t）在时刻t0＝0时的值是起始关节角度θ0，在终端时刻t f时的值是终止关节角度θtf，即

为满足关节运动速度的连续性要求，另外还有两个约束条件，即在起始点和终止点的关节速度要求，但在当前情况下可设定为零

由式（6-11）和式（6-12）给出的四个约束条件可以唯一地确定一个三次多项式，即

θ（t）＝a0＋a1t＋a2t2＋a3t3　（6-13）

由式（6-13）对时间求导，可以得到运动过程中的关节速度和加速度分别为

为求得三次多项式的系数a0、a1、a2和a3，将式（6-11）和式（6-12）所示的约束条件代入，可得

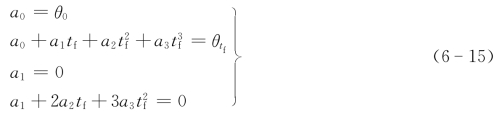
求解该方程组，可求得多项式系数为

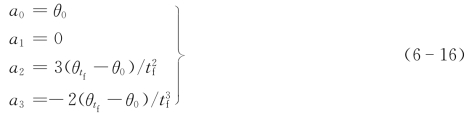
将上述系数代入式（6-13），可求得能满足连续平稳运动要求的三次多项式插值函数为

对式（6-17）求导，可得关节角速度和角加速度分别为

基于三次多项式的关节运动的位移曲线、速度曲线和加速度曲线如图6-13所示。

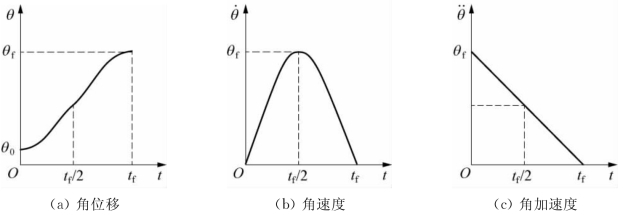
图6-13　三次多项式插值的关节运动轨迹

【例6-1】　设某一机器人的一个转动关节，其在执行一项作业时历时3 s。作业要求该关节运动平稳，且满足约束条件为：初始时，关节静止不动，θ0＝0°；运动结束时θf＝60°，此时关节速度为0。试确定能满足上述要求的多项式。

解：根据要求，可以对该关节采用三次多项式插值函数来规划其运动。已知θ0＝0°，θf＝60°，t f＝3 s，代入式（6-16）可得三次多项式的系数为：a0＝0.0，a1＝0.0，a2＝20.0，a 3＝－4.44。

由式（6-17）和式（6-18）可以确定该关节的位移、速度和加速度为

θ（t）＝20t2－4.44t3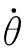，（t）＝40t－13.32t2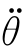，（t）＝40－26.64t

6.3.3.2　过路径点的三次多项式插值

多项式插值的方法也可应用于具有多个路径点（结点）的运动规划。如图6-14所示，机器人作业除在A、B点有位姿要求外，在路径点C、D也有位姿要求。对于这种情况，为保证运动平滑，将中间路径点（结点）在前一段运动终止点的位移、速度和加速度值作为后一段运动起始点的位移、速度和加速度，从而可以确定多项式的系数。

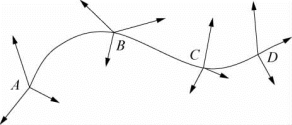
图6-14　机器人作业路径点

可以把所有路径点也看作“起始点”或“终止点”，通过逆向运动学求解得到相应的关节变量值，然后确定所要求的三次多项式插值函数。应用此方法可以把路径点平滑地连接起来。但是，在这些“起始点”和“终止点”的关节运动速度不再是零。

设路径点上的关节速度已知，在某段路径上，起始点为θ0和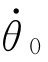，终止点为θtf和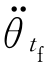，这时，确定三次多项式系数的方法与上述方法相同，只是速度约束条件变为

利用约束条件可以得到如下方程组

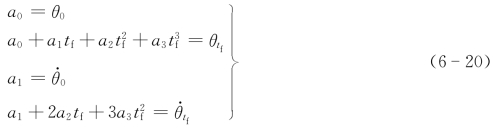
求解上述方程组，可得三次多项式的系数为

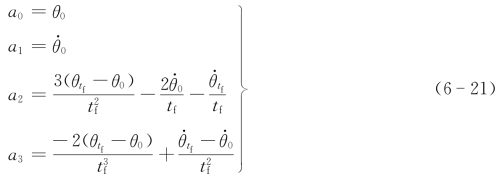
由上式确定的三次多项式描述了起始点和终止点具有任意给定位置和速度的运动轨迹，但接下来的问题就是如何确定路径点上的关节速度。具体方法为：基于工具坐标系的瞬时线速度和角速度（一般可以根据作业要求选定），利用机器人雅可比矩阵的逆矩阵确定机器人的关节速度。

6.3.3.3　用抛物线过渡的线性插值

在关节空间轨迹规划中，单纯线性插值会导致起始点和终止点的关节运动速度不连续，且加速度为无穷大，在两端点会造成刚性冲击。为消除刚性冲击，可以对如图6-15所示线性函数插值方法进行修正，即在线性插值两端点之间设置一段抛物线形的缓冲段，如图6-16所示。

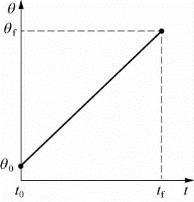
图6-15　两点间的线性插值轨迹

图6-16　带有抛物线过渡域的线性轨迹

为了确定过渡段的运动轨迹，假设两端的抛物线轨迹具有相同的持续时间t a，具有大小相同而符号相反的恒加速度。这种路径规划存在多个解，其轨迹不唯一，如图6-17所示。但是每条路径都对称于时间中点t h和位置中点θh。

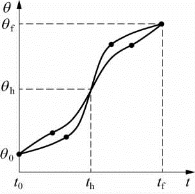
图6-17　轨迹的多解性与对称性

要保证路径轨迹的连续、光滑，即要求抛物线轨迹的终点速度必须等于线性段的速度，即满足以下关系

式中，θa为对应于抛物线持续时间t a的关节角度。θa的值可以按下式确定

设关节从起始点到终止点的总运动时间为t f，则t f＝2t h，由于

将式（6-23）和式（6-24）代入式（6-22）可得

(www.daowen.com)

当θ0、θf、t f已知时，可根据式（6-23）选择相应的和t a值，进而得到相应的关节运动轨迹。一般的方法是先选定加速度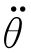的值，然后按式（6-25）求出相应的t a值，即

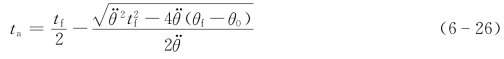
由式（6-26）可知，为保证t a有解，加速度值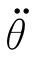须满足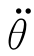2tf2－4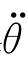（θf－θ0）≥0，即

当式（6-27）中的等号成立时，轨迹线性段的长度缩减为零，整个轨迹由两个过渡段组成，　这两　个过渡段在衔接处的斜率（关节速度）相等；加速度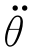的取值越大，则过渡段的长度越短，若加速度趋于无穷大，则轨迹还原至线性插值情况。

【例6-2】　θ0、θf和t f的含义同【例6-1】，若将已知条件变为θ0＝10°，θf＝70°，t f＝5 s，试设计一条带有抛物线过渡的线性轨迹。

解：根据题意，按式（6-27）定出加速度的取值范围，为此，将已知条件代入式（6-27）中，有≥9.6°／s2。

选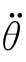1＝20°／s2，由式（6-27）算出过渡时间t a1，即

由式（6-23）可计算出过渡域终了时的关节位置θa1和关节速度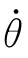1，可得

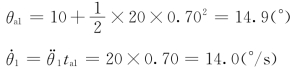
据上面计算得出的数值可以绘出如图6-18所示的轨迹曲线。

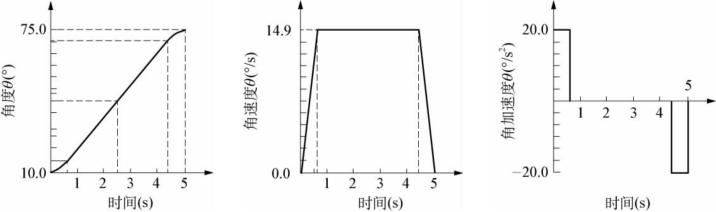
图6-18　带有抛物线过渡的线性插值

除了采用抛物线过渡的线性函数插值进行轨迹规划外，还可以采用等加速、等速和等减速运动规律、正弦运动规律等。

6.3.3.4　五次多项式轨迹

如果在某段路径的起始点和终止点都给定了关节的位置、速度和加速度，则可以用一个五次多项式进行插值，即

θ（t）＝a0＋a1t＋a2t2＋a3t3＋a4t4＋a5t5　（6-28）

上述多项式有6个系数a0，a1，…，a5，理论上必须有6个约束条件才能唯一地确定多项式的系数。根据起始点和终止点的位移、速度和加速度约束条件可得

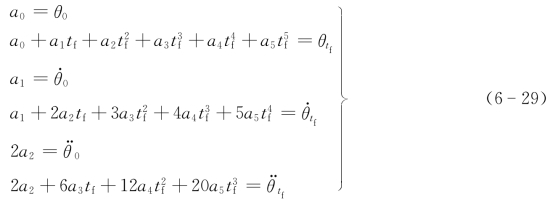
解上述方程组可以确定多项式系数a0，a1，…，a5。

6.3.3.5　“4-3-4”多项式轨迹

机器人每个关节的运动轨迹包含三段（图6-19）：第一段由初始点到提升点的轨迹用四次多项式表示；第二段（或中间段）由提升点到下放点的轨迹用三次多项式表示；最后一段由下放点到终止点的轨迹由四次多项式表示。

在每段轨迹中关节变量的多项式为

第一段

θ1（t）＝a14t4＋a13t 3＋a12t2＋a11t＋a10t∈［0，τ1f］　（6-30）

第二段

θ2（t）＝a23t3＋a22t2＋a21t＋a20t∈［0，τ2f－τ1f］　（6-31）

第三段

θ3（t）＝a34t4＋a33t3＋a32t2＋a31t＋a30t∈［0，τ3f－τ2f］　（6-32）

约束条件如下：

1）初始位置

（1）初始点位置θ1给定。

（2）初始点速度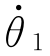给定，通常为零。

（3）初始点加速度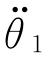给定，通常为零。

2）提升位置

（1）提升点位置θ2给定。

（2）提升点位置与前一段轨迹末端位移相同：θ2＝θ1（t＝τ1f）＝θ2（t＝0）。

（3）提升点速度与前一段轨迹末端速度相同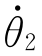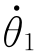：＝（t＝τ1f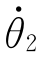）＝（t＝0）。

（4）提升点加速度与前一段轨迹末端加速度相同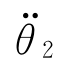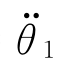：＝（t＝τ1f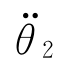）＝（t＝0）。

3）下放位置

（1）下放点位置θ3给定。

（2）下放点位置与前一段轨迹末端位移相同：θ3＝θ2（t＝τ2f）＝θ3（t＝0）。

（3）下放点速度与前一段轨迹末端速度相同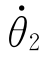：＝（t＝τ2f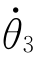）＝（t＝0）。

（4）下放点加速度与前一段轨迹末端加速度相同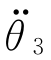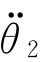：＝（t＝τ2f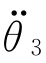）＝（t＝0）。

4）终止位置

（1）终止位置θ4给定。

（2）终止速度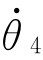给定，通常为零。

（3）终止加速度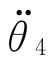给定，通常为零。

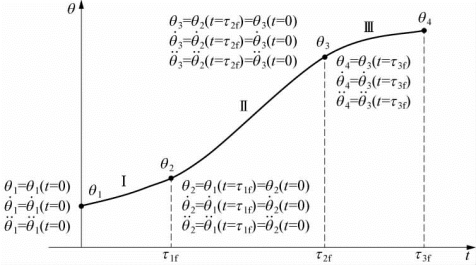
图6-19　“4-3- 4”多项式轨迹

第一段：

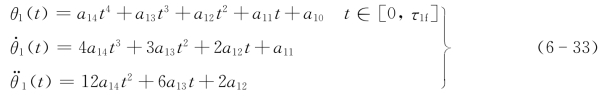
对于t＝0要满足此位置的约束条件为

第二段：

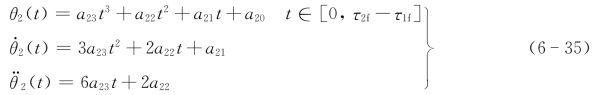
对于t＝0时第二段与第一段末了的位移、速度和加速度分别相同，故

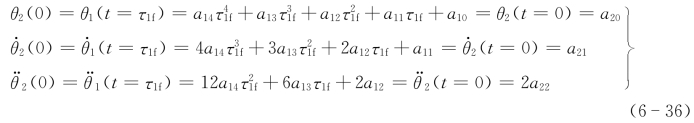
第三段：

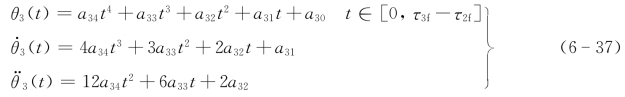
对于t＝0第三段与第二段末了的位移、速度和加速度分别相同，故

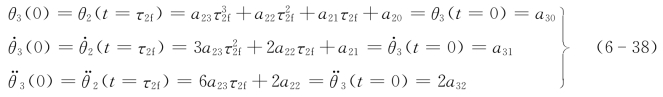
对于t＝τ3f第三段末了的位移、速度和加速度为

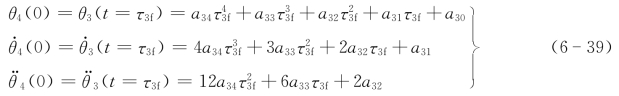
联立式（6-34）、式（6-36）、式（6-38）、式（6-39）可得

即

式中，矩阵M的结构便于计算未知系数，矩阵M的逆矩阵M－1存在（可利用MATLAB的矩阵求逆指令求得）。利用M－1可以求得各段多项式系数，结果可登录出版社网站（www．sstp．cn）“课件／配套资源”栏目参考。

6.3.3.6　“3-5-3”多项式轨迹

每个关节也由三段组成：第一段用三次多项式表示，第二段用五次多项式表示，最后一段用三次多项式表示。每一段多项式系数的计算方法可以参考“4-3-4”多项式轨迹的方法确定。