1)直线插补
空间直线插补是在已知该直线始末两点的位置和姿态的条件下,求各轨迹中间点(插补点)的位置和姿态。但是在大多数情况下,机器人沿直线运动时其姿态不变,所以无须进行姿态插补,即保持第一个示教点时的姿态。在有些情况下作业要求姿态变化,此时需要进行姿态插补。
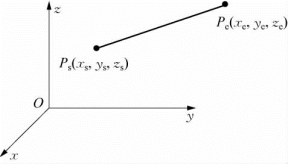
图6-7 空间直线插补
如图6-7所示,已知直线始末两点的坐标值P s(xs,ys,zs)、P e(x e,y e,z e)及姿态矩阵R s和R e,其中P s和P e是相对于基坐标系的位置。这些已知的位置和姿态通常是通过示教方式得到的。设v为要求的沿直线运动的速度,t s为插补时间间隔。
为减少实时计算量,示教完成后,可求出直线长度为
![]()
如果工具坐标系TCS在P 0和P e两点内做匀速运动,并设在t s间隔内的行程为d=vt s,则插补总步数N为L/d+1的整数部分,记为N=int(L/d)+1。
各轴增量分别为

各插补点坐标值递推表达式为

其中i=0,1,2,…,N。
2)基坐标平面上的圆弧插补
基坐标平面包括xOy平面、xOz平面以及yOz平面。以xOy平面上的圆弧为例,已知不在一条直线上的三点P 1、P 2、P3,如图6-8和图6-9所示,以及与这些点对应的工件坐标系TCS的姿态,并假定圆弧圆心位于基坐标系的原点。
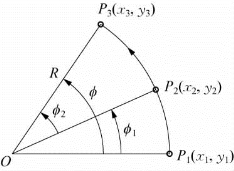
图6-8 由P1、P2、P3三点决定的圆弧
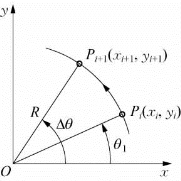
图6-9 圆弧插补
设v为沿圆弧运动速度;t s为插补时间间隔,则圆弧插补计算步骤为:
(1)由P 1、P 2、P 3三点确定圆弧半径R。
(2)确定总的圆心角φ=φ1+φ2,其中
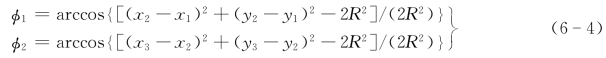
(3)计算t s时间内的角位移量Δθ=t sv/R。
(4)计算总插补步数(取整)N=int(φ/Δθ)+1。
据图6-9所示的几何关系求各插补点坐标。Pi+1点的坐标为(www.daowen.com)
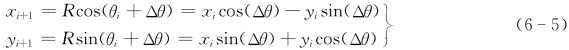
其中
xi=R cosθi,yi=R sinθi
由θi+1=θi+Δθ可以判断是否到达插补终点。若θi+1≤φ,则继续插补下去;当θi+1>φ时,则修正最后一步的步长Δθ,并以Δθ′=φ-θi表示,故平面圆弧位置插补表达式为
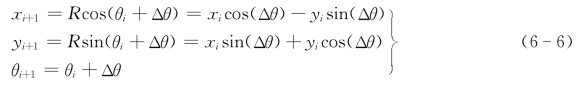
应该指出,当基平面上的圆弧的圆心不在基坐标系的原点时,可在其圆心处建立一个局部坐标系,从而可以利用上述插值方法计算出插值点的坐标,之后再利用坐标变换,将这些坐标值变换到基坐标系中。
3)空间圆弧插补
空间圆弧是指三维空间中不在基坐标平面上的圆弧,该圆弧插补问题可以转化成圆弧插补平面问题。空间圆弧插补可以按以下步骤进行:
(1)确定圆弧所在平面。如图6-10所示,设圆弧所在平面与基坐标系平面的交线分别为AB、BC、CA,则圆弧所在平面为ABC。由不在同一直线上的三点P 1、P2、P3可确定一个圆及三点间的圆弧,其圆心为OR,半径为R。
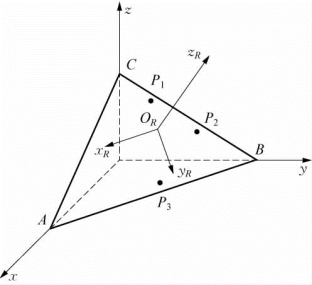
图6-10 基坐标系与空间圆弧平面坐标系的关系
建立圆弧平面上的插补坐标系,即以圆心OR为坐标系{x Ry RzR}的原点,z R为平面ABC的外法线方向;取过OR点且平行于直线AB的直线为x R轴,即x R∥AB;由y R=z R×x R可以确定y R轴,如图6-10所示。
(2)在空间平面上利用二维平面插补算法求出插补点坐标(ξi+1,ηi+1)。在平面ABC上依据基平面圆弧插补表达式(6-1)~式(6-6)完成圆弧插补,确定插补坐标为(ξi+1,ηi+1)。
(3)把空间平面圆弧上的插补点坐标(ξi+1,ηi+1)变换为在基坐标系中的三维坐标(xi+1,yi+1,zi+1)。为实现上述目标,需要建立坐标系{x Ry Rz R}与基坐标系{x y z}的坐标变换关系,即确定如图6-11所示的由圆弧所在平面坐标系{x Ry Rz R}到基坐标系{x 0y 0z0}的坐标变换矩阵。
设直线AB与x 0轴的夹角为α,因为x R∥AB,故x R轴与基坐标系x 0轴的夹角也为α,它与y 0轴的夹角为π/2-α;因为z0轴⊥AB,故x R轴与z 0轴的夹角为π/2。x R轴的单位向量n在基坐标系x 0轴、y 0轴、z 0轴的投影为n=[cosα -sinα 0]T。z R轴为平面ABC的外法向量,设zR轴与基坐标系z 0轴的夹角为θ。
如图6-11所示,过基坐标系原点O做直线OP⊥AB,OP交AB于N;把向量zR在平面ABC内平移,使得OR与点N重合,并取NM为单位长度,即NM=1;过M做MP⊥x 0O0y 0平面,垂足为P,可以证明P在直线ON上(因为AB⊥NM,AB⊥MP,故AB⊥平面NMP,因而,AB⊥NP;由于AB⊥ON,且O、N、P共面,故O、N、P共线)。过N做NQ∥x 0;过P做PQ∥y 0,两线交于Q点。
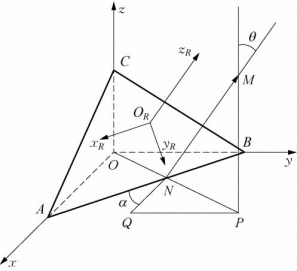
图6-11 空间圆弧平面坐标系与基坐标系的关系
因为AB与x 0轴夹角为α,故∠PNQ=π/2-α。NP=NM sinθ=sinθ,NQ=NP cos∠PNQ=sinθsinα,QP=NP sin∠PNQ=sinθcosα,MP=NM cosθ=cosθ,即zR轴的单位向量a在基坐标系的x 0轴、y 0轴、z0轴的投影分别为sinθsinα,sinθcosα,cosθ;即a=[sinθsinα sinθcosα cosθ]T。因为x R、y R、zR为右手正交坐标系,y R轴的单位向量o可以由zR的单位向量a和x R的单位向量n的叉积确定,即y R轴的单位向量o在基坐标系x 0轴、y 0轴、z0轴的投影为
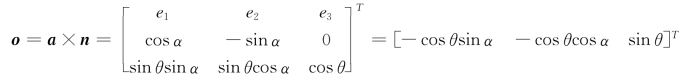
由式(2-11)可得坐标系{x Ry RzR}相对于基坐标系{x 0y 0z0}的位姿矩阵为
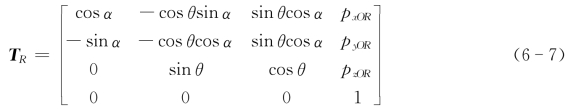
式中,pxOR、p yOR、pzOR为圆心OR在基坐标系下的坐标值。
因而,由式(2-17)可得坐标系{x Ry Rz R}中圆弧上的点C的坐标[ξi+1ηi+1]T与点C在坐标系{x 0y 0z0}中的坐标[xi+1yi+1zi+1]T之间的坐标变换为
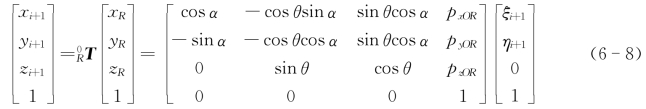
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








