5.7.3.1　拉格朗日动力学方程的建立

机器人在高速运动时，连杆的惯性力和惯性力矩对机器人末端执行器的运动轨迹精度和姿态精度有较大的影响，不能忽略不计，在这种情况下，需要研究机器人中作用力和运动的关系，这就是机器人的动力学问题。

通过机器人动力学方程研究机器人的动力学问题，特别是在已知驱动力的作用下，如何确定机器人各连杆的真实运动，是机器人动力学的根本问题。建立机器人动力学方程的方法有多种，如牛顿-欧拉迭代方法、凯恩方法、拉格朗日方程方法等，这些方法对于研究机器人的运动而言是等效的。在这些方法中，最直接的方法就是拉格朗日方程方法，它最大的优势在于：在不必求运动副之间作用力的情况下，就可以直接获得机器人的动力学方程。

对于一个n自由度机器人，其关节变量θ＝［θ1θ2…　θn］T，关节速度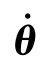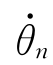＝［…　］T，可以由式（5-68）计算机器人连杆i的动能为K i，设连杆i的势能为Pi；则机器人的动能K和势能P分别为

机器人的拉格朗日函数L为

L（θ，）＝K－P　（5-71）

则关节i的驱动力（转动关节为驱动力矩，移动关节为驱动力Ni）为

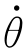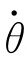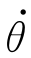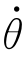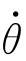应该指出，对于n自由度机器人，其动能K是关节变量θ1、θ2、…、θn和关节速度1、2、…、n共2n个变量的函数；而势能P仅仅是关节变量θ1、θ2、…、θn的函数；因此，拉格朗日函数L对关节速度i求偏导数∂L／∂θi，是把n个关节变量θ1、θ2、…、θn和其余n－1个关节速度1、2、…、i－1、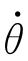i＋1、…、n当作“常量”，而只对关节速度i求导。

【例5-4】　试求如图5-19所示的平面2自由度机器人的机器人动力学方程。

解：1）求连杆质心坐标

图5-19　平面2自由度机器人

由图5-19可得连杆1和连杆2的质心坐标分别为

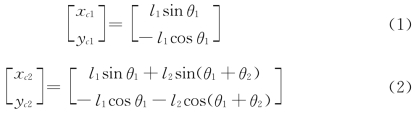
2）求连杆质心速度

由式（1）、式（2）可得

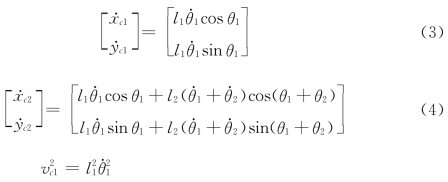
故

3）求系统动能

连杆1和连杆2的动能分别为

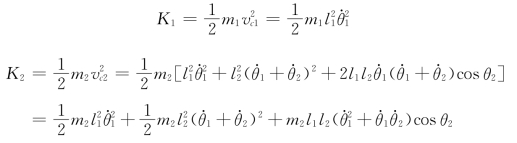
由式（5-69）可求得系统的总动能为

4）求系统势能

由式（5-70）可得系统的总势能为

P＝P 1＋P 2＝－m1l 1g cosθ1－m2g［l 1cosθ1＋l 2cos（θ1＋θ2）］　（6）

5）求拉格朗日函数

将式（5）和式（6）代入式（5-71）可求得机器人的拉格朗日函数为

6）求关节驱动力

将式（7）代入式（5-72）可以求得两个关节的驱动力矩为

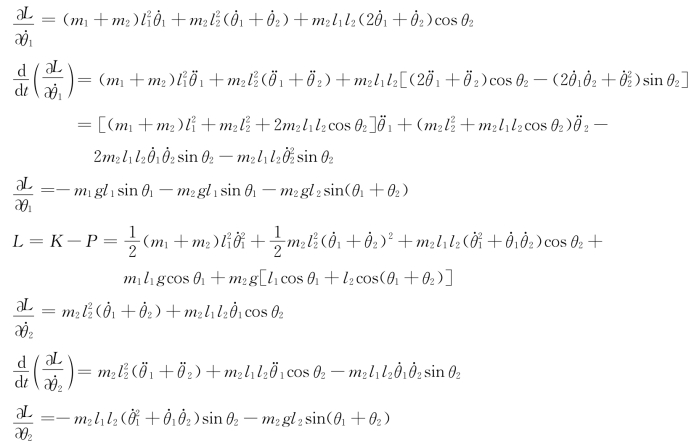
关节1和关节2的驱动力矩为

即

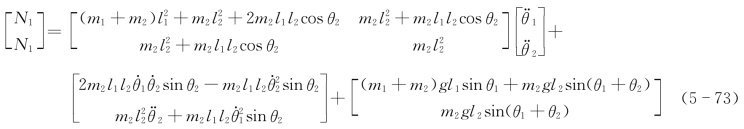(www.daowen.com)

或

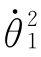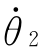式中，含和项为离心惯性力项；含项为科里奥利惯性力项；含mig项为重力项。一般的机器人动力学方程是时变、多变量、非线性、强耦合的特点。

5.7.3.2　拉格朗日动力学方程的结构

由式（5-68）可以求得机器人所有连杆的动能之和为

式中，n阶对称方阵M（θ）称为机器人的质量矩阵，因为机器人的动能总为正值，故M（θ）是正定矩阵；矩阵中的每个元素是n个关节变量θ1、θ2、…、θn的函数。矩阵对于n自由度机器人，由式（5-72）求出的关节驱动力方程有n个，由它们组成的方程组为

N＝M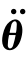（θ）＋H（θ，）＋G（θ）　（5-76）

式中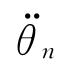，＝［…　］T；N＝［N 1N 2…　Nn］T为关节驱动力向量；n×1矩阵H（θ，）为惯性力项（包括离心惯性力和科里奥利惯性力），它是机器人关节变量、关节速度以及机器人位置和速度的函数；位置n×1矩阵G（θ）为重力向量，它是机器人位置的函数。式（5-73）为平面2自由度机器人的形如式（5-76）的动力学方程。

也可以将式（5-76）中的离心力项和科里奥利力项分开，式（5-76）可改写为

N＝M（θ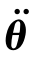）＋C（θ）［θ2］＋V（θ）［θθ］＋G（θ）　（5-77）

式中，［θ2］＝［…　］T为n×1阶向量；关节速度积向量［θθ］＝［θ1θ2θ1θ3…　θn－1θn］T为n（n－1）／2×1阶向量；n×n矩阵C（θ）为离心力系数矩阵，它仅仅是机器人位置的函数；n×n（n－1）／2矩阵V（θ）为科里奥利惯性力系数矩阵；n×1矩阵G（θ）为重力向量。式（5-74）为平面2自由度机器人的形如式（5-77）的动力学方程。

说明：式（5-76）和式（5-77）中，连杆i的驱动力N i＝d（∂L／∂）／d t－∂L／∂θi一般是耦合方程，这里的耦合是指某一关节的驱动力或力矩中包含有其他关节变量或关节变量导数。由于机器人动力学方程一般包含离心力项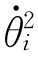和科里奥利力项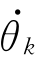，求解较为困难。

式（5-76）或式（5-77）左边仅为实现等式右边机器人连杆的运动时，机器人的关节所需要提供的驱动力N＝［N 1N 2…　Nn］T；它没有涉及连杆运动副受到的摩擦力τf（θ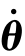，）＝［τf1τf2…　τfn］T以及连杆受到的其他阻力等效到关节上的当量阻力τR（θ）＝［τR1τR2…　τRn］T；如果考虑到这些力的作用，式（5-76）应改写为

5.7.3.3　拉格朗日动力学方程的应用

拉格朗日动力学方程可以解决以下两类问题：

（1）正问题。已知关节变量θ＝［θ1θ2…　θn］T、关节速度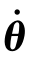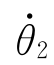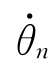＝［…　］T和关节加速度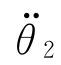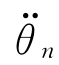＝［…　］T，求每个关节的驱动力N＝［N 1N 2…　Nn］T。

（2）反问题。已知关节的驱动力N＝［N 1N 2…　Nn］T，求机器人的运动规律，即每个关节的变量θ＝［θ1θ2…　θn］T的运动规律。

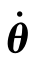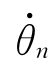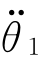
正问题求解较为简单，只需把关节变量θ＝［θ1θ2…　θn］T、关节速度＝［…　］T和关节加速度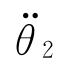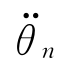＝［…　］T代入式（5-76）或式（5-77），经过矩阵运算即可求出驱动力N＝［N 1N 2…　Nn］T。

反问题，如机器人弧焊中的轨迹跟踪问题就属于此类。此时N＝［N 1N 2…　Nn］T为已知量，需要利用式（5-76）或式（5-77）的方程组求解关节变量θ＝［θ1θ2…　θn］T是否与规划的轨迹相符。由于该方程组为耦合的非线性方程组，求解析解较为困难，但一般可以利用数值计算的方法求得数值解。研究机器人的动力学问题可以借助机械系统动力学自动分析（automatic dynamic analysis of mechanical systems，ADAMS）软件进行。

参考文献

［1］Craig J J．Introduction to robotics mechanics and control［M］．3rd ed．［S．l．］：Person Education，Inc．Published as Prentice Hall，2005．

［2］Niku S B．Introduction to robotics：analysis，control，applications［M］．2nd ed．［S．l．］：John Wiley ＆ Sons，Inc．，2010．

［3］哈尔滨工业大学理论力学教研室．理论力学（Ⅱ）［M］．8版．北京：高等教育出版社，2016．

思考与练习

1.试求图3-17所示的平面3自由度机器人的速度雅可比矩阵和力雅可比矩阵，并求使机器人末端产生0F＝50i＋20j＋10k（i、j、k为基坐标系x轴、y轴、z轴的单位向量）的关节力。

2.试求图3-18所示的SCARA机器人的速度雅可比矩阵。

3.试画出一个3自由度机器人的机构运动简图，它的线速度雅可比矩阵为三阶单位阵。

4.某一3自由度机器人的运动学方程为

试求其速度雅可比矩阵0J。

图5-20　具有测力传感器的末端执行器

5.如图5-20所示为一具有测力装置的末端执行器示意图，已知传感器相对于腕部坐标系｛W｝的位姿为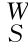T，工具坐标系｛T｝相对于腕部坐标系｛W｝的位姿为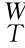T。力传感器的输出（相对于传感器坐标系｛S｝）为SF＝［Sf　Sτ］T（Sf∈R3为作用力，Sτ∈R3为作用力矩）；设末端执行器受到的作用力（相对于工具坐标系｛T｝）TF＝［Tf　Tτ］T（Tf∈R3为作用力，Tτ∈R3为作用力矩）。试求出从传感器输出力SF到末端执行器作用力TF的变换矩阵。

6.设矩阵R为旋转矩阵，试证明：

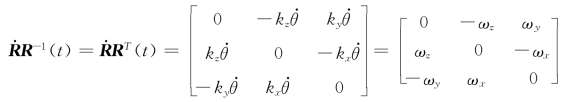
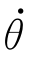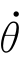其中［kxkykz］为瞬时旋转轴，［ωxωyωz］＝［kxkykz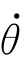］为瞬时旋转角速度向量。

7.试证明：对于姿态矩阵R和向量a以及a的反对称矩阵（a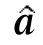）＝的关系：（Ra）＝RR T。