5.7.2.1 刚体惯性张量
为了便于描述刚体转动动能,引入描述刚体惯性的参量“惯性张量”。
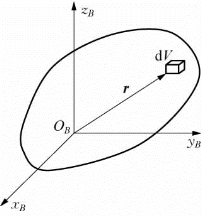
图5-17 描述刚体质量分布的惯性张量
如图5-17所示,在刚体上建立坐标系{B},设刚体在点Q处的位置向量![]() =r=[x y z]T,密度为ρ(r)。与向量r对应的反对称矩阵
=r=[x y z]T,密度为ρ(r)。与向量r对应的反对称矩阵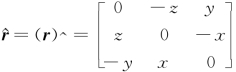 ,则坐标系{B}中的惯性张量可定义为
,则坐标系{B}中的惯性张量可定义为
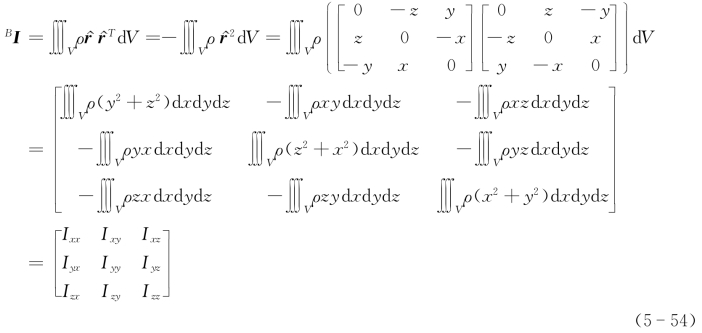
其中
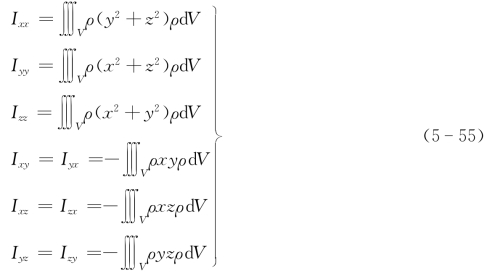
式中,Ixx为对x轴惯性矩;Iyy为对y轴惯性矩;Izz为对z轴惯性矩;Ixy=Iyx、Ixz=Izx、Iyz=Izy为惯性积。
5.7.2.2 以质心为基点的连杆(刚体)动能计算方法
刚体的惯性张量可以用于计算刚体的转动动能。如图5-18所示,为描述机器人连杆i相对于基坐标系{0}的运动,可以将动坐标系{i}建立在刚体质心Ci处。
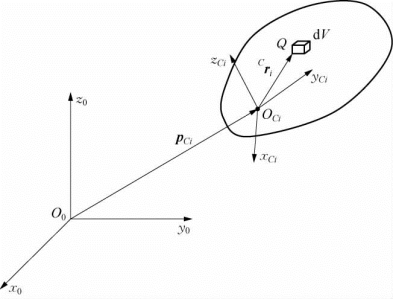
图5-18 动坐标系位于连杆i质心时刚体的动能
如图5-18所示,在刚体上Q点附件的一个微元体d V,质量为ρ(Cri)d V,则连杆i的质量为![]() ,为常量。
,为常量。
坐标系{B}中刚体的质心位置为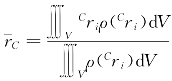 ,当坐标系{C}原点OC位于刚体质心C时,
,当坐标系{C}原点OC位于刚体质心C时,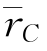 =0。
=0。
设连杆i的质心坐标系c i相对于坐标系{0}的位姿为0g Ci=![]() 。由式(2-16)可知连杆i上任一点Q在基坐标系{0}中的位置为0r=0p Ci+
。由式(2-16)可知连杆i上任一点Q在基坐标系{0}中的位置为0r=0p Ci+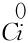 RCri;Q点相对于坐标系{A}的速度为
RCri;Q点相对于坐标系{A}的速度为
![]()
在连杆i上Q点附近的一个微元体d V,其质量为ρd V,该微元体的动能为
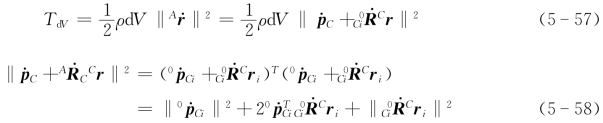
将式(5-58)代入式(5-57),可得整个刚体的动能K为

因坐标系原点位于刚体的质心![]() d V=0。刚体动能包括随质心Ci的平动动能T Di和绕质心轴的转动动能T Ri,它们分别为
d V=0。刚体动能包括随质心Ci的平动动能T Di和绕质心轴的转动动能T Ri,它们分别为
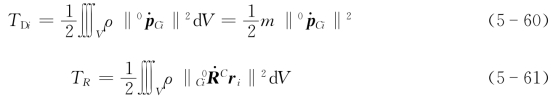
式(5-61)可以化简。由式(5-18)可知连杆i转动的角速度向量0ωi满足
![]() (https://www.daowen.com)
(https://www.daowen.com)
刚体转动角速度ω在坐标系{0}和坐标系{i}之间的关系为
![]()
现在面临的关键问题是,如何确定在坐标系{0}中描述的角速度张量0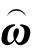 i,与坐标系{i}中描述的角速度张量C
i,与坐标系{i}中描述的角速度张量C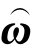 i之间的关系。
i之间的关系。
对于姿态矩阵R和向量a以及a的反对称矩阵(a)=a,存在以下关系式(参见本章末思考与练习第7题):![]() ,即
,即
(Ra) =R
=R R T (5-64)
R T (5-64)
因而,
![]()
由式(5-62)和式(5-64)可得![]() ,故
,故

将式(5-66)代入式(5-61)可得
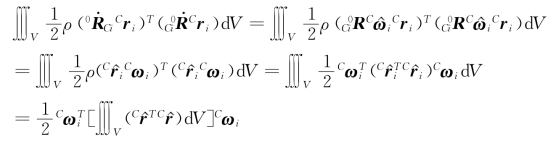
上式中利用了![]() 。又
。又
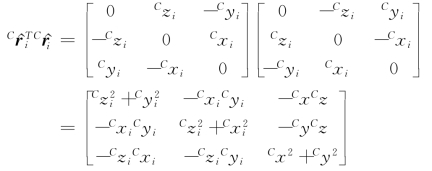
因而
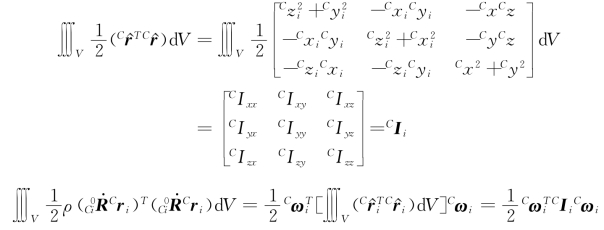
因为![]() ,故
,故
![]()
由式(5-59)和式(5-67)可得刚体动能为
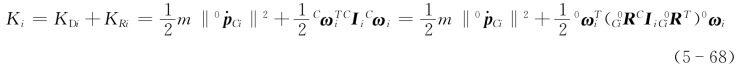
由式(5-68)可以看出,连杆动能包括随质心的平动动能和绕质心旋转的转动动能;连杆动能是连杆位姿的函数,也是质心速度以及连杆转动角速度的函数。在应用式(5-68)时,具体计算步骤如下:
(1)将机器人在某一时刻t的关节变量θ=[θ1θ2… θn]代入式(3-4)可求出连杆i上的D-H坐标系{i}相对于机器人基坐标系{0}的位姿矩阵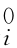 T=
T=![]()
(2)利用0T i=![]() 求出坐标{i}原点线速度
求出坐标{i}原点线速度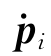 ;再利用式(5-19)求出连杆的转动角度0ωi。
;再利用式(5-19)求出连杆的转动角度0ωi。
(3)利用质心坐标系{Ci}与坐标系{i}的位置矩阵iT Ci求出质心坐标系{C}相对于基坐标系的位姿![]()
(4)利用上式可求出连杆i质心的速度0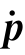 Ci。
Ci。
(5)将连杆i质心速度0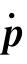 Ci、连杆转动角速度0ωi、质心坐标系{Ci}相对于机器人基坐标系{0}的姿态矩阵0R Ci、连杆i相对于其质心的惯性张量CI i代入式(5-68)可计算出连杆i的动能K i。
Ci、连杆转动角速度0ωi、质心坐标系{Ci}相对于机器人基坐标系{0}的姿态矩阵0R Ci、连杆i相对于其质心的惯性张量CI i代入式(5-68)可计算出连杆i的动能K i。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







