对于一个n自由度机器人，若已知机器人末端连杆受到的阻力f n（三维向量）和阻力矩M n（三维向量），它们可以合写成六维向量：。为了平衡机器人末端执行器受到的阻力f n和阻力矩M n，机器人关节1、关节2、…、关节n各需要提供的驱动力N＝［N 1N 2…　Nn］T为多大？

设机器人各连杆的关节变量为θ＝［θ1θ2…　θn］T，关节速度为＝；末端连杆的速度为。则在不计摩擦的前提下，根据能量守恒原律，单位时间内所有驱动力所做的功和阻力所做的功应该相等，即

，即

F nTV n＝N T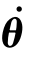　（5-50）

由式（5-31）可知V n＝J V，代入上式可得：F nTJ V＝N T，故F nTJ V＝N T，两边取矩阵转置可得

N＝JF n＝J FF n　（5-51）

式（5-51）中的J F称为机器人力雅可比矩阵，它是机器人速度雅可比矩阵J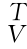的转置。

与速度雅可比矩阵的作用相似，与机器人速度雅可比矩阵相关问题有两类：正向问题和逆向问题。

（1）正向问题。已知机器人末端连杆n受到的外力和力矩F n＝［fnxfnyfnzMnxMnyMnz］ T的情况下，求机器人各关节的驱动力N＝［N 1N 2…　Nn］T。(www.daowen.com)

（2）逆向问题。已知机器人各关节的输出力N＝［N 1N 2…　Nn］T，求在机器人末端连杆承受多大的外力和力矩F n＝［fnxfnyfnzMnxMnyMnz］T。

第一类问题（正向问题）求解方法：只要确定当前时刻机器人的力雅可比矩阵J F，并把J F和外力F n代入式（5-51）即可解决。

第二类问题（逆向问题）求解方法：由式（5-51）中的雅可比矩阵J F和N＝［N 1N 2…　Nn］T为已知量，要确定F n＝［fnxfnyfnzMnxMnyMnz］T就变成了如下代数方程组求解的问题

上述方程组是否有解与力雅可比矩阵J F的“秩”有关。线性代数中线性方程组有解的充分必要条件是：系数矩阵J F的“秩”Rank（J F）和增广矩阵［J FN］的秩相等，即Rank（J F）＝Rank（［J FN］），否则线性代数方程组（5-52）无解。

若式（5-52）出现“无解”情况，意味着在机器人末端连杆（末端执行器）工作空间的某个位置，指定的关节力在机器人末端产生的输出力的某些分量之间出现矛盾，此时机器人处于“奇异位姿”。

一般的代数方程组有规范的求解方法，即通过对增广矩阵进行初等行变换，获得“阶梯矩阵”（最简行矩阵），就可以判断方程组是否有解以及解的结构。

上述方法适用于静力平衡计算，在计算过程中没有考虑构件的重力、构件的惯性力和惯性力矩以及运动副摩擦力和摩擦力矩，一般可以用于机器人运动速度较低的场合。当机器人的连杆高速运动时，构件的惯性力和惯性力矩不能忽略，此时需要研究机器人动力学问题。