机器人若受到外部负载的作用，为保持受力平衡，需要确定每个关节输出的驱动力（包括力和力矩），这需要研究关节驱动力沿运动链的传递关系。以如图5-14所示的连杆i为研究对象，规定：

（1）为连杆i－1对连杆i施加的作用力；其反作用力为。

（2）为连杆i－1对连杆i施加的力矩；其反作用力矩为。

图5-14　连杆的静力平衡关系

连杆i受力平衡的条件是合外力和合外力矩（对坐标系｛i｝原点取矩）分别为0，则

当不计连杆重力时，式（5-46）变为

式（5-47）为相邻连杆i和连杆i＋1之间静力传递的递推式。

应用式（5-47）时，一般应在工具坐标系｛T｝中根据末端连杆受到的工作阻力F R和阻力矩M R求出末端连杆n对工作对象的作用力f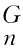和作用力矩τ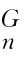；然后可以依据坐标系之间的姿态矩阵，按照式（5-47）依次求出所有相邻连杆之间的作用力。

对于转动关节，为了平衡连杆i上的力和力矩，需要在关节i上施加的力矩iτ（向量）为

对于移动关节，关节i上的驱动力为

说明：式（5-47）是计算机器人各相邻连杆之间作用力和力矩的递推关系式，但计算次序应该从机器人末端连杆（末端执行器）开始，先利用末端执行器受到的工作阻力，求出末端连杆n的关节驱动力，再利用式（5-47）依次计算出连杆n与连杆n－1、连杆n－1与连杆n－2、…、连杆2与连杆1之间的作用力和力矩。

【例5-3】　试求如图5-15所示的平面2自由度机器人的力和力矩传递关系。

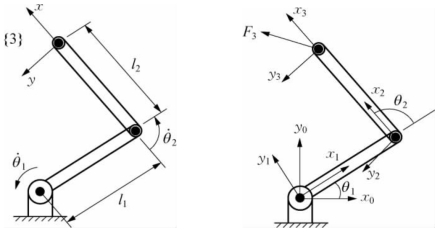
图5-15　平面2自由度机器人

解：设末端执行器受到的工作阻力在坐标系｛3｝中为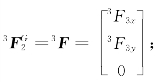设该力在基坐标系｛0｝中的坐标为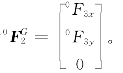

由【例5-2】可知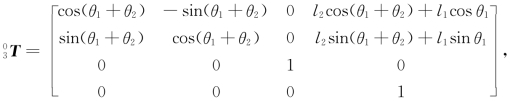：则坐标系｛3｝相对于坐标系｛0｝的姿态矩阵为

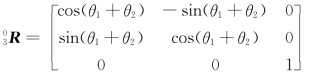(www.daowen.com)

根据式（2-12）所示的向量在两个坐标系之间的转换关系可得

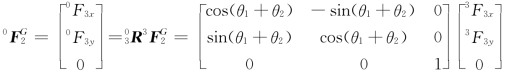
即工作阻力在坐标系｛3｝中的坐标与其在基坐标系｛0｝中的坐标关系为

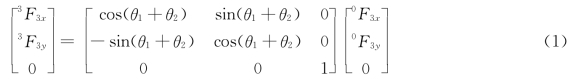
连杆2（末端执行器）对外工作对象输出的作用力在坐标系｛3｝中为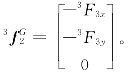

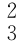由【例5-2】可知即坐标系｛3｝相对于坐标系｛2｝的姿态矩阵R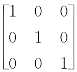＝，故根据式（2-12）所示的向量在两个坐标系之间的转换关系，可求得连杆2（末端执行器）对外工作对象输出的作用力和作用力矩在坐标系｛2｝中分别为

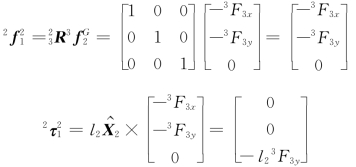
由【例5-2】可知即坐标系｛2｝相对于坐标系｛1｝的姿态矩阵故由式（5-47）可得连杆1对连杆2的作用力在坐标系｛1｝中分别为

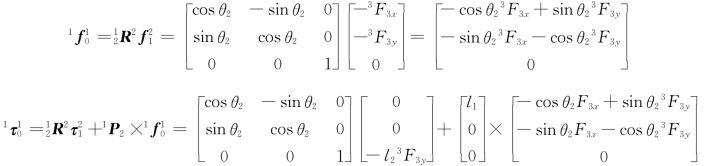
由式（5-48）可以求出两个关节的驱动力矩分别为

故

即

把式（1）代入式（2）可得

即该机器人在基坐标系｛0｝中的雅可比矩阵为J F为

对比【例5-1】结果可知力雅可比矩阵与速度雅可比矩阵之间的关系为J F＝J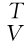，即力雅可比矩阵为速度雅可比矩阵的转置。