对于n自由度串联机器人,其第i个连杆的运动,是前第1、第2、…、第i-1个连杆相对于其自身轴线Z1、Z2、…、Zi-1的运动,通过运动链中依次传递到连杆i上后,与连杆i相对于其自身轴Zi的运动“相叠加”后的合成运动结果。因为是串联机器人,连杆i+1、连杆i+2、…、连杆n的运动对连杆i的运动无影响。
1)角速度传递
为了研究上述运动的传递,需要研究相邻两个连杆i-1和i之间的运动传递关系,如图5-11所示。

图5-11 相邻连杆的线速度和角速度关系(转动关节-转动关节)
由于连杆角速度也是向量,先分析相邻两个连杆的角速度合成问题。如图5-12所示机构,构件1和构件2做旋转运动。其中构件1相对于基座的旋转角速度向量为ωe;构件2相对于构件1的旋转角速度为ωr。根据刚体转动的角速度合成定理:构件2转动的绝对角速度ωa等于牵连角度ωe和相对角速度ωr的向量和,即
ωa=ωe+ωr(5-38)
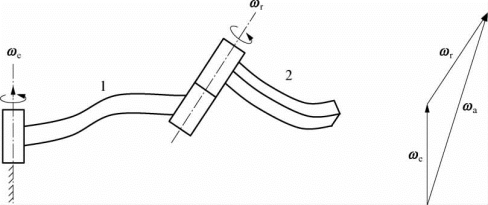
图5-12 两个刚体转动的合成
向量合成的前提是所有向量均在同一个坐标系中描述,如图5-11所示,在坐标系{i}中,连杆i+1的转动角速度ωi+1为
![]()
式中,iωi+1为在坐标系{i}中描述的连杆i+1的角速度ωi+1(绝对角速度);iωi为在坐标系{i}中描述的连杆i的角速度ωi(牵连角速度)![]() 为连杆i+1相对于关节i+1的轴线Zi+1转动的角速度大小(相对角速度大小)
为连杆i+1相对于关节i+1的轴线Zi+1转动的角速度大小(相对角速度大小)![]() 为连杆i+1相对于关节i+1的轴线Zi+1转动的角速度向量ωr在坐标系{i+1}中描述,即相对角速度向量
为连杆i+1相对于关节i+1的轴线Zi+1转动的角速度向量ωr在坐标系{i+1}中描述,即相对角速度向量![]()
![]() 为连杆i+1相对于关节i+1的轴线Zi+1转动的角速度向量ωr在坐标系{i}中描述。
为连杆i+1相对于关节i+1的轴线Zi+1转动的角速度向量ωr在坐标系{i}中描述。
式(5-39)中所的向量均为坐标系{i}中的向量,也可以将这些向量变换到坐标系{i+1}中,即将式(5-39)两边左乘![]() (坐标系{i}相对于坐标系{i+1}的姿态矩阵,因姿态矩阵是正交矩阵,故
(坐标系{i}相对于坐标系{i+1}的姿态矩阵,因姿态矩阵是正交矩阵,故![]() ,可得连杆i+1的转动角速度
,可得连杆i+1的转动角速度![]()
![]() ,因而
,因而
![]()
需要指出的是:
(1)因为同一个向量可以在任何一个坐标系中描述,因而![]() 的作用是把连杆i+1的角速度ωi+1由坐标系{i}中描述变换到坐标系{i+1}中描述;而
的作用是把连杆i+1的角速度ωi+1由坐标系{i}中描述变换到坐标系{i+1}中描述;而![]() 则是把连杆i的角速度ωi由坐标系{i}中描述变换到坐标系{i+1}中描述。
则是把连杆i的角速度ωi由坐标系{i}中描述变换到坐标系{i+1}中描述。
(2)![]() 为坐标系{i}相对于坐标系{i+1}的姿态矩阵,则
为坐标系{i}相对于坐标系{i+1}的姿态矩阵,则![]() 为坐标系{i+1}相对于坐标系{i}的姿态矩阵,它们互为逆阵,即
为坐标系{i+1}相对于坐标系{i}的姿态矩阵,它们互为逆阵,即![]() =I。
=I。
2)线速度传递
如图5-11所示,需要确定连杆i+1上的坐标系{i+1}原点Oi+1的速度v oi+1与连杆i上的坐标系{i}原点Oi的速度v oi的关系。因为坐标系{i+1}原点Oi+1通过关节i+1的旋转轴线Zi+1,因此连杆i+1绕轴线Zi+1的旋转运动不影响点Oi+1的线速度,所以只需把坐标系{i+1}原点Oi+1作为连杆i上的点,利用同一构件i上点Oi+1与Oi之间的速度合成定理:Oi+1的绝对速度v oi+1等于“基点”Oi的绝对速度v oi(牵连速度)和点Oi+1绕基点Oi的转动速度(相对速度)的向量和。同样,向量合成的前提是所有向量均在同一个坐标系中描述,因而(https://www.daowen.com)
![]()
式(5-41)中所有的向量均为坐标系{i}中的向量,也可以将这些向量变换到坐标系{i+1}中,即将式(5-41)两边左乘![]() (坐标系{i+1}相对于坐标系{i}的姿态矩阵)可得
(坐标系{i+1}相对于坐标系{i}的姿态矩阵)可得
![]()
即
![]()
当关节i+1为移动关节时,如图5-13所示,坐标系{i+1}原点Oi+1沿着关节i+1的轴线Zi+1移动,该运动影响原点Oi+1的速度,此时可以应用不同构件上点的运动关系:“原点Oi+1的绝对速度v oi+1等于牵连速度v e和相对速度v r之和”,求出坐标系{i+1}原点Oi+1的速度。
![]()
式中![]() 为牵连速度,即连杆i上与原点Oi+1“重合”的点的速度;
为牵连速度,即连杆i上与原点Oi+1“重合”的点的速度;![]() 为连杆i+1与连杆i之间的相对速度。
为连杆i+1与连杆i之间的相对速度。
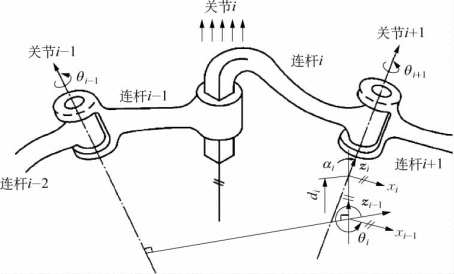
图5-13 相邻连杆的线速度和角速度关系(转动关节-移动关节)
式(5-39)和式(5-41)为连杆i+1转动角速度向量ωi和连杆上坐标系{i+1}的原点移动速度向量v oi+1在坐标系{i}中的描述;如果需要把它们变换到基坐标系{0}中描述,则分别左乘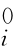 R和
R和![]() 即可,即
即可,即

说明:式(5-39)~式(5-41)是相邻连杆之间线速度和角速度关系的递推关系式。顺着运动链,应用这些表达式可以依次计算出连杆1上的坐标系{1}、连杆2上的坐标系{2}、连杆3上的坐标系{3}、……直至机器人末端连杆n上的坐标系{n}原点的线速度以及各连杆转动的角速度向量。
【例5-2】 试求图5-10所示平面2自由度机器人的速度传递关系。
解:由式(5-39)和式(5-41)可得

故姿态矩阵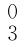 R=
R=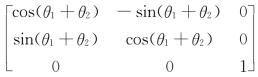 ,因而
,因而
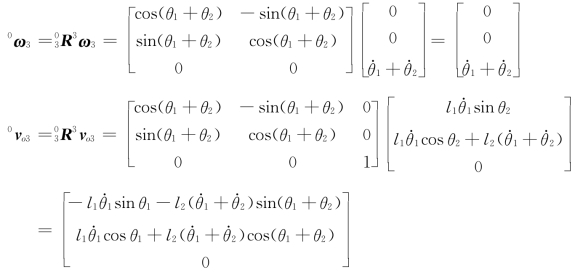
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






