由式(5-25)可知机器人工具坐标系{T}相对于基坐标系{0}的位置p T0和姿态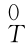 R所有关节变量θ1、θ2、…、θn的函数。由式(5-26)可知该坐标系原点的移动速度0v T和坐标系{T}相对于坐标系{0}转动角速度0ωT与所有关节速度
R所有关节变量θ1、θ2、…、θn的函数。由式(5-26)可知该坐标系原点的移动速度0v T和坐标系{T}相对于坐标系{0}转动角速度0ωT与所有关节速度 1、
1、 2、…、
2、…、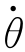 n相关,它们之间的联系称为机器人速度雅可比矩阵。关键的问题是如何确定该矩阵。
n相关,它们之间的联系称为机器人速度雅可比矩阵。关键的问题是如何确定该矩阵。
工具坐标系{T}原点相对于基坐标系{0}的线速度为0v T=[v Txv Tyv Tz]T=[p Tx,p Ty,p Tz]T,其中的p Tx、p Ty、p Tz不显含时间t,它们要对时间求全导数,可以根据多元复合函数求导法则,即先对中间变量θ1、θ2、…、θn求导,然后再由θ1、θ2、…、θn对时间t求导,因而0v T为

其中
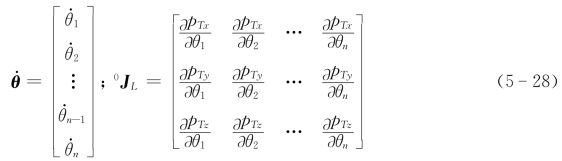
式(5-28)表明,0J L为3×n矩阵。
由于姿态矩阵的各个元素nx、ny、nz、ox、oy、oz、ax、ay、az不显含时间t,它们要对时间求全导数,可以根据多元复合函数求导法则,即先对中间变量θ1、θ2、…、θn求导,然后再由θ1、θ2、…、θn对时间t求导,因此,由式(5-19)可得工具坐标系{T}相对于基坐标系{0}的转动角度0ωT为
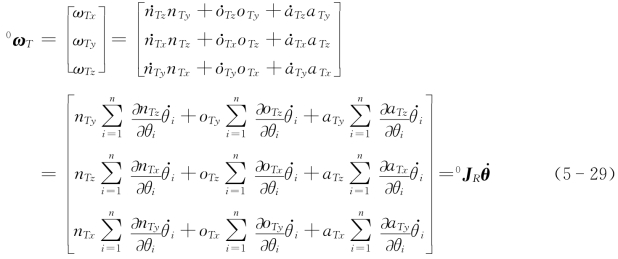
其中
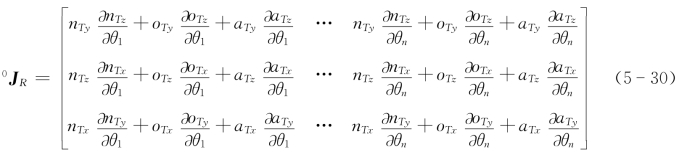
式(5-30)表明,0J R为3×n矩阵。
将式(5-27)和式(5-29)合并可得
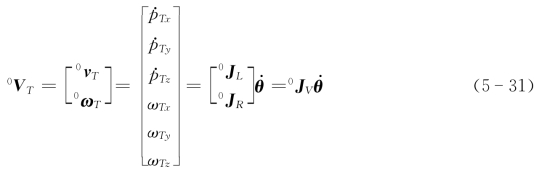
其中
![]()
式(5-32)表明,0J V为6×n矩阵。
式(5-31)建立了机器人工具坐标系{T}的速度(包括线速度和角速度)与机器人各连杆速度的关系,式中的6×n矩阵0J V称为在基坐标系{0}中的机器人速度雅可比矩阵。
当然,因为式(5-31)中机器人末端执行器的速度向量是在基坐标系{0}中描述的,当机器人工具坐标系{T}速度在其他坐标系连杆k的坐标系{k}中定义时,雅可比矩阵的表达式kJ V不同。根据式(2-12)所示的向量在两个坐标系之间的转换关系,机器人工具坐标系{T}的速度在任意两个连杆坐标系{k}和{l}之间的变换关系为
![]()
因为kV T=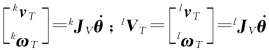 ,故
,故
![]()
从而可得
![]()
由式(5-32)可知,对于一个n自由度机器空间人,其雅可比矩阵为6×n矩阵。通用机器人一般有6个自由度,其雅可比矩阵0J V为6×6方阵。如果方阵0J V可逆,设其逆阵为0J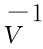 ,则利用式(5-31)可以求出机器人的关节速度[
,则利用式(5-31)可以求出机器人的关节速度[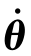 =
= 1
1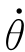 2…
2…  6]T与末端执行器的速度0V T=[
6]T与末端执行器的速度0V T=[ Tx
Tx Ty
Ty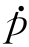 TzωTxωTyωTz]T的关系为
TzωTxωTyωTz]T的关系为

如果机器人的运动受到约束,如平面机器人,其构件在同一平面或者平行平面内运动,则末端执行器的速度向量0v T少于6行。设机器人所在直角坐标空间有m个自由度,机器人有n个独立关节,则其雅可比矩阵0J V为m×n矩阵,记为0J Vm×n。因此,雅可比矩阵的“行数”就是机器人所在直角坐标空间的自由度数,“列数”就是机器人独立关节的数目。
由式(5-28)和式(5-30)可知,机器人速度雅可比矩阵0J V仅仅是关节变量θ=[θ1θ2… θn]T的函数,即机器人位置的函数,记为0J V(θ)。对于机器人工作空间内的不同位置θ,速度雅可比矩阵0J V(θ)m×n的秩Rank[0J V(θ)m×n](不为0的最大余子式的行列式的阶数)可能不同,设其最大值K=max Rank[0J V(θ)m×n]。若在某位置θi=[θi1θi2… θin]T,雅可比矩阵0J V(θi)m×n的秩Rank[0J V(θi)m×n]<K;则称机器人处于“奇异位姿”或“奇异状态”。
一般机器人都有“奇异位姿”。所有的工业机器人在其工作空间的边界都存在“奇异位姿”,此时机器人位于所有关节全部展开或者收回的状态,如图5-8所示是平面2自由度机器人在工作空间边界点的奇异位姿。大部分工业机器人在其工作空间内也存在“奇异位姿”,此时有两个或多个关节轴共线,如图5-9所示。
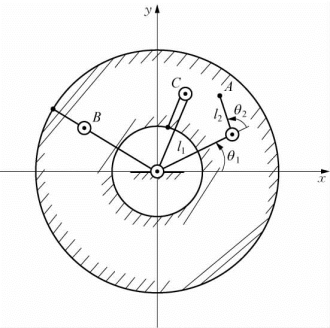
图5-8 平面2自由度机器人关节展开时的奇异位姿

图5-9 关节机器人关节轴线共线时的奇异位姿
当机器人处于奇异位姿时,它会失去一个或多个自由度,某些关节角速度趋近无穷大。在直角坐标空间的某些方向上,无论关节速度有多大,都不能使机器人手臂沿该方向移动。
当雅可比矩阵0J V为方阵时,即0J V(θ)n×n,若θi=[θi1θi2… θin]T,行列式det0[J V(θi)n×n]=0,称机器人在θi处于“奇异位姿”或“奇异状态”。以通用工业机器人为例,因n=6,可以令det[0J V(θ)6×6]=0便可以确定机器人的所有奇异位姿。在规划机器人的运动轨迹时,要避开奇异位姿。
与机器人速度雅可比矩阵相关问题有三类:正向问题、逆向问题和机器人末端执行器位姿微调问题。(https://www.daowen.com)
(1)正向问题。已知机器人各连杆速度 =[
=[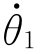
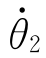 …
… 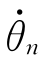 ]的情况下,求机器人末端连杆(或末端执行器)的线速度0v T(坐标系原点)和转动角速度0ωT。
]的情况下,求机器人末端连杆(或末端执行器)的线速度0v T(坐标系原点)和转动角速度0ωT。
(2)逆向问题。已知机器人末端连杆(或末端执行器)的线速度0v T(坐标系原点)和转动角速度0ωT的情况下求机器人各连杆速度 =[
=[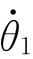
 …
…  ]T。
]T。
(3)末端执行器位置和姿态微调整问题。对于工件装配作业、工件抓取、焊接作业等,有时要求末端执行器相对于当前的位置和姿态做“微小调整”,以满足作业要求。此时需要确定各关节的微小位移量Δθ=[Δθ1Δθ2… Δθn]T。
第一类问题(正向问题)求解方法:只要求出当前时刻机器人的雅可比矩阵0J V,并把0J V和关节速度 =[
=[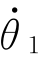
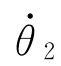 …
…  ]代入式(5-31)即可解决。
]代入式(5-31)即可解决。
第二类问题(逆向问题)求解方法:由于式(5-31)中的雅可比矩阵0J V、线速度0v T和转动角速度0ωT均为已知量,要确定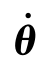 =[
=[
 …
… 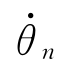 ],这就变成了如下代数方程组求解的问题
],这就变成了如下代数方程组求解的问题

上述方程组是否有解与雅可比矩阵0J V的“秩”有关(秩是线性代数中概念,一个m行n列矩阵A m×n就是m个行向量或n个列向量中最大线性无关组的个数)。根据线性方程组有解的充分必要条件是:系数矩阵0J V的“秩”Rank(0J V)和增广矩阵[0J V0V T]的秩Rank([J VV])相等,即Rank(0J V)=Rank([0J V0V T]),否则线性代数方程组(5-35)无解。
若式(5-35)出现“无解”情况,意味着在机器人末端连杆(末端执行器)在工作空间的某个位置,其指定的速度V=[p·xp·yp·zωxωyωz]T机器人无法实现。
一般的代数方程组有规范的求解方法,即通过对增广矩阵进行初等行变换,获得“阶梯矩阵”(最简行矩阵),就可以判断方程组是否有解以及解的结构,具体方法可以参考线性代数教材。
第三类问题求解方法:根据导数的定义,式(5-31)可写成0V T=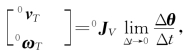 当Δt很小时
当Δt很小时

式(5-36)表明:机器人末端执行器的“微分运动”与各关节做“微分运动”之间通过速度雅可比矩阵联系起来。因此,如果给定机器人末端执行器的“微分运动”Δd=[Δp xΔpyΔpzΔα Δβ Δγ]T,通过解如下数方程组(方法同上述第二类问题求解方法),即可确定机器人各关节的“微分运动”Δθ=[Δθ1Δθ2… Δθn]T。

上述方法对于机器人末端的精细化作业,如零件精密装配、精密测量时末端执行器的微调十分有效。
【例5-1】 试求如图5-10所示平面2自由度机器人的速度雅可比矩阵。

图5-10 平面2自由度机器人
解:机器人的D-H参数见表5-1。
表5-1 平面2自由度机器人D-H参数

将上述参数代入式(3-1)可得

将上述三个矩阵代入式(5-25)可得
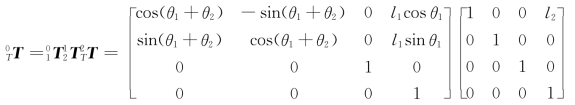

p Tx=l 2cos(θ1+θ2)+l 1cosθ1n Tx=cos(θ1+θ2)o Tx=-sin(θ1+θ2)a Tx=0
p Ty=l 2sin(θ1+θ2)+l 1sinθ1;n Ty=sin(θ1+θ2);o Ty=cos(θ1+θ2);a Ty=0
p Tz=0n Tz=0o Tz=0a Tz=1
将p Tx、p Ty、p Tz代入式(5-28)和式(5-30)可得
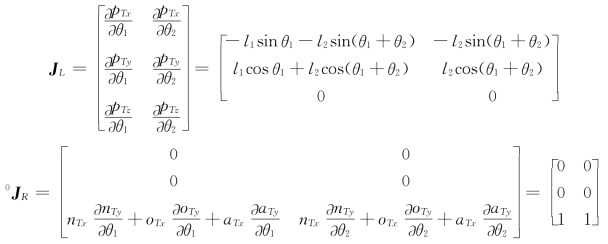
由式(5-32)可得
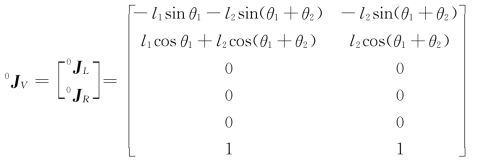
因为该机构在基坐标系中的xOy平面内运动,可以将上式简写为
![]()
利用上述二阶方阵的行列式det(0J V)=0可以求出该机器人的奇异位姿为θ2=kπ,k∈Z;即连杆1和连杆2共线时,机器人处于奇异位姿。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






