按照矩阵求导定义，每个元素都对时间t求导，则

依据式（5-12）可得

将式（5-16）代入式（5-15）可得

式（5-17）也可以参照上述求“向量”导数的方法，利用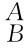R对时间求导的定义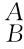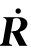＝求得。

因为矩阵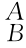R是正交矩阵，其逆矩阵等于其转置矩阵，即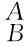R－1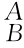＝R T，式（5-17）两边同时右乘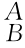R T可得

由上式可以求出角速度Aω＝［AωxAωyAωz］T＝的具体表达式。因为

由上式可得(www.daowen.com)

因为k＝［kxkykz］T是单位向量，即‖k‖＝＝1，式（5-19）中的三个等式两边分别平方，再相加可得

故旋转角速度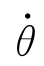为

将式（5-20）代入式（5-19）得刚体瞬时转动轴k＝［kxkykz］T，其中

由式（5-21）仅能确定刚体瞬时转动轴线l的方向，而旋转轴线的具体位置则可以利用式（2-47）确定。

式（5-18）或式（5-19）提供了一种求机器人任意连杆i瞬时转动角速度向量的有效方法。这是因为对于一个n自由度机器人，由式（3-4）可确定其任意连杆i在t时刻相对于机器人基坐标系｛0｝的位姿矩阵为；将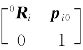中的Ri及其导数代入式（5-18），可求得连杆i相对于机器人基坐标系｛0｝转动的角速度向量Aωi＝0ωi。