基于反对称矩阵可以计算如图5-2所示的坐标系｛A｝中的自由向量Al＝lxi＋l yj＋lzk对时间的导数与刚体转动角速度的关系。

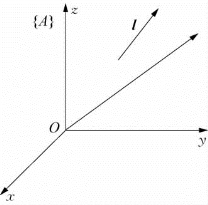
图5-2　空间中的自由向量l

按照向量对时间求导的定义可知

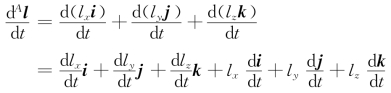
因为坐标系｛A｝中基向量i、j和k都是常向量，其导数为0向量，故上式可简化为

当向量Al＝lxi＋lyj＋lzk为常向量时，即lx、ly和l z分别为常数时，其导数都为0，故＝0。

如图5-3所示，刚体在坐标系｛A｝中做平动，刚体上任意两点Q1、Q2的向量Al＝Q1Q2在运动过程中始终与初始位置平行；因为刚体上任意两点Q1和Q2之间的距离保持不变，因而向量Al＝Q1Q2为常向量，故d Al／d t＝0。即刚体做平动时，其上任意一个向量的导数均为0向量。这表明，当刚体做一般运动时，其“平动部分”不影响刚体上向量的导数。

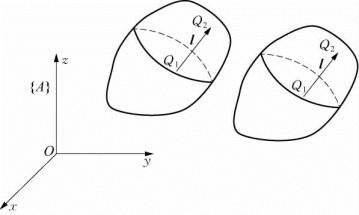
图5-3　刚体平动

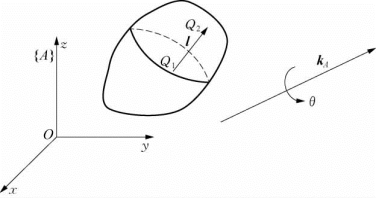
图5-4　刚体绕瞬时轴k A转动

如图5-4所示，刚体绕轴坐标系｛A｝中的k A轴转动，设为k A＝kxi＋kyj＋kzk为单位向量。设Δt时间内刚体旋转了角度Δθ，则根据第二章式（2-38），相应的旋转矩阵R kA（Δθ）为

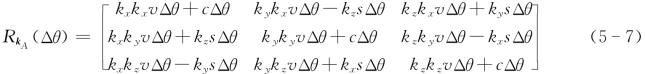
其中

cΔθ＝cosΔθ；sΔθ＝sinΔθ；vΔθ＝1－cosΔθ

经过上述则旋转后向量l变为：Al（t＋Δt）＝R kA（Δθ）Al。(www.daowen.com)

按照向量导数定义：

当Δt很小时，Δθ也很小，此时：（1－cosΔθ）≈0；cos（Δθ）≈1；sinΔθ≈Δθ，则

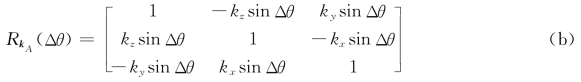
将式（b）代入式（a）可得

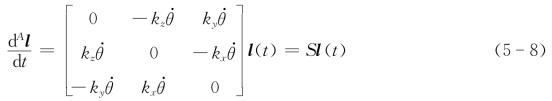
其中

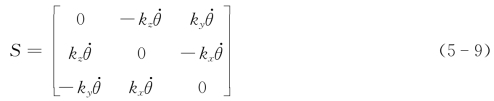
此时刚体相对于坐标系｛A｝转动的角速度大小为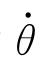，角速度向量Aω的方向可以按照“右手定则（右手四指绕向转方动方向，拇指的指向即为角速度向量的方向）”确定，即Aω与向量k的方向一致，如图5-4所示；根据向量等于向量的模与单位向量的积，故Aω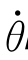＝k，从而可以确定Aω在坐标系｛A｝上三个坐标轴的坐标（投影）为

依据式（5-3），向量Aω＝对应的反对称矩阵为

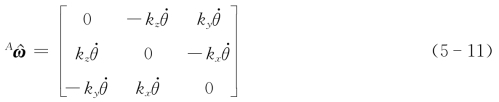
称向量Aω＝的反对称矩阵A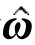为角速度张量。

对比式（5-9）和式（5-11）可知：S＝ω，故结合式（5-5）可得

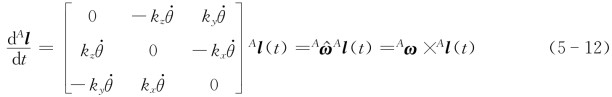
由式（5-12）可以得出的结论是：坐标系｛A｝中任一自由向量Al对时间的导数，等于该向量（随刚体）转动的角速度向量Aω与其自身Al的“叉积”。

由于刚体转动的角速度是向量，其坐标依赖于“基坐标系”的选取，因此在描述刚体转动的角速度向量时应该指明在哪个坐标系中的角速度向量。

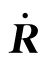在应用式（5-12）研究坐标系｛A｝中的向量Al对时间的导数时，关键的问题是如何确定向量（刚体）转动的角速度向量Aω。由于姿态矩阵R是反映刚体与参考坐标系之间的方向（角度）关系，其导数能够反映刚体转动的快慢，因此，可以利用确定刚体在坐标系｛A｝中转动的角速度向量Aω。