工作台坐标系｛S｝是为了便于描述工件运动轨迹设定的坐标系，但是机器人的运动指令都是以机器人基坐标系｛B｝为基准给出的，因而需要把该运动轨迹通过工作台坐标系｛S｝与机器人基坐标系｛B｝的关系转换到基坐标系中。如果工作台坐标系｛S｝与机器人基坐标系｛B｝之间的关系建立的不准确，或者由于外在原因（如工作台发生偏移），这都会使它们之间的关系发生变化，都会导致机器人末端执行器的“真实运动轨迹”偏离“目标轨迹”，因而也需要进行标定。

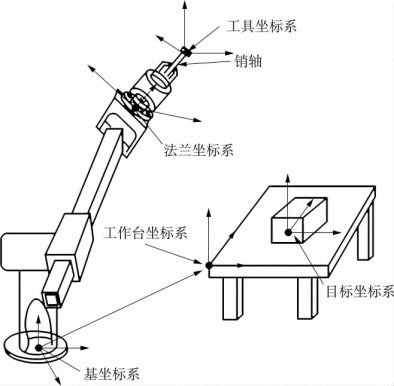
图4-7　与机器人作业相关的坐标系

如图4-7所示，机器人及外围设备在现场安装完毕之后，在投入运行前，应对机器人进行标定，目的是修正机器人的位姿精度，并建立机器人基坐标系、工件坐标系、工作台坐标系、世界坐标系和工具坐标系之间的准确关系。否则，机器人无法完成规划的运动轨迹。

1）零点校正

按照机器人使用说明书的具体要求，参照4.3.1节的方法，用测量仪器或千分尺标定机器人每一个轴的“零点”。

2）机器人位姿和轨迹标定

按照机器人使用说明书的具体要求，参照本书4.3.2～4.3.4节的方法，完成机器人位置精度、姿态精度和轨迹精度的标定。

3）设定工具坐标系TCS

工具坐标系是指在机器人末端执行器上建立的坐标系，是为了便于控制末端执行器与作业对象之间的运动而建立的。机器人工具坐标系TCS由工具中心点（tool center point，TCP）与坐标方位组成。机器人完成作业任务时，TCP是必需的，如图4-8所示。

图4-8　机器人工具坐标系

由于工具安装在机器人末端连杆的法兰上，工具坐标系的标定，就是建立工具坐标系相对于法兰坐标系的位姿关系，如图4-9所示。

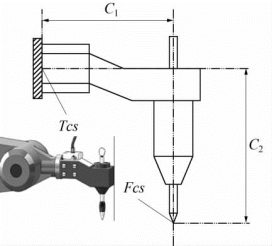
图4-9　机器人工具坐标系与法兰坐标系的关系

图4-10　机器人工具坐标系的标定

通过选定一系列工具坐标系的典型位姿，如图4-10所示，由系统自动确定工具坐标系｛T｝与机器人末端法兰之间的位姿关系。

常用的方法包括：

（1）N（N≥4）点法。机器TCP通过N种不同姿态同某定点相碰，得出多组解，通过计算得出当前TCP与机器人法兰中心点相应位置，坐标系方向与法兰坐标系一致。

（2）TCP ＆ Z法。在N点法基础上，Z点与定点连线为坐标系Z方向。

（3）TCP ＆ X、Z法。在N点法基础上，X点与定点连线为坐标系X方向，Z点与定点连线为坐标系Z方向。

上述方法可以建立工具坐标系与法兰坐标系之间的位姿关系，但其标定原理需要研究。

机器人运动学方程建立了机器人末端连杆坐标系与机器人基坐标系之间的关系。机器人末端连杆上有法兰，用于连接末端执行器；机器人制造商在末端法兰上建立了一个坐标系，这个法兰坐标系与机器人末端连杆坐标系之间的位置和姿态是确定的；机器人工具坐标系建立在机器人末端执行器上，而末端执行器是通过机器人末端连杆上的法兰与末端连杆固接在一起。只要建立工具坐标系与法兰坐标系之间的关系，就可以确定机器人工具坐标系与机器人基坐标系之间的关系。这种关系可以通过“标定”来实现。

一般商用机器人都提供其机器人工具坐标系的标定方法，所谓工具坐标系的标定，就是要确定机器人工具坐标系｛T｝和机器人末端连杆坐标系｛n｝之间的位姿关系，即

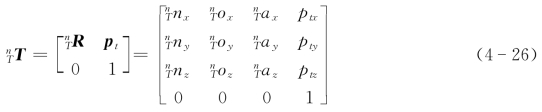
式中，p t＝［ptxptyptz］T为工具坐标系｛T｝的原点在末端连杆坐标系｛n｝中的位置向量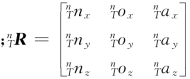为工具坐标系｛T｝的原点在末端连杆坐标系｛n｝中的姿态。

一旦标定完毕，工具坐标系｛T｝和机器人末端连杆坐标系｛n｝之间的位姿矩阵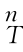T保持不变。

4）设定工作台坐标系｛S｝和世界坐标系｛Wo｝

为了便于描述工件的运动（作业）而在机器人工作台选定位置设立的坐标系，称为工作台坐标系或者用户坐标系。(www.daowen.com)

一般商用机器人都提供其机器人工作台坐标系｛S｝的建立及标定方法。所谓工作台坐标系的标定，就是要确定工作台坐标系｛S｝和机器人基坐标系｛0｝之间的位姿关系。

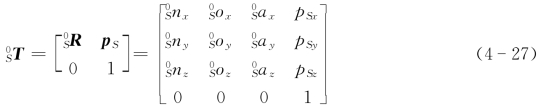
式中，p S＝（p Sxp Syp Sz）T为工作台坐标系｛S｝的原点在机器人基坐标系｛0｝中的位置向量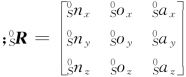为工作台坐标系｛S｝在基坐标系｛0｝中的姿态。

一旦标定完毕，工作台坐标系｛S｝和机器人基坐标系｛0｝之间的位姿矩阵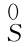T保持不变。

当要控制两个及两个以上的机器人协调工作时，需要设定世界坐标系｛Wo｝，其设定方法与上述方法类似。

5）设定目标坐标系（工件坐标系）｛G｝

目标坐标系｛G｝是为了描述工件（刚体）在空间中的运动，即位姿变化，而在工件上建立的与工件“固定连接”的坐标系。

每种商用机器人都有其设定目标坐标系的方法，一般通过一系列规定的位姿进行标定，具体方式可以参考机器人使用说明书。

6）目标坐标系（工件坐标系）｛G｝与工作台坐标系｛S｝之间关系的建立及标定

工件的运动一般在工作台坐标系｛S｝中描述，包括位姿和姿态变化SGT，如焊接作业时焊缝的轨迹，搬运作业时工件的初始位置和终了位置都在工作台坐标系中描述。为了让机器人末端执行器能够精确完成作业任务，需要确定工件相对于机器人基坐标系｛0｝的位置和姿态，为此可通过坐标变换完成

在此基础上，才能应用轨迹规划的方法，完成机器人末端执行器作业的运动规划。

参考文献

［1］Craig JJ．Introduction to robotics mechanics and control［M］．3rd ed．［S．l．］：Person Education，Inc．Published as Prentice Hall，2005．

［2］Niku S B．Introduction to robotics：analysis，control，applications［M］．2nd ed．［S．l．］：John Wiley ＆ Sons，Inc．，2010．

［3］Murray R M，Li Z X，Sastry SS．A mathematical introduction to robotic manipulator［M］．［S．l．］：CRC Press，1994．

［4］肖尚彬．元数方法及其应用［J］．力学进展，1993，23（2）：249-260．

［5］熊有伦．机器人技术基础［M］．武汉：华中科技大学出版社，2004．

［6］宋伟刚．机器人学：运动学、动力学与控制［M］．北京：科学出版社，2007．

［7］孙树栋．工业机器人技术基础［M］．西安：西北工业大学出版社，2006．

［8］ISO 9283：1998 Manipulating industrial robots-performance criteria and related test methods．

［9］GB／T 12642—2013　工业机器人性能规范及其试验方法．

［10］Hayati S，Mirmirani M．Improving the absolute positioning accuracy of robot manipulators［J］．Journal of Field Robotics，1985，2（4）：397-413．

思考与练习

1.试求如图3-17所示3自由度机器人的逆向运动学问题。

2.试求如图3-18所示SCARA机器人的逆向运动学问题。

3.试求如图3-19所示肘关节机器人的逆向运动学问题。

4.试求如图3-20所示机器人的逆向运动学问题。

5.试求如图3-21所示机器人的逆向运动学问题。