【实例1：KUKA机器人逆向运动学求解】

试求解如图3-9所示KUKA KR6-900机器人的逆向运动学。

解：由式（3-4）可知

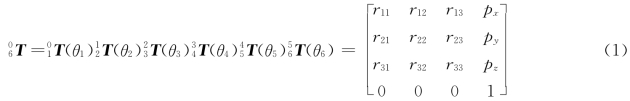
其中

r11＝c1［c23（c4c5c6－s4s5）－s23s5c5］＋s1（s4c5c6＋c4s6）

r21＝s1［c23（c4c5c6－s4s6）－s23s5c6］－c1（s4c5c6＋c4s6）

r31＝－s23（c4c5c6－s4s6）－c23s5c6

r12＝c1［c23（－c4c5c6－s4c6）＋s23s5c6］＋s1（c4c6－s4c 5s6）

r22＝s1［c23（－c4c5c6－s4c6）＋s23s5c6］－c1（c4c6－s4c5s6）

r32＝－s23（－c4c5c6－s4c6）＋s23s5s6

r13＝－c1（c23c4c5＋s23c5）－s1s4s5

r23＝－s1（c23c4c5＋s23c5）＋c1s4s5

r33＝－s23c4c5＋c23c5

p x＝c1（a2c2＋a3c23－d 4s23）－d 3s1

p y＝s1（a2c2＋a3c23－d 4s23）＋d 3c1

pz＝－a2s23－a2s2－d 4c23

式中，ci＝cosθi，si＝sinθi，cij＝cos（θi＋θj），sij＝sin（θi＋θj）。

1）求θ1

用［01T（θ1）］－1去乘式（1）两端可得

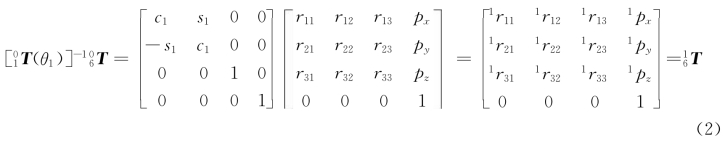
其中

1r11＝c23（c4c5c6－s4s6）－s23s5c6

1r21＝－s4c5c6－c4s6

1r31＝－s23（c4c5c6－s4s6）－c23s5c6

1r12＝－c23（c4c5c6＋s4s6）＋s23s5s6

1r22＝s4c5s6－c4c6

1r32＝s23（c4c5c6＋s4c6）＋c23s5s6

1r13＝－c23c4s5－s23c5

1r23＝s4s5

1r33＝s23c4s5－c23c5

1p x＝a2c2＋a3c23－d 4s23

1py＝d 3

1pz＝－a3s23－a2s2－d 4c23

令式（2）两端元素（2，4）（第二行第四列元素）相等，可得

－s1px＋c1p 2＝d 3　（3）

令：p x＝ρcosφ；py＝ρsinφ，其中ρ＝；φ＝a tan 2（px，py），代入式（3）可得：sin（φ－θ1）＝；cos（φ－θ1）＝±，利用反正切函数a tan2（y，x）可得：φ－θ1＝a tan 2，故

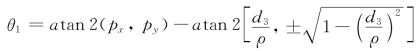
2）求θ3

令式（2）两端元素（1，4）、元素（3，4）分别相等，可得以下两个有效的三角方程

将上两式两边平方并相加得

a3c3－d 4s3＝k　（5）

其中

由式（5）可得

3）求解θ2

为求解θ2，在式（1）两端左乘逆变换矩阵T－1可得

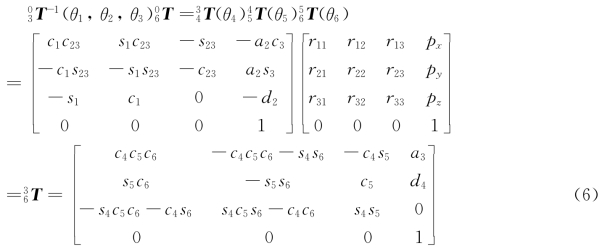
令式（6）两边元素（1，4）和元素（2，4）分别相等，可得

由式（7）可解得

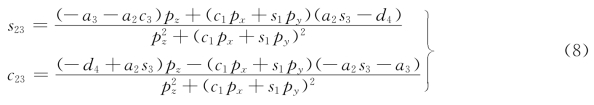
式（8）中s23和c23分母相等，且为正，用利用反正切函数a tan 2（y，x）可得

θ23＝θ2＋θ3＝a tan 2（s23，c23）

根据θ2和θ3的四种可能组合，可以由上式求得四种可能的θ23

θ2＝θ23－θ3

4）求θ4

由于θ2和θ3已知，式（6）中元素都为已知数，令其两边元素（1，3）和元素（3，3）分别对应相等，可得

只要s5≠0，就可以求得

θ4＝a tan 2（－r13s1＋r23c1，－r13s1c23－r23s1c23＋r33s23）

当s5＝0时，机器人处于奇异位姿，产生了退化。此时关节轴4和轴6重合，只能解出θ4和θ6的和或差。奇异位姿可以由θ4的结果判断，当两个变量都为0则为奇异位姿。

5）求θ5

在式（1）两端左乘逆变换矩阵T－1（θ1，θ2，θ3，θ4）可得

其中θ1，θ2，θ3，θ4均已解出，故

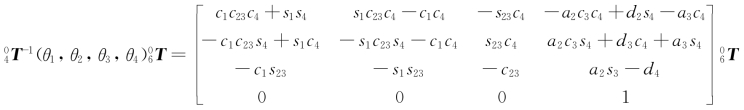
即

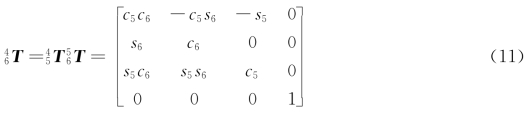
令式（11）两边元素（1，3）和元素（3，3）分别相等，可得

由式（12）可得

θ5＝a tan 2（s5，c5）

6）求θ6

在式（1）两端左乘逆变换矩阵T－1（θ1，θ2，θ3，θ4，θ5）可得

令式（13）两边元素（3，1）和元素（1，1）分别相等，可得

－r11（c1c23s4－s1c4）－r12（s1c23s4＋c1c4）＋r13（s23s4）＝s6

r11［（c1c23c4＋s1s4）c5－c1s23s4］＋r12［（s1c23c4－c1s4）c5－s1s23s5］－r13（s23c4c5＋c23s4）＝c6

联立上式可以求得

θ6＝a tan 2（s6，c6）

至此，该机器人的逆向运动学问题得以解决，逆向运动共有8种可能的反解。当计算出所有的8种解后，可以根据关节变量的运动范围、运动的连续性以及避障要求剔除多余的解。(www.daowen.com)

【实例2：ABB机器人逆向运动学求解】

试求解如图3-11所示的ABB IRB 120机器人的逆向运动学。

解：由式（3-3）可得

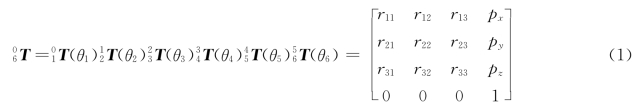
其中

r11＝c1［c23（c4c5c6－s4s6）－s23s5c6］＋s1（s4c5c6＋c4s6）

r12＝c1［c23（－c4c5s6－s4c6）＋s23s5s6］＋s1（c4c6－s4c5s6）

r13＝－c1［s23c5＋c23c4s5］－s1s4s5

r21＝s1［c23（c4c5c6－s4s6）－s23s5c6］－c1（c4s6＋s4c5c6）

r22＝s1［c23（－c4c5s6－s4c6）＋s23s5s6］－c1（c4c6－s4c5s6）

r23＝c1s4s5－s1（c5s23＋c4s5c23）

r31＝s23（s4s6－c4c5c6）－c23s5c6

r32＝s23（s4c6＋c4c5s6）＋c23s5s6

r33＝s23c4s5－c23c5

p x＝－s1d 2＋c1（c23a3－s23d 4＋a2c2）

p y＝c1d 2＋s1（c23a3－s23d 4＋a2c2）

p z＝－s23a3－c23d 4－a2s2

式中，ci＝cosθi，si＝sinθi，cij＝cos（θi＋θj），sij＝sin（θi＋θj）。

1）求θ1

用［T（θ1）］－1去乘式（1）两边可得

［，即

令矩阵（2）两边的元素（2，4）相等，可得，故

－s1px＋c1py＝d 2　（3）

令

由式（3）可得：sin（φ－θ1）＝

则

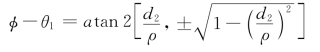
从而

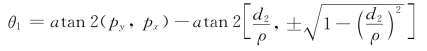
由上式可以看出，θ1可以有两种解。

2）求θ3

至此，θ1已知，则式（2）左边都为已知。如果令式（2）两边的元素（1，4）和元素（3，4）分别相等，得

将式（4）平方并相加可得

a3c3－d 4s3＝k　（5）

其中

由式（5）可以解出θ3为

式中的“±”号使得θ3有两个不同的解。

3）求θ2

重新调整式（2），使公式左边只有θ2和已知函数，则

即

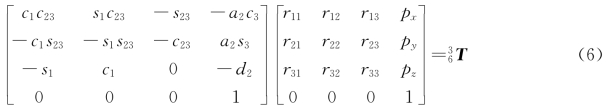
式（6）中：T由正向运动学已确定。令式（6）两边的元素（1，4）和元素（2，4）分别相等，可得

由式（7）可以解出s23和c23

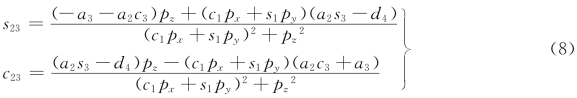
式（8）中分母相等，所以可以求得θ2和θ3的和为

θ23＝a tan 2（s23，c23）

根据θ1和θ3的4种可能组合，由上式计算θ23的4个值，然后计算θ2的4个可能的解。

θ2＝θ23－θ3

上式中应针对不同的情况选取θ3。

4）求θ4

由于式（6）中的左边完全已知，令式（6）两边的元素（1，3）和元素（3，3）分别相等，可得

只要s5≠0，就可以由式（9）解出θ4

θ4＝a tan 2（－s1r13＋c1r23，－c1c23r13－s1c23r23＋s23r33）

当θ5＝0时，机器人处于奇异形，此时关节轴4和轴6呈一条直线，机器人末端连杆的运动只有一种。在这种情况下，所有可能的解都是θ4和θ6的和或差。这种情况可以通过检查式（12）中a tan 2的两个变量是否都趋近于零来判断。如果都趋近于零，则θ4可以任意选取，之后计算θ6时，可以参照θ4进行选取。

5）求θ5

改写正向运动学方程式，使公式左边均为已知数和θ4，即

其中

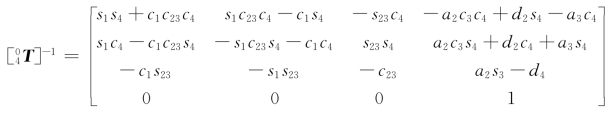
T由前式已得到。令式（10）两边的元素（1，3）和元素（3，3）分别相等，得

由式（11）可以解出θ5为

θ5＝a tan 2（s5，c5）

6）求θ6

同理，计算出［T］－1，并改写正运动学方程为如下形式：

令式（12）左右两边元素（1，1）和元素（3，1）分别相等，可得

θ6＝a tan 2（s6，c6）

其中

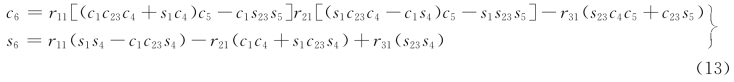
由于θ1和θ3的表达式中出现了“±”号，因此这些方程可能有4种解。另外机器人可以进行关节“翻转”得到另外4个解：

θ′4＝θ4＋180°

θ′5＝－θ5

θ′6＝θ6＋180°

当计算出所有的8种解后，可以根据关节变量的运动范围、运动的连续性以及避障要求剔除多余的解。