对于工业机器人，其逆向运动学求解方法中最常用的是利用矩阵变换的方法以及基于旋量的方法。本节采用矩阵变换的方法，即利用位姿矩阵的逆矩阵对运动学方程实施变换，以期获得关于机器人关节变量的有效三角方程（方程组）。其具体步骤如下：

（1）分别用D-H矩阵的逆矩阵或逆矩阵的组合：（1≤i≤n）去乘式（4-1）所示的机器人运动学方程的两端，从而得到以下n个方程：

（2）比较矩阵方程（4-5）两边的对应元素，以期得到尽可能多的有效的三角方程（即可以解出单个关节变量的方程或方程组）。求解这些三角方程，以求得某些关节变量的解析表达式。

（3）对于那些尚不能确定的关节变量，则需要利用方程（4-6）～方程（4-8），通过比较这些矩阵方程两边对应元素而获得有效的三角方程，再由这些三角方程求解这些关节变量，直至求解出所有关节变量。

在上述求解过程中，常见的有效三角方程主要包括下面三种类型：

lixsinθi＋liycosθi＝di　（4-9）

式中，lix、liy、di、l 1x、l 1y、l 2x、l 2y、d 1、d 2分别为常数。(www.daowen.com)

对于上述三类方程，可以利用三角恒等变换求出关节变量θi或θj。

求解机器人逆向运动学问题应该注意以下几点：

（1）在利用三角函数方程求解关节变量时，应充分利用反正切函数

αi＝a tan 2（yi，xi）（αi∈［－π，π］）　（4-12）

该函数在［－π，π］范围内精度均匀，并能根据yi／xi的值以及y i和x i的正负号确定αi的值及所在的象限，如图4-2所示。

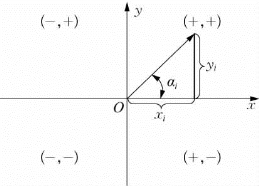
图4-2　反正切函数α＝a tan 2（y，x）

（2）机构奇异性问题。所谓机构奇异性，是指机器人处于某些位姿时，其雅可比矩阵的秩减小。如果能确定使得雅可比矩阵“降秩”的某些关节角的值，在求解逆向运动学问题时可以以这些值为分界点进行讨论，以便于确定其余的关节变量。具体而言，就是在求得关节变量αi＝a tan 2（yi，xi）时，应讨论yi和x i同时为0的情况。

（3）逆向运动学求解过程中会出现多解问题。此时可以基于机器人各关节的运动范围、运动的连续性以及避障要求剔除多余的解。