对于一个n自由度机器人，其逆向运动学，就是在机器人末端执行器的位姿矩阵给定的情况下，确定每个关节的运动角度θ＝［θ1θ2…　θn］T。为解决这个问题，需要应用式（3-3）所示的机器人正向运动学方程，但机器人运动学方程一般给出的是机器人末端连杆坐标系｛n｝相对于机器人基坐标系｛0｝的位姿。为了求出机器人的关节变量θ＝［θ1θ2…　θn］T，可以按以下两步进行：

1）根据指定的机器人末端执行器的位姿T，确定机器人末端连杆的位姿矩阵T

由于机器人作业时，工具坐标系（末端执行器坐标系）｛T｝的位姿才是机器人工作所需要的位姿，而工具坐标系“固定”在机器人末端连杆n的法兰盘上，如图4-1所示。接下来需要解决的问题是，如何由工具坐标系的位姿求出末端连杆坐标系｛n｝的位姿。

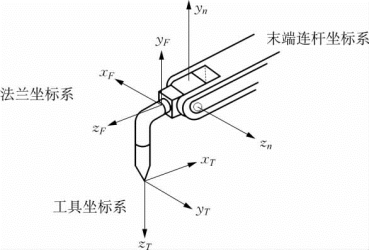
图4-1　工具坐标系与末端连杆坐标系的关系

如图4-1所示，设法兰坐标系｛F｝相对于末端连杆坐标系｛n｝的位姿为T，该位姿由机器人出厂时给定，设机器人经过标定后与法兰坐标系的位姿为T，则工具坐标系相对于末端连杆坐标系｛n｝的位姿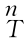T为

当根据作业要求指定了机器人工具坐标系｛T｝的位姿为T后，因为机器人末端连杆坐标系｛n｝相对于机器人基坐标系｛0｝的位姿为T，而工具坐标系相对于末端连杆坐标系｛n｝的位姿为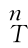T，则依据式（2-21）可得

由式（4-2）可以求得

式中，T－1为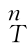T的逆矩阵，可根据式（2-20）确定。

2）根据机器人末端连杆的位姿T求解关节变量θ＝［θ1，θ2，…，θn］T

对于机器人运动学方程式（3-3），由于右端g＝T已知，需要确定机器人所有关节变量θ＝［θ1θ2…　θn］T的值。根据式（3-3）可得

其中

r11＝r11（θ1，θ2，…，θn）；r12＝r12（θ1，θ2，…，θn）；r13＝r13（θ1，θ2，…，θn）；px＝px（θ1，θ2，…，θn）

r21＝r21（θ1，θ2，…，θn）；r22＝r22（θ1，θ2，…，θn）；r23＝r23（θ1，θ2，…，θn）；py＝py（θ1，θ2，…，θn）

r31＝r31（θ1，θ2，…，θn）；r32＝r32（θ1，θ2，…，θn）；r33＝r33（θ1，θ2，…，θn）；pz＝pz（θ1，θ2，…，θn）(www.daowen.com)

由于末端连杆的位姿已经由式（4-3）确定，因而nx，ny，nz；ox，oy，oz；ax，ay，az；dx，dy，dz均为已知量。

由“两个矩阵相等，则矩阵对应元素分别相等”，可以得到如下12个方程：

nx＝r11（θ1，θ2，…，θn）；ox＝r12（θ1，θ2，…，θn）；

ax＝r13（θ1，θ2，…，θn）；dx＝px（θ1，θ2，…，θn）

ny＝r21（θ1，θ2，…，θn）；oy＝r22（θ1，θ2，…，θn）；

ay＝r23（θ1，θ2，…，θn）；d y＝py（θ1，θ2，…，θn）

nz＝r31（θ1，θ2，…，θn）；oz＝r32（θ1，θ2，…，θn）；

az＝r33（θ1，θ2，…，θn）；dz＝pz（θ1，θ2，…，θn）

上述12个方程一般为非线性超越方程（含有关节变量的三角函数），同时，由于姿态矩阵的9个元素nx、ny、nz、ox、oy、oz、ax、ay、az中只有3个元素相互独立（因为a＝n×o），再加上3个相互独立的位置坐标方程，共有6个独立方程，因此求解这6个非线性超越方程较为困难，目前尚没有通用的求解方法。

当机器人自由度大于6，即独立的关节变量大于6时，自变量的个数大于独立方程的个数，理论上方程组的解不唯一，这为机器人工作轨迹规划带来较多的选择，但求解算法较为复杂。自由度大于6的机器人也称为冗余自由度机器人。

当机器人自由度小于6，即独立的关节变量小于6时，自变量的个数小于独立方程的个数，因而只有对姿态或位置变量做出一些约束，方程组才可能有解。自由度小于6的机器人也称为欠自由度机器人。对于欠自由度机器人，它在工作空间范围内不能达到全部位姿。

当机器人自由度为6，独立的关节变量为6时，自变量的个数等于独立方程的个数，而理论上方程组一般有唯一解。因而一般的通用工业机器人有6个自由度。

对于机器人连杆上两个关节轴线处于空间一般位置（不平行也不垂直）的6自由度串联机器人，其逆向运动学问题至今也没有通用且有效的求解方法。为了简化D-H矩阵，通用工业机器人每个连杆上的两个关节轴线一般不是取为平行就是垂直，这使得运动学方程得到简化，从而降低了逆向运动学问题的求解难度。

在给定机器人末端执行器位姿的前提下，逆向运动学问题可能无解，如位置向量超出机器人的工作空间范围就会出现无解情况。如果逆向运动学问题有解，该解包括封闭解和数值解两种。

封闭解即解析解，即机器人的每个关节变量由包含机器人末端位置和姿态参数的分式、三角函数、指数、对数和无穷级数等基本初等函数所表达的解，它包含了逆向运动学问题的所有解。获得封闭解是研究机器人逆向运动学问题所追求的最理想目标。然而，在有些情况下虽难以获得机器人逆向运动学问题的封闭解，但可以在满足一定精度要求的条件下，利用数值积分、数值微分、插值等数值计算方法求得近似解，这就是数值解。

目前机器人运动学研究的一个重要结论是：所有包含移动关节或转动关节的6自由度串联机器人的逆向运动学问题有解，一般情况下为数值解。对于6自由度串联机器人，其运动副的配置处于特殊情况下，其逆向运动学问题才有封闭解。当6自由度串联机器人满足下列条件之一时，逆向运动学问题有封闭解：

（1）三个相邻关节轴线相交于一点。

（2）三个相邻关节轴线相互平行。

PUMA机器人满足条件（1），因而有封闭解；KUKA机器人和ABB机器人满足条件（2），因而也有封闭解。上述条件（1）和（2）只是逆向运动学有封闭解的充分条件，不满足条件（1）和（2）的机器人也可能有封闭解。设计串联工业机器人时，一般要求逆向运动学问题有封闭解。

对于并联机器人，由于其机构与串联机器人不同，其运动学问题与串联机器人也不同。对于串联机器人，其正向运动学问题求解简单，但逆向运动学问题求解困难；而并联机器人则相反，其逆向运动学问题求解容易，但正向运动学问题求解困难。