对于每一种商用工业机器人，其世界坐标系、工作台坐标系和工件坐标系都可以通过示教的方法进行设定，一般可以采用三点法（或四点法）进行设定。所谓三点法，如图3-16所示，用示教的方法可以确定不在同一直线上的第一点x 1、第二点x 2和第三点y 1；第一点x 1与第二点x 2连线组成坐标系的x轴；通过第三点y 1向x轴作的垂直线，为y轴，交点为坐标系原点；利用向量叉积z＝x×y可以确定z轴。图中的工作台坐标系｛S｝和工件坐标系｛G｝都可以用该方法建立。

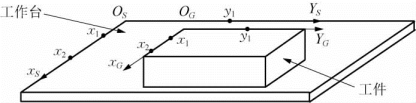
图3-16　三点法设定坐标系原理

机器人现场作业时，需要根据作业任务要求，如焊接作业等，确定目标坐标系（工件坐标系）相对于工作台坐标系的初始位置和姿态以及终了位置和姿态，然后为目标坐标系（工件坐标系）在初始位置和终了位置之间规划出合理的轨迹。因为工具坐标系描述的是末端执行器相对于机器人基坐标系的位置和姿态，因此需要把上述在工作台坐标系规划的轨迹坐标和姿态变换到机器人基坐标系中，其相应的坐标变换为

式中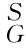，T为目标（工件）坐标系｛G｝相对于工作台坐标系｛S｝的位置和姿态；T为工作台坐标系｛S｝相对于机器人基坐标系｛B｝的位置和姿态；T为目标（工件）坐标系｛G｝相对于机器人基坐标系｛B｝的位置和姿态。

利用上述变换，可以把目标（工件）坐标系｛G｝相对于工作台坐标系｛S｝的轨迹变换到机器人基坐标系中。由于作业过程中，如焊接或者抓取过程中，工具坐标系｛T｝与目标（工件）坐标系｛G｝不一定重合，需要把表示目标（工件）坐标系｛G｝相对于机器人基坐标系｛B｝的位置和姿态T变换成相应的工具坐标系｛T｝“对应”的相对于机器人基坐标系｛B｝的位置和姿态T。因为目标（工件）坐标系｛G｝和工具坐标系之间的位姿关系也可以设定，即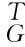T已知。因为T＝TT，故

接下来的问题是如何由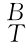T确定机器人的关节变量θ＝［θ1θ2…　θn］T的值。

因为工具坐标系｛T｝相对于法兰坐标系｛F｝的位姿FTT已知，而法兰坐标系｛F｝相对于末端连杆坐标系｛n｝的位姿T也已知，且T＝TT＝TT，故

由此可以求得末端连杆坐标系｛n｝相对应的位姿，把它作为已知量代入机器人运动学方程（3-3）的右端；然后利用方程（3-3）可逐点求出关节角θ＝［θ1θ2…　θn］T。具体求解方法将在第4章逆向运动学讨论。

参考文献

［1］Denavit J，Hartenberg R S．A kinematic notation for lower-pair mechanisms based on matrices［J］．Journal of Applied Mechanics，1955（卷期不详）：215-221．

［2］https：∥en．wikipedia．org／wiki／Denavit%E2%80%93Hartenberg_parameters．

［3］Craig JJ．Introduction to robotics mechanics and control［M］．3rd ed．［S．l．］：Person Education，Inc．Published as Prentice Hall，2005．

［4］Niku S B．Introduction to robotics：analysis，control，applications［M］．2nd ed．［S．l．］：John Wiley ＆ Sons，Inc．，2010．

［5］熊有伦．机器人技术基础［M］．武汉：华中科技大学出版社，2004．

［6］宋伟刚．机器人学：运动学、动力学与控制［M］．北京：科学出版社，2007．

［7］孙树栋．工业机器人技术基础［M］．西安：西北工业大学出版社，2006．(www.daowen.com)

［8］Murray R M，Li Z X，Sastry SS．A mathematical introduction to robotic manipulator［M］．［S．l．］：CRC Press，1994．

［9］小島利夫．ロボツトの制御［M］．［S．l．］：コロナ社，1998．

［10］吉川恒夫．ロボツト制礎諭［M］．［S．l．］：コロナ社，1988．

思考与练习

1.如图3-17所示一3自由度机器人，轴1和轴2垂直。基坐标系｛x 0y 0z0｝如图所示，其中：z0与关节1的旋转轴重合，x 0与x 1轴的初始位置重合。将每个连杆的坐标系建立在上关节，（1）在图中画出连杆1上的坐标系｛x 1y 1z1｝、连杆2上的坐标系｛x 2y 2z2｝和连杆3上的坐标系｛x 3y 3z3｝；（2）写出每个关节的D-H变换参数；（3）试用D-H变换求出T、T、T、T。

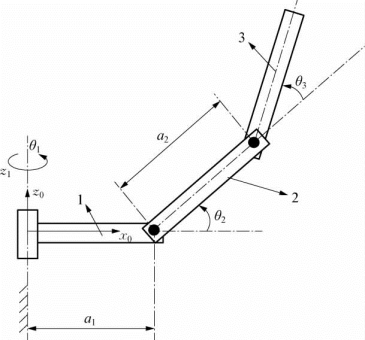
图3-17　平面3R机器人

图3-18　SCARA机器人

2.如图3-18所示SCARA机器人，试确定其D-H参数、每个连杆的D-H矩阵以及末端连杆相对于基座的位姿矩阵T。

3.如图3-19所示的肘关节机器人，试确定其每个连杆的D-H参数、D-H矩阵以及机器人运动学方程。

图3-19　肘关节机器人

图3-20　具有2个移动关节的4自由度机器人

4.试确定如图3-20所示具有2个移动关节和2个转动关节的4自由度机器人的D-H参数，并求其运动学方程。

5.试建立如图3-21所示的三连杆机器人的D-H坐标系，并确定其D-H参数。

图3-21　三连杆机器人

6.试根据机器人连杆D-H参数，应用MATLAB编写求一般串联机器人运动学方程的程序。