当机器人所有连杆的坐标系都按照上述方法确定后,可以采用如下步骤建立机器人的运动学方程。
1)确定D-H参数表
根据所有连杆上建立的坐标系,可以逐一确定其D-H参数,然后填写表3-2。
表3-2 机器人D-H参数表
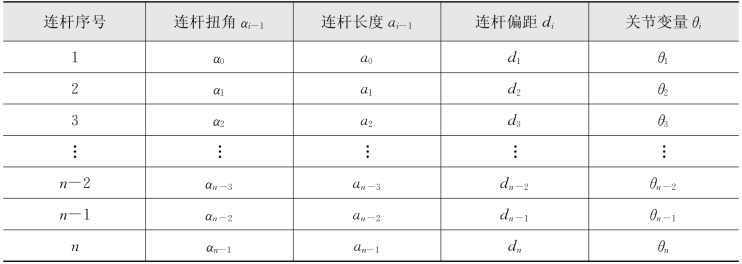
2)计算D-H矩阵
将上述D-H参数分别代入式(3-1),即可以确定n个D-H矩阵: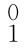 T、
T、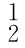 T、…、
T、…、![]()
3)建立机器人运动学方程
根据“位姿矩阵和刚体变换矩阵的关系”的结论,D-H矩阵![]() 的物理意义为:坐标系{i}相对于坐标系{i-1}的位姿,是把坐标系{i}中的向量转换到坐标系{i-1}中的刚体变换;同理,
的物理意义为:坐标系{i}相对于坐标系{i-1}的位姿,是把坐标系{i}中的向量转换到坐标系{i-1}中的刚体变换;同理,![]() 的物理意义为:坐标系{i+1}相对于坐标系{i}的位姿,是把坐标系{i+1}中的向量转换到坐标系{i}中的刚体变换,因此,按照式(2-21),
的物理意义为:坐标系{i+1}相对于坐标系{i}的位姿,是把坐标系{i+1}中的向量转换到坐标系{i}中的刚体变换,因此,按照式(2-21),![]() 为坐标系{i+1}相对于坐标系{i-1}的位姿;同理,
为坐标系{i+1}相对于坐标系{i-1}的位姿;同理,![]() 为坐标系{i+2}相对于坐标系{i-1}的位姿,依此类推,
为坐标系{i+2}相对于坐标系{i-1}的位姿,依此类推,![]() 为坐标系{j}相对于坐标系{i-1}的位姿。因而,自基座开始,按照运动链的关节连接顺序,将D-H矩阵
为坐标系{j}相对于坐标系{i-1}的位姿。因而,自基座开始,按照运动链的关节连接顺序,将D-H矩阵![]() “向右依次拼接”,则可以求得机器人的运动学方程(https://www.daowen.com)
“向右依次拼接”,则可以求得机器人的运动学方程(https://www.daowen.com)
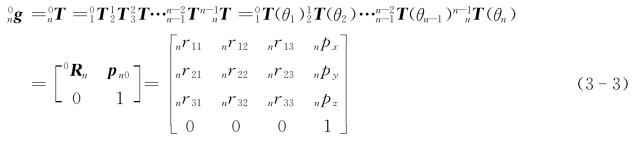
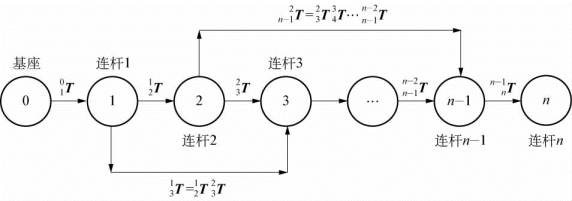
图3-7 机器人运动学方程及坐标变换图
如图3-7所示,连杆3上的坐标系{3}相对于连杆1上的坐标系{1}的位姿矩阵为![]() ;同理,坐标系{j}相对于坐标系{i}的位姿矩阵为
;同理,坐标系{j}相对于坐标系{i}的位姿矩阵为![]() (j>i)。利用机器人连杆D-H参数表,参照式(3-3)可以确定机器人任意连杆i上的坐标系{i}相对于机器人基座坐标系{0}的位姿为
(j>i)。利用机器人连杆D-H参数表,参照式(3-3)可以确定机器人任意连杆i上的坐标系{i}相对于机器人基座坐标系{0}的位姿为
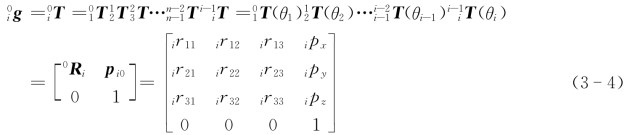
式(3-4)除了可以用于确定连杆i相对于机器人基座的位姿外,在求解连杆i的速度(包括线速度和角速度)以及动能时也要用到。
式(3-3)中的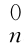 g=
g= T=
T=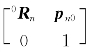 表示机器人运动链上末端连杆n上的坐标系{n}相对于坐标系{0}的位姿,其中0R n表示坐标系{n}相对于坐标系{0}的姿态;向量p n0表示坐标系{n}的原点在坐标系{0}中的位置向量。
表示机器人运动链上末端连杆n上的坐标系{n}相对于坐标系{0}的位姿,其中0R n表示坐标系{n}相对于坐标系{0}的姿态;向量p n0表示坐标系{n}的原点在坐标系{0}中的位置向量。
对于式(3-3)所示的机器人而言,一旦关节变量θ=[θ1θ2… θn]T已知,将其代入式(3-3)可以计算出矩阵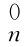 T=
T=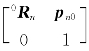 ,它完全确定了在当前时刻,机器人末端连杆n的坐标系{n}的原点在基坐标{0}的位置p n0,以及坐标系{n}相对于基坐标{0}的姿态0R n。
,它完全确定了在当前时刻,机器人末端连杆n的坐标系{n}的原点在基坐标{0}的位置p n0,以及坐标系{n}相对于基坐标{0}的姿态0R n。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






