1955年，Denavit和Hartenberg提出一种基于矩阵变换描述低副运动机构运动的方法，称为D-H矩阵法。这种方法的核心是定义了连杆参数，称为D-H参数；也定义了连杆坐标系，称为D-H坐标系。该方法是研究空间机构运动最常用的方法，因而商用机器人一般都采用该方法描述机器人的运动。

D-H矩阵定义连杆参数的方法如图3-3所示。中间连杆i－1上有两个关节，其上关节轴线为轴i－1，下关节轴线为轴i。连杆i－1一旦制造装配完毕，其上的轴线i－1和轴线i的相对位置不会发生变化（否则连杆i－1不是发生变形，就是因过载而产生破坏）。因而连杆i－1的上关节轴线i－1与下关节轴线i之间最短的距离，即轴线i－1与轴线i的公垂线长度ai－1，不会发生变化；同时，关节轴线i－1与关节轴线i的夹角αi－1也不会发生变化，如图3-3所示。

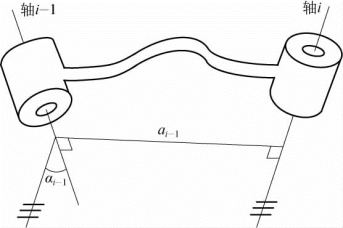
图3-3　连杆参数——长度和扭角

连杆参数规定：

1）连杆i－1长度ai－1

关节轴线i－1与关节轴线i的公垂线长度ai－1，规定为连杆i－1的长度。当关节i和关节i－1的轴线相交时，ai－1＝0。

2）连杆i－1扭角αi－1

关节轴线i－1与关节轴线i的夹角αi－1称为连杆扭角。当关节i和关节i－1的轴线平行时，αi－1＝0。αi－1的正负规定为：按照右手定则，右手的拇指指向轴线xi－1的方向（图3-4）；右手四指伸直指向zi－1的方向，如果四指是沿逆时针（从面向xi－1轴的方向看）转动角度αi－1后与zi重合，则角度αi－1的值为正；否则αi－1的值为负。

基于连杆i－1长度ai－1和连杆i－1扭角αi－1这两个参数，可以研究基于连杆“上关节”的D-H坐标系的建立方法。

对于连杆i－1，如图3-4所示，为了研究连杆i－1的运动，需要在连杆i－1上建立坐标系｛xi－1yi－1zi－1｝。一种方法是把坐标系建立在连杆i－1的“上关节”，这种方法也称为修正D-H参数方法或改进D-H参数方法。取zi－1与关节轴线i－1重合，并取定正方向，如图3-4所示；取xi－1与公垂线ai－1重合，方向指向下关节轴线i。根据右手定则，yi－1可由zi－1和xi－1的叉积确定：yi－1＝zi－1×xi－1。

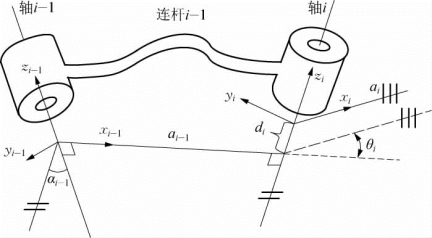
图3-4　连杆坐标系

同理，对于连杆i上的坐标系｛xiyizi｝，也可以用上述方法确定，如图3-4所示。

3）关节变量θi

由图3-4可以看出，连杆i－1上的坐标系｛xi－1yi－1zi－1｝的坐标轴xi－1与连杆i上的坐标系｛xiyizi｝的坐标轴zi垂直（ai－1是公垂线）；同时，连杆i上的坐标系｛xiyizi｝的坐标轴xi与｛xiyizi｝的坐标轴zi垂直，设xi与x i－1的夹角为θi，θi称为关节变量或关节角。θi的正负规定为：按照右手定则，右手的拇指指向轴线zi的方向；右手四指伸直指向xi－1的方向，如果四指是沿逆时针（从面向zi轴的方向看）转动角度θi后与x i重合，则角度θi的值为正；否则θi的值为负。连杆i相对于连杆i－1的旋转角度相对于关节轴线i测量，如关节是转动关节，则它是关节变量θi。(www.daowen.com)

如图3-4所示，θi的变化可以反映连杆i相对于连杆i－1的运动，即连杆i相对于连杆i－1轴线i的转动，因此θi为描述连杆i与连杆i－1之间相对运动的参数。

4）连杆偏距di

由图3-4可以看出，连杆i－1上的坐标系｛xi－1yi－1zi－1｝的坐标轴xi－1与连杆i上的｛xiyizi｝的坐标轴xi沿z i轴的距离为d i，di称为连杆偏距。di的正负规定为：轴xi－1与轴zi的交点（垂足）到轴xi与轴z i轴的交点（垂足）的方向与zi轴正方向一致时，di取为正；否则di取负值。di沿关节轴线i测量，如关节是移动关节，则它是关节变量。

综上所述，连杆i－1长度ai－1、连杆i－1扭角αi－1、关节角θi以及连杆偏距di完全确定了坐标系｛xi－1yi－1zi－1｝与坐标系｛xiyizi｝的相对位置关系，这四个参数称为连杆参数。

根据第2章2.2.5节中的“位姿矩阵和刚体变换矩阵的关系”的结论，要确定坐标系｛xiyizi｝相对于坐标系｛xi－1yi－1zi－1｝的位置和姿态，只要能对坐标系｛xi－1yi－1zi－1｝“施加”一系列刚体运动，使得坐标系｛xi－1yi－1zi－1｝与坐标系｛xiyizi｝重合，则与该过程相对应的刚体变换矩阵即为｛xiyizi｝相对于坐标系｛xi－1yi－1zi－1｝的位姿矩阵。如图3-5所示，要使得坐标系｛xi－1yi－1zi－1｝与坐标系｛xiyizi｝的重合，可以通过以下四个基本运动实现：

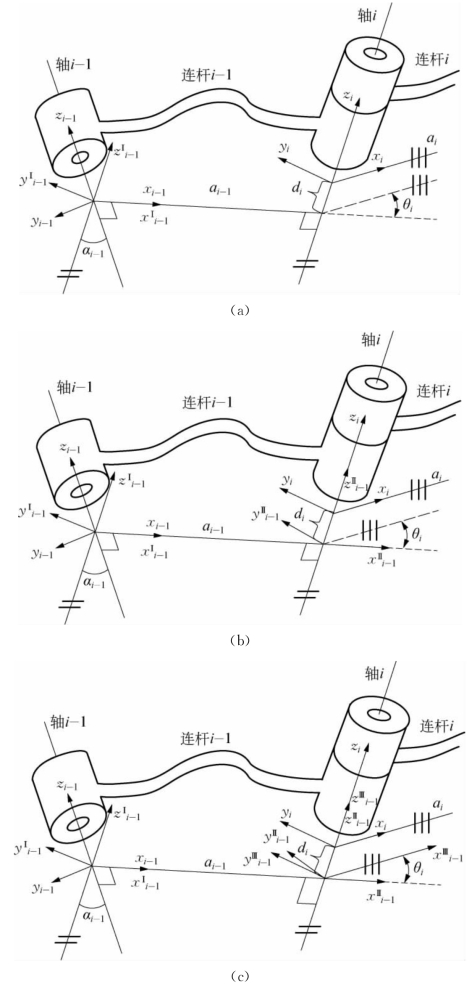
图3-5　使坐标系｛xi－1yi－1zi－1｝与坐标系｛xiyizi｝重合的刚体运动

（1）让坐标系｛xi－1yi－1zi－1｝绕自身轴线xi－1旋转角度αi－1，使得轴线zi－1与轴线zi平行且同向，达到位置，如图3-5a所示；与之对应的刚体变换矩阵为Rot（x，αi－1）。

（2）让坐标系沿自身轴线平移距离ai－1，使得轴线与轴线zi重合，达到位置，如图3-5b所示；与之对应的刚体变换矩阵为Tra（x，ai－1）。

（3）让坐标系绕自身轴线旋转角度θi，使得轴线与轴线xi平行且同向，达到位置，如图3-5c所示；与之对应的刚体变换矩阵为Rot（z，θi）。

（4）让坐标系沿自身轴线平移距离di，使得坐标系与坐标系｛xiyizi｝完全重合，如图3-5c所示；与之对应的刚体变换矩阵为Tra（z，di）。

根据“位姿矩阵和刚体变换矩阵的关系”的结论，与上述四个全过程相对应的总的刚体变换矩阵T，即为｛xiyizi｝相对于坐标系｛xi－1yi－1zi－1｝的位姿矩阵。上述四个基本运动都是绕当前坐标系的坐标轴旋转或平移，因而，用相对于当前坐标系坐标轴的旋转矩阵或平移矩阵描述刚体运动最为简便。因而，可以按照第2章2.2.7节变换矩阵“右乘法则”得到，即

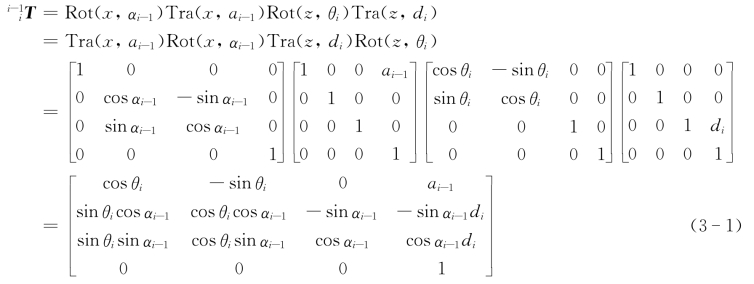
为了简化机构和便于控制，一般工业机器人同一连杆上的两个运动副的轴线均取为平行或垂直，故式（3-1）所示的D-H矩阵可以得到简化，从而便于机器人连杆的设计制造以及机器人的运动控制。

应该指出，由于坐标系z轴方向选取的不同、坐标系原点（当连杆上两个关节轴线平行时）的选择不同，连杆的D-H参数的值不唯一，因而D-H矩阵也不唯一。