如图2-18所示，刚体由初始位姿为g0，绕过Q点的轴线k旋转角度θ，再沿轴线k平移距离h后的位姿为g t。上述刚体运动既可以在坐标系｛A｝中描述，也可以在坐标系｛B｝中描述。

当刚体运动在坐标系｛A｝中描述时，Q点和轴线k在坐标系｛A｝中表示为QA和k A，即Q A＝［qxAqyAqzA］T；k A＝［kxAkyAkzA］T，其中kxA、kyA、kzA为向量k在坐标系｛A｝的x A轴、y A轴和z A轴上的投影。其相应的刚体变换为T［Rot（QA，k A，θ），Tra（h k A）］。由式（2-43）可知

Ag t＝T［Rot（QA，k A，θ），Tra（h k A）］Ag 0

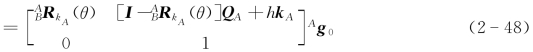
刚体变换T［Rot（QA，k A，θ），Tra（h k A）］“左乘”刚体初始位姿矩阵Ag 0得到刚体运动后的位姿矩阵Ag t。

上述刚体运动也可以在坐标系｛B｝中描述。设Q点和轴线k在坐标系｛B｝中表示为QB和k B，即Q B＝［qxBqyBqzB］T；k B＝［kxBkyBkzB］T，其中kxB、kyB、kzB为向量k在坐标系｛B｝的x B轴、y B轴和z B轴上的投影。在上述刚体运动在坐标系｛B｝中描述的刚体变换为T［Rot（QB，k B，θ），Tra（h k B）］。从“运动效果”上看，刚体在坐标系｛B｝中，从初始位姿Ag 0绕轴线k B旋转角度θ，再沿k B轴移动距离h，同样达到了相同的“位置”，即位姿Ag t。参照式（2-44），绕轴k B转动θ角，再沿轴k B平移h的刚体变换为

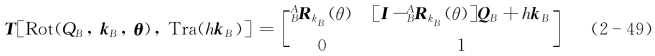
其中

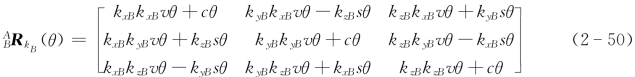
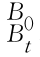由刚体变换矩阵T蕴含的物理意义可知，刚体运动在坐标系｛B｝中的描述，即刚体变换矩阵BT，为刚体运动后坐标系｛B｝在当期位置｛Bt｝相对于其初始位置｛B 0｝的位姿B0Btg。因而，当刚体绕轴线k B旋转角度θ，再沿轴线k B平移距离h后，坐标系｛Bt｝相对于坐标系｛B0｝的位姿0 g为g＝T［Rot（QB，k B，θ），Tra（h k B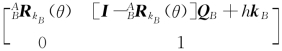）］＝；而坐标系｛B0｝相对于坐标系｛A｝的位姿为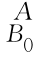g0＝Ag 0，根据式（2-21），坐标系｛Bt｝相对于坐标系｛A｝的位姿Ag t为

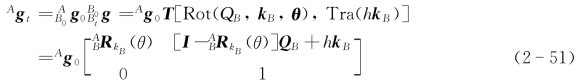
式（2-51）表明，坐标系｛B｝中描述的刚体变换矩阵T［Rot（QB，k B，θ）］“右乘”刚体的初始位姿Ag 0得到刚体运动后相对于坐标系｛A｝的位姿Ag t。

由式（2-48）和式（2-51）可得

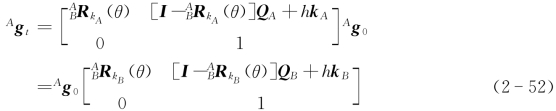
由式（2-52）可知，坐标系｛A｝中描述的刚体变换T［Rot（QA，k A，θ），Tra（h k A）］和坐标系｛B｝中描述的刚体变换T［Rot（QB，k B，θ），Tra（h k B）］之间的关系为

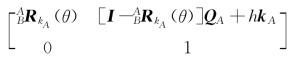
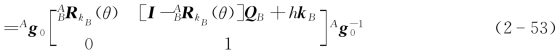
其中向量k和点Q在坐标系｛A｝中的坐标k A、QA与它们在坐标系｛B｝中的坐标k B、QB之间的关系可以由式（2-17）和式（2-19）确定

式（2-53）表明：对于同一个刚体运动，坐标系｛A｝中描述的刚体变换矩阵与坐标系｛B｝中描述的刚体变换矩阵是“相似”矩阵。

式（2-53）的物理解释为：如图2-20所示，坐标系｛B｝和坐标系｛A｝“同时”由各自初始位置｛B0｝、｛A0｝绕k轴旋转θ、再沿着k平移距离h后，分别处于位置｛Bt｝和｛At｝；因为坐标系｛B｝和坐标系｛A｝“一起”或“同步”运动，故坐标系｛Bt｝相对于坐标系｛At｝位姿仍为g0；而在运动末了时刻，坐标系｛Bt｝相对于其初始位置｛B0｝的位姿为T［Rot（QB，k B，θ），Tra（h k B）］，而坐标系｛B 0｝相对于坐标系｛A 0｝的位姿为g0；故根据式（2-21），｛Bt｝相对于坐标系｛A 0｝的位姿Ag t为

Ag t＝Ag 0T［Rot（QB，k B，θ），Tra（h k B）］

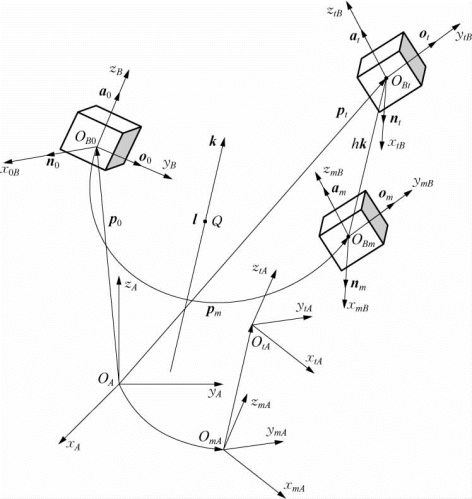
图2-20　在不同坐标系中描述的“同一刚体运动”的两个刚体变换的关系

另外，在运动末了时刻，坐标系｛Bt｝相对于坐标系｛At｝位姿仍为Ag 0；而此时，坐标系｛At｝相对于其初始位置｛A 0｝的位姿为T［Rot（QA，k A，θ），Tra（h k A）］，故根据式（2-21）可得｛Bt｝相对于坐标系｛A 0｝位姿Ag t为

Ag t＝T［Rot（QA，k A，θ），Tra（h k A）］Ag 0

由上两式可得

Ag t＝Ag 0T［Rot（QB，k B，θ），Tra（h k B）］＝T［Rot（QA，k A，θ），Tra（h k A）］Ag 0

由线性代数可知，对于矩阵M、N，若存在可逆矩阵P，满足M＝PNP－1或P－1MP＝N，则称矩阵M与矩阵N相似。因而，对于同一刚体运动，坐标系｛A｝描述的刚体变换矩阵T［Rot（QA，k A，θ），Tra（h k A）］与坐标系｛B｝描述的刚体变换矩阵T［Rot（QB，k B，θ），Tra（h k B）］矩阵是相似矩阵。反之，如果两个刚体变换矩阵AT和BT相似，则它们描述的是同一个刚体运动，区别是在两个不同的坐标系｛A｝和｛B｝中描述该运动。

在刚体上建立与其“固定连接”的坐标系｛B｝，坐标系｛B｝相对于坐标系｛A｝的初始位姿为Ag 0，对于同一个刚体运动，既可以在坐标系｛A｝中描述为矩阵AT，也可以在坐标系｛B｝中描述为矩阵BT，它们的作用如下：

（1）刚体运动后的位姿g t等于坐标系｛A｝中描述的刚体变换矩阵AT“左乘”初始位姿g0，即g t＝ATg 0；g t也等于坐标系｛B｝中描述的刚体变换矩阵BT“右乘”初始位姿g0，即g t＝g0BT。

（2）变换矩阵AT和变换矩阵BT是相似矩阵。反之，若两个刚体变换相似，则它们描述的是同一个刚体运动。通过相似变换，有助于简化刚体运动分析。

（3）刚体运动是选择在坐标系｛A｝中描述还是选择在坐标系｛B｝中描述，取决于哪一种变换矩阵的计算更简便。

刚体变换矩阵左乘和右乘刚体的当前位姿矩阵，它们对应的刚体运动分别是在“惯性坐标系”｛A｝描述以及在当前坐标系｛B｝描述。由于刚体变换矩阵在当前坐标系｛B｝中描述有时更为简洁，因而可以利用“右乘”简化计算过程，这为导出描述机器人连杆运动的D-H变换矩阵奠定了基础。

（4）绕同一个轴连续进行的两个刚体变换，其变换矩阵乘积可以交换。

例如，刚体绕同一轴线k先旋转角度θ，再平移距离d，其运动结果与刚体先沿轴线k平移距离d，在绕轴线k旋转角度θ完全相同。因而，相对应的两个变换矩阵可以交换。

【例2-1】　如图2-21所示，刚体相对于坐标系｛A｝的初始位姿为

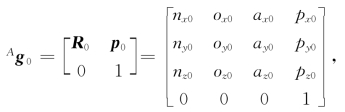
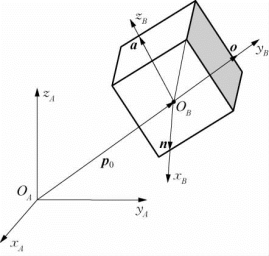
图2-21　刚体初始位姿

试求刚体绕坐标系｛B｝的轴x B旋转θ角后，相对于坐标系｛A｝的位姿Ag t。

解法1：利用“左乘”——刚体变换在坐标系｛A｝中描述。(www.daowen.com)

根据位姿矩阵的含义，坐标系｛B｝的x B轴正方向的单位向量在坐标系｛A｝中的坐标为（nx0，ny0，nz0）T，取k A＝（nx0，ny0，nz0）T。在坐标系｛A｝中，沿过点OB＝p0＝［p x0p y0pz0］T的轴线k A旋转角度θ的刚体运动，其对应的刚体变换R kA（θ）为可由式（2-38）确定，即

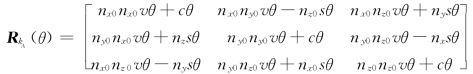
利用式（2-43）或式（2-48）可得

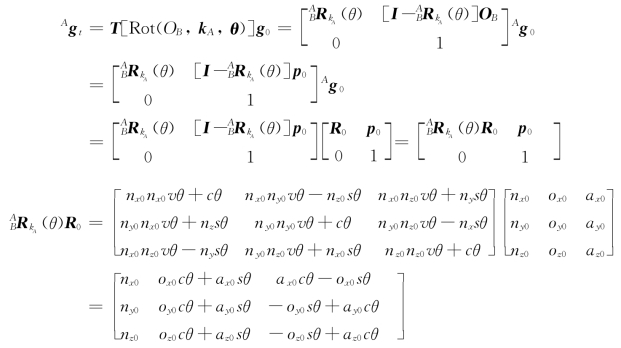
则根据式（2-51），经过上述运动后，刚体B相对于坐标系｛A｝的位形为

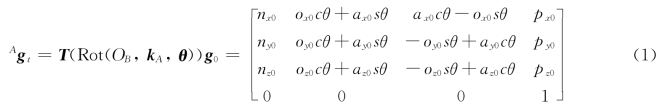
解法2：利用“右乘”——刚体变换在坐标系｛B｝中描述。

若从坐标系｛B｝上看，绕x B轴旋转相对应的刚体变换为

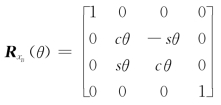
根据式（2-51），利用刚体变换矩阵RxB（θ）右乘同样可获得刚体运动后相对于坐标系｛A｝的位形为

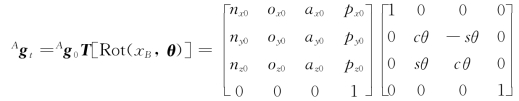
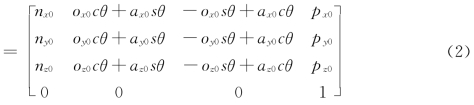
由式（1）和式（2）右边矩阵的结果可得

T［Rot（OB，k A，θ）］Ag 0＝Ag 0T［Rot（x B，θ）］

虽然两种方法的运算结果一样，但是，上述刚体变换在坐标系｛B｝中描述显然更为简便。

参考文献

［1］Craig J J．Introduction to robotics mechanics and control［M］．3rd ed．［S．l．］：Person Education，Inc．Published as Prentice Hall，2005．

［2］Niku S B．Introduction to robotics：analysis，control，applications［M］．2nd ed．［S．l．］：John Wiley ＆ Sons，Inc．，2010．

［3］Murray R M，Li Z X，Sastry S S．A mathematical introduction to robotic manipulator［M］．［S．l．］：CRC Press，1994．

［4］肖尚彬．元数方法及其应用［J］．力学进展，1993，23（2）：249-260．

［5］熊有伦．机器人技术基础［M］．武汉：华中科技大学出版社，2004．

［6］宋伟刚．机器人学：运动学、动力学与控制［M］．北京：科学出版社，2007．

［7］孙树栋．工业机器人技术基础［M］．西安：西北工业大学出版社，2006．

［8］https：∥en．wikipedia．org／wiki／Conversion_between_quaternions_and_Euler_angles．

思考与练习

1.如图2-22所示，向量v0分别绕坐标系x轴、y轴和z轴旋转α、β、γ角度后，其坐标v t分别是多少？

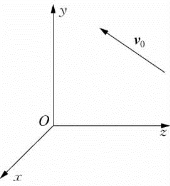
图2-22　向量的旋转

2.试证明：式（2-38）所示的刚体绕任意轴k旋转的刚体变换矩阵。

3.在图2-18所示的刚体运动中，试证明坐标系｛A｝的原点随刚体运动后的坐标为p＝［I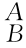－R kA（θ）］Q A。

4.试证明：相对于

同一个轴k连续

进行的两个刚体运动（转动或移动），其对应的刚体变换矩阵可以交换。证明过程可以分为以下几种情况讨论：

（1）沿轴线k平移距离l 1，对应的刚体变换矩阵为T（k，l1）；沿轴线k平移距离l 2，对应的刚体变换矩阵为T（k，l 2），证明：T（k，l1）T（k，l2）＝T（k，l 2）T（k，l1）。

（2）沿轴线k旋转角度θ1，对应的刚体变换矩阵为R（k，θ1）；沿轴线k旋转角度θ2，对应的刚体变换矩阵为R（k，θ2），证明：R（k，θ1）R（k，θ2）＝R（k，θ2）R（k，θ1）。

（3）沿轴线k平移距离l 1，对应的刚体变换矩阵为T（k，l 1）；沿轴线k旋转角度θ2，对应的刚体变换矩阵为R（k，θ2），证明：T（k，l1）R（k，θ2）＝R（k，θ2）T（k，l1）。

5.如图2-8所示，在刚体B上建立与其固定连接的坐标系｛x By Bz B｝；设刚体B相对于坐标系｛x Ay Az A｝的初始位姿为Ag 0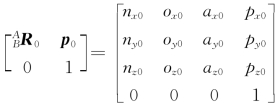＝。试求：

（1）刚体B绕自身轴线x B、y B和z B分别旋转30°、60°和45°后，刚体B相对于坐标系｛A｝的位姿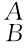g t分别是什么？

（2）刚体B绕轴线x A、y A和z A分别旋转30°、60°和45°后，刚体B相对于坐标系｛A｝的位姿Ag t是什么？

（3）刚体B绕自身轴线x B旋转30°之后，再绕坐标系｛A｝的z A轴旋转60°，刚体B相对于坐标系｛A｝的位姿Ag t是什么？

（4）刚体B绕坐标系｛A｝的z A轴旋转60°，再绕自身轴线x B旋转30°之后，刚体B相对于坐标系｛A｝的位姿Ag t是什么？

6.试用MATLAB编制求式（2-20）所示的刚体位姿矩阵的逆矩阵程序。