刚体的位移，即刚体在空间的运动状态发生变化，是通过刚体的初始位姿g0和末了位姿g t的变化来描述的，为此，需要确定初始位姿g0和末了位姿g t之间的关系T，称为刚体变换，其表达式为

g t＝Tg 0　（2-23）

其中

因为位姿矩阵可逆，故式（2-23）的两端右乘g0的逆矩阵g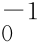可得

只要证明矩阵R是旋转矩阵，就证明了刚体变换矩阵与位姿矩阵具有相同的结构。

事实上，只要注意到姿态矩阵R t和R 0是旋转矩阵（正交矩阵），即R t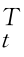R＝R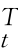R t＝I，R0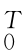R＝R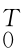R0＝I，从而可以得到

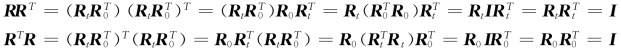
上两式表明，两个旋转矩阵相乘，其结果仍为旋转矩阵，因而式（2-24）中的矩阵R是旋转矩阵。

描述刚体位姿和刚体变换目前常用的方法包括位姿矩阵法、旋量法和四元素法等。这些方法各有优缺点，本书采用位姿矩阵法。目前的商用工业机器人，如ABB等主要采用位姿矩阵法，而KUKA机器人则采用旋量法。

为了便于深入研究刚体运动，特别是多个刚体运动的“叠加”结果，需要理解刚体变换矩阵的物理意义，这就是沙勒（Chasles）定理。

（1）刚体一般运动（转动和平动的组合）的沙勒定理。由理论力学中的沙勒定理可知，刚体的位移可以通过绕某一轴线的“转动”加上绕该轴线的“平移”来实现。刚体变换T和式（2-18）表示的位姿矩阵虽然具有相同的形式，但其物理意义不同。事实上，如图2-10所示，刚体从初始位姿g0到位姿g t的位移，根据沙勒定理，都可以通过让该刚体绕某一轴（向量）k旋转角度θ，加上沿该轴（向量）k的平移一段距离d的“组合”运动来实现。式（2-24）中的旋转矩阵R就代表刚体绕轴（向量）k的旋转运动；但列向量p并不是刚体绕该轴（向量）k的平移运动，它是坐标系｛A｝的原点随刚体运动后的位置向量。

图2-10　刚体变换矩阵的物理意义

事实上，旋转矩阵T可以做如下分解：

式中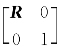，代表刚体绕轴线k的转动；代表沿轴线k的平移运动d＝RTp。

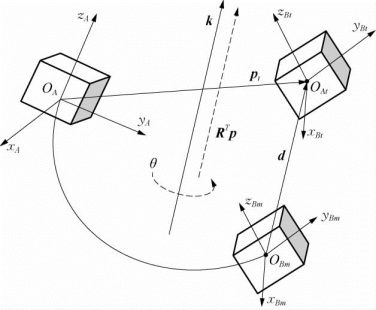
图2-11　刚体位姿矩阵和刚体变换的关系

（2）位姿矩阵和刚体变换矩阵的关系。当取g0＝I（四阶单位阵）时，g t＝Tg 0＝TI＝T，此时位的位姿矩阵g t等于刚体变换矩阵T，即坐标系｛B｝相对于坐标系｛A｝的位姿g t，也就是把坐标系｛A｝由初始位置变换到与坐标系｛B｝的当前位置“重合”时对应的刚体变换T，它是通过绕某一轴线k旋转一定角度θ，到达位置（xmy mz m），再沿该轴线平移距离d来实现的，如图2-11所示。这为求坐标系之间的位姿矩阵提供了一种方法，该方法将在第3章确定D-H矩阵和建立机器人运动学方程中得到应用。

（3）向量经过刚体运动后，仅仅与转动运动有关，而与刚体的平移运动无关。

设刚体运动前的向量为v0，经过刚体运动后变为v t，由式（2-16）可知

即v t＝Rv 0，因此上述结论成立。

（4）刚体变换矩阵T＝中向量p的物理意义：坐标系｛A｝的原点OA0的齐次坐标为［0　1］T，随上述刚体运动后，该原点位置变为O At，且，即O At＝p，因此，向量p即为坐标系｛A｝的原点OA0随刚体运动后的位置向量O At。

刚体在空间中运动分为平动、绕定轴的转动以及一般运动（既有平动，又有转动），下面将分别分析与这三种类型的运动相对应的刚体变换T。

1）刚体平动

如图2-12所示，刚体的平动，是指在运动过程中刚体的姿态一直保持不变，即任意时刻t刚体的姿态矩阵R t与初时刻t＝0时的位姿矩阵R0关系为R t≡R0。因而刚体做平动时，刚体上所有点的运动轨迹相同，该轨迹可能是直线，也可能是曲线。

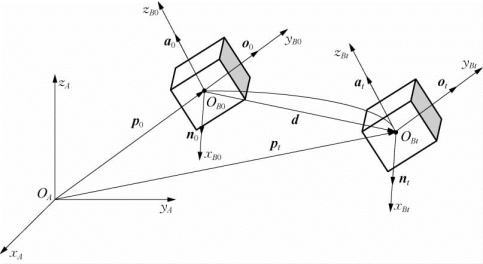
图2-12　刚体平动

设刚体运动的初始位置向量为p 0，任意时刻t的位置向量为p t，则刚体在t＝0和t时刻的位姿矩阵g 0和g t分别为

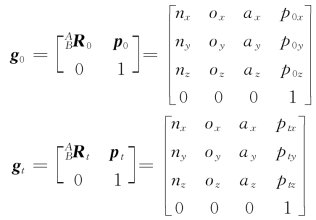
因为刚体做平动，刚体上所有点的位移相同，均等于坐标系｛B｝原点的位移，即

d＝p t－p 0＝［dxd ydz］T＝［ptx－p 0xpty－p 0yptz－p 0z］T　（2-27）

为求刚体由位姿g 0到位姿g t的刚体变换Tra（d，l），令

g t＝Tra（d，l）g0　（2-28）

由式（2-20）可知位姿矩阵g0可逆，故式（2-28）两端右乘g可得

Tra（d，l）＝g tg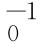　（2-29）

对于刚体做平动，对应的刚体变换为

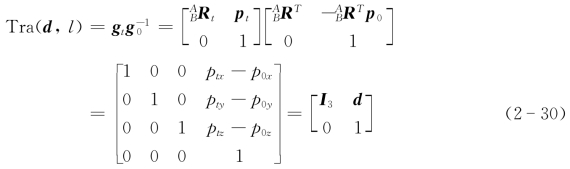
由式（2-30）可知，刚体平移时，其位移只取决于“首末”位置，该运动“等效于”刚体沿着向量d平移了距离l＝‖d‖。

2）刚体转动

刚体转动可分为刚体绕坐标轴旋转、刚体绕通过坐标原点的一般轴线的旋转，以及刚体绕空间任意轴的旋转三种情况。

（1）刚体绕坐标轴旋转的刚体变换。以绕x轴转动为例，如图2-13a所示，坐标系｛B｝和坐标系｛A｝在初始时刻t＝0时重合。

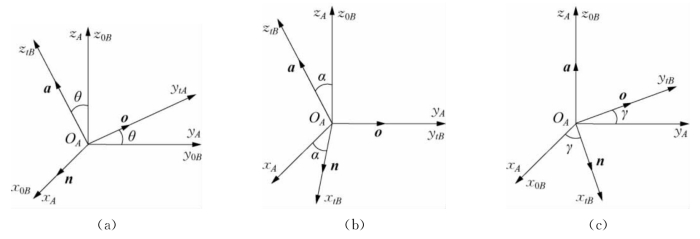
图2-13　绕坐标轴旋转

如图2-13a所示，当坐标系｛B｝绕x A轴逆时针旋转角度θ后，x 0B轴与x 0A轴仍然重合，因此∠n x A＝0，∠n y A＝π／2，∠n z A＝π／2，∠o x A＝π／2，∠o y A＝θ，∠o z A＝π／2－θ，∠a x A＝π／2，∠a y A＝π／2＋θ，∠a z A＝θ，将这些参数代入式（2-4）可得姿态矩阵（旋转矩阵）为

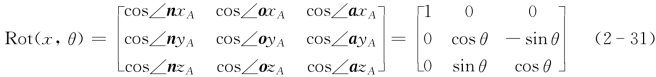
同理，如图2-13b所示，刚体绕y A轴转动α角度后的位姿矩阵（旋转矩阵）为

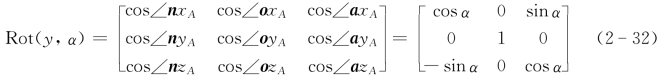
同理，绕z A轴转动γ角度后的位姿矩阵（旋转矩阵）为

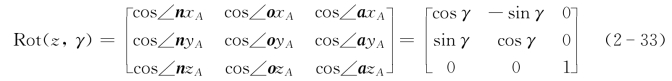
分析式（2-31）～式（2-33）可以发现，绕坐标轴旋转矩阵的特点可以用图2-14描述。

图2-14　绕坐标轴旋转的变换矩阵特点示意图

①如图2-14所示，绕某一轴旋转角度φ，设与该轴对应的数字为i（i＝1，2，3），则旋转矩阵的第“i”行“i”列对应的元素为1，其余两个主对角元素均为转角φ的余弦值。

以绕y轴旋转为例，图中与y轴对应的数字为“2”，则旋转矩阵的第“2”行第“2”列元素为“1”，另外两个主对角元素为cosφ。

②元素1所在的行和列的其余元素为0；矩阵的其余的副对角元素为转角φ的正弦值。

③“负号”的位置，由旋转轴以外的另外两个数字按逆时针顺序决定，如绕x轴旋转，则“1”以外的另外两个数字为“2”和“3”，则“负号”出现在“2→3”，即第2行第3列；同理，绕z轴旋转，则“负号”出现在“1→2”，即第1行第2列。

如图2-15所示，刚体处于空间一般位置，初始位姿为g0，该刚体绕坐标系｛A｝的x轴转动θ后的位姿为g t，由位姿g0→g t相对应的刚体变换为T［Rot（x，θ）］，则有(www.daowen.com)

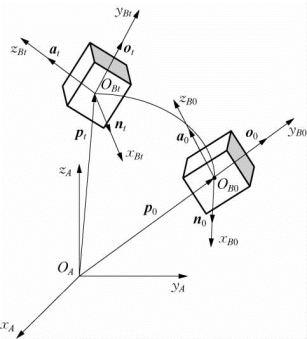
图2-15　绕x轴旋转的刚体变换

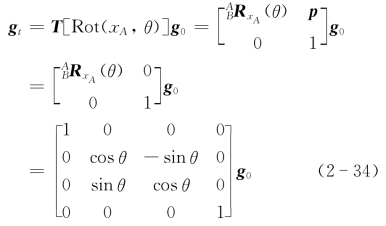
式中，p为坐标系｛A｝的原点由初始位置［0　0　0］T随刚体运动后的位置。因为原点O在x A轴上，故该原点绕x A轴旋转后位置不变，因而p＝［0 0　0］T。

同理，绕坐标系｛A｝的y轴旋转α角度对应的刚体变换T［rot（y，α）］为

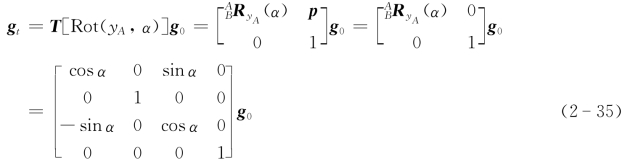
式中，因为坐标系｛A｝的原点绕y A轴旋转后不变，故p＝［0　0　0］T。

绕坐标系｛A｝的z轴旋转γ角度对应的刚体变换T［Rot（z，γ）］为

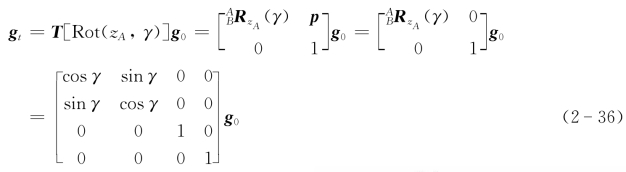
图2-16　绕过坐标系｛A｝的原点　　的k轴旋转变换

式中，因为坐标系｛A｝的原点绕z A轴旋转后不变，故p＝［0　0　0］T。

（2）绕过坐标系原点的一般轴线旋转的刚体变换。如图2-16所示，刚体处于空间一般位置，刚体运动为绕过坐标系｛A｝原点的直线l做旋转运动，旋转角度为θ；设k A为直线l的单位向量，k A＝［k Axk Ayk Az］T，且‖k A‖＝＝1。该刚体的初始位姿为g0，旋转后的位姿为g t，由位姿g0→g t相对应的刚体变换为T［Rot（k A，θ）］为

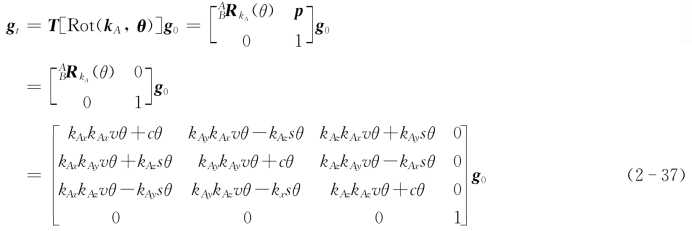
其中

cθ＝cosθ，sθ＝sinθ，vθ＝1－cosθ

式中，p为坐标系｛A｝的原点由初始位置［0　0　0］T随刚体运动后的位置向量；因为原点O在k A轴上，故原点绕k A轴旋转后位置不变，因而p＝［0　0　0］T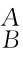；R kA（θ）称为绕过原点的k A轴的旋转矩阵，其表达式为

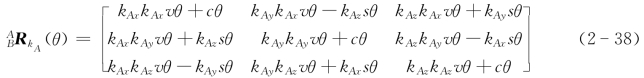
当分别取k A＝［1　0　0］、k A＝［0　1　0］、k A＝［0　0　1］时，式（2-38）分别与式（2-31）～式（2-33）一致，即绕坐标系｛A｝的x轴、y轴和z轴转动，是绕过原点的k轴的旋转矩阵的特例。

当旋转矩阵或姿态矩阵R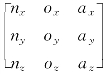＝已知时，如何确定与相对应的旋转轴k和旋转角度θ？

可令

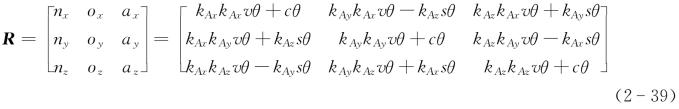
由nx＝k Axk Axvθ＋cθ，oy＝k Ayk Ayvθ＋cθ，az＝k Azk Azvθ＋cθ可得

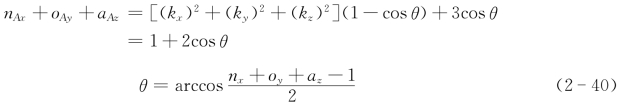
同理，可得

（3）绕空间一般轴线旋转的刚体变换。如图2-17所示，刚体处于空间一般位置，刚体运动为绕过坐标系Q点的直线l（不一定过原点）做旋转运动，旋转角度为θ；k A为直线l的单位向量，设k A＝［k Axk Ayk Az］T，且‖k A‖＝＝1。设该刚体的初始位姿为g0，旋转后的位姿为g t。

由式（2-38）可得，刚体绕k A轴旋转的变换矩阵为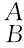R kA（θ），故刚体由位姿g0→g t相对应的刚体变换为T［Rot（QA，k A，θ）］为

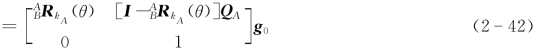
式中，p＝［I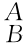－RkA（θ）］QA为坐标系｛A｝的原点O随刚体运动后的坐标，其中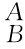RkA（θ）的表达式同式（2-38）。

图2-17　空间一般轴线k的旋转变换

3）刚体的一般运动变换

刚体的一般运动是指刚体运动中包含有平动和转动。由理论力学中的沙勒定理可知，任意刚体运动都可以通过绕某一轴线的平移运动加上绕该轴线的转动来实现。

如图2-18所示，若已知初始位姿为g0，运动后的位姿为gt。根据沙勒定理，位姿g0→gt之间的刚体运动可以通过绕某一点QA的轴线l旋转角度θ，再沿轴线l平移距离h来实现。与该运动相对应的刚体变换为T［Rot（QA，kA，θ），Tra（hkA）］。可以分两步求出该变换。

第一步：求刚体绕点Q的轴线l旋转角度θ后的位姿为gm，即g0→gm。由式（2-42）可得

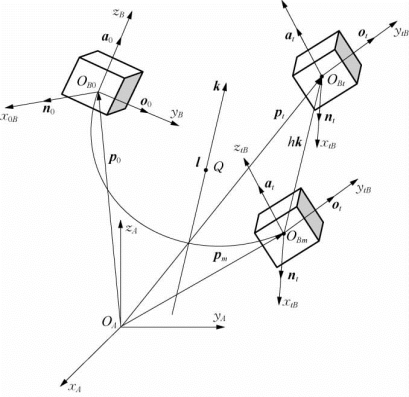
图2-18　刚体的一般运动

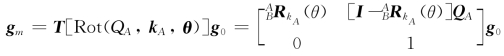
第二步：求刚体由位置xmy mz m经过平移后的位姿g t，即g m→g t。

由式（2-30）可得平移h k A对应的刚体变换为

故由上两式可得

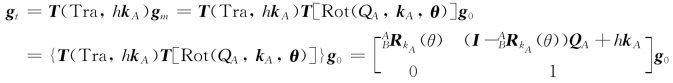
即

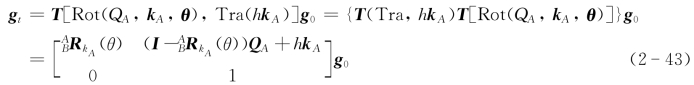
其中

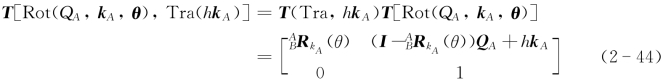
式（2-44）成立的原因是：绕同一个轴连续进行的两个刚体运动，其对应的刚体变换矩阵可以交换。

由式（2-43）可得

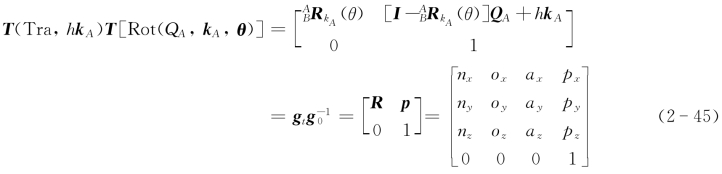
若已知刚体变换矩阵T＝，如何确定其旋转轴k A、旋转角度θ、平移距离d以及轴线k A的位置？

可以利用式（2-40）和式（2-41）求出刚体旋转角度θ和旋转轴线的单位向量k A。下面将确定直线上的点QA（不唯一）和平移距离h。

由于刚体B上所有的点在k A方向的位移相同，均为h k A，故坐标系｛B｝的原点的位移也为＝h k A，两边与k A做点积可得

由式（2-45）可得

［I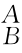－R kA（θ）］Q A＋h k A＝p

令Q A＝［qAxqAyqAz］T，代入上式可得

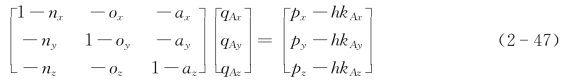
解上述方程组可求得点Q A。上述方程的解不唯一，这是因为直线l上的点均可作为式（2-43）中的点Q A。