如图2-8所示,刚体上一点Q,设它在坐标系{B}(与刚体固定连接)中的坐标为Bq=[Bq xBq yBqz]T,如果已知该时刻刚体的位置向量p AB=![]() =[pxpypz]T∈ℜ3和姿态矩阵
=[pxpypz]T∈ℜ3和姿态矩阵 R=[n o a]。此时,点Q在坐标系{A}中的坐标Aq=[Aq xAq yAqz]T如何确定?
R=[n o a]。此时,点Q在坐标系{A}中的坐标Aq=[Aq xAq yAqz]T如何确定?
由空间解析几何中的向量代数可知,只有同一个坐标系中的向量才能合成,如图2-8所示,在坐标系{A}中,根据向量合成的三角形法则可得
![]()
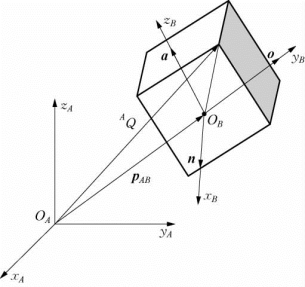
图2-8 点的坐标在两个坐标系之间的坐标变换
式中,![]() 表示图2-8中的向量
表示图2-8中的向量![]() 在坐标系{A}中的描述。向量
在坐标系{A}中的描述。向量![]() 在坐标系{B}中的描述为
在坐标系{B}中的描述为![]() =Bq,为已知量,现在需要确定向量
=Bq,为已知量,现在需要确定向量![]() 与向量
与向量![]() =Bq的关系,即同一个向量
=Bq的关系,即同一个向量![]() 在坐标系{A}中的坐标与在坐标系{B}中的坐标之间的关系。
在坐标系{A}中的坐标与在坐标系{B}中的坐标之间的关系。
由2.2.2节分析以及式(2-4)可知,沿着x B轴、y B轴和z B轴三个正方向的单位向量在坐标系{A}中分别为n、o、a,因而由式(2-12)可得向量![]() 在坐标系{A}中描述为
在坐标系{A}中描述为
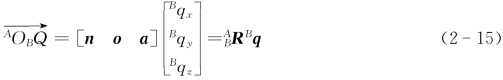
在坐标系{B}中,点Q的坐标为BQ=[BqxBq yBqz],即向量![]() 在坐标系{B}的x B轴、y B轴和z B轴上的投影分别为Bq x、Bq y、Bqz。将式(2-15)代入式(2-14),可得
在坐标系{B}的x B轴、y B轴和z B轴上的投影分别为Bq x、Bq y、Bqz。将式(2-15)代入式(2-14),可得
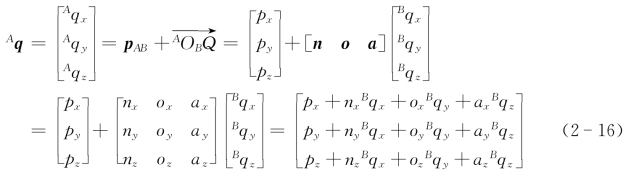
为便于运算,可引入齐次坐标,即点的坐标和向量的坐标由三阶矩阵(列向量)改变为四阶矩阵(列向量):
A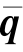 =[Aq 1]T=[Aq xAq yAqz1]TB
=[Aq 1]T=[Aq xAq yAqz1]TB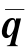 =[Bq 1]T=[BqxBq yBqz1]T
=[Bq 1]T=[BqxBq yBqz1]T
因为向量是其终点和起点的对应坐标差,故向量v的齐次坐标为
A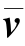 =[Av 0]T=[Av xAv yAv z0]TB
=[Av 0]T=[Av xAv yAv z0]TB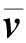 =[Bv 0]T=[Bv xBv yBv z0]T
=[Bv 0]T=[Bv xBv yBv z0]T
引入齐次坐标后,根据矩阵运算规则可得
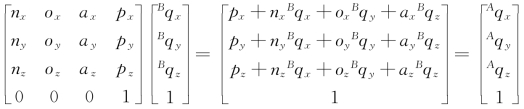
即
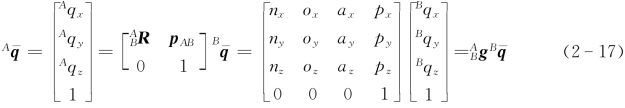
其中(www.daowen.com)
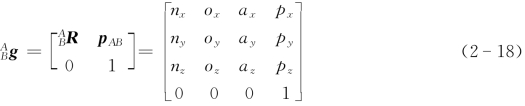
4×4矩阵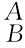 g包括坐标系{B}(刚体)相对于坐标系{A}的姿态矩阵
g包括坐标系{B}(刚体)相对于坐标系{A}的姿态矩阵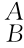 R,也包含坐标系{B}(刚体)相对于坐标系{A}的位置向量p AB,称
R,也包含坐标系{B}(刚体)相对于坐标系{A}的位置向量p AB,称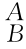 g为坐标系{B}(刚体)相对于坐标系{A}的位姿矩阵或位形矩阵。
g为坐标系{B}(刚体)相对于坐标系{A}的位姿矩阵或位形矩阵。
引入齐次坐标后,向量的齐次坐标变换表达式为
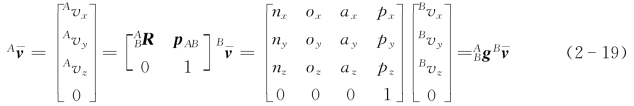
位姿矩阵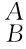 g的物理意义和作用是:
g的物理意义和作用是:
(1)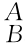 g表示坐标系{B}相对于坐标系{A}的位置和姿态。
g表示坐标系{B}相对于坐标系{A}的位置和姿态。
(2)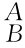 g可以把坐标系{B}中的向量和点的坐标变换到坐标系{A}中。
g可以把坐标系{B}中的向量和点的坐标变换到坐标系{A}中。
位姿矩阵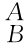 g是方阵,为求其行列式的值,按第四行展开可得
g是方阵,为求其行列式的值,按第四行展开可得
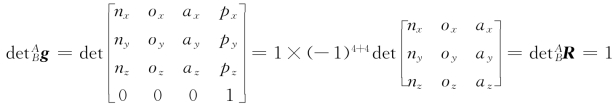
因而位姿矩阵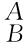 g是可逆矩阵(行列式的值不为0)。可以验证,
g是可逆矩阵(行列式的值不为0)。可以验证,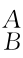 g的逆矩阵
g的逆矩阵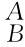 g-1为
g-1为
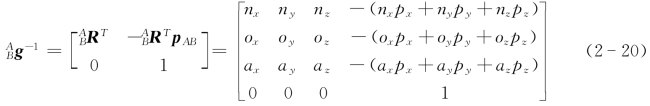
根据位姿矩阵的含义,可以确定任意三个坐标系{A}、{B}和{C}之间的位姿矩阵的关系。
如图2-9所示,已知坐标系{C}相对于坐标系{B}的位姿矩阵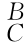 g和坐标系{B}相对于坐标系{A}的位姿矩阵
g和坐标系{B}相对于坐标系{A}的位姿矩阵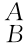 g,如何确定坐标系{C}相对于坐标系{A}的位姿?由于位姿矩阵
g,如何确定坐标系{C}相对于坐标系{A}的位姿?由于位姿矩阵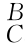 g的作用是把坐标系{C}中的向量和点的坐标变换到坐标系{B}中,而位姿矩阵
g的作用是把坐标系{C}中的向量和点的坐标变换到坐标系{B}中,而位姿矩阵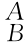 g的作用是把坐标系{B}中的向量和点的坐标变换到坐标系{A}中,故坐标系{C}相对于坐标系{A}的位姿矩阵
g的作用是把坐标系{B}中的向量和点的坐标变换到坐标系{A}中,故坐标系{C}相对于坐标系{A}的位姿矩阵 g为
g为
![]()
点Q在坐标系{C}和坐标系{A}之间的坐标变换为
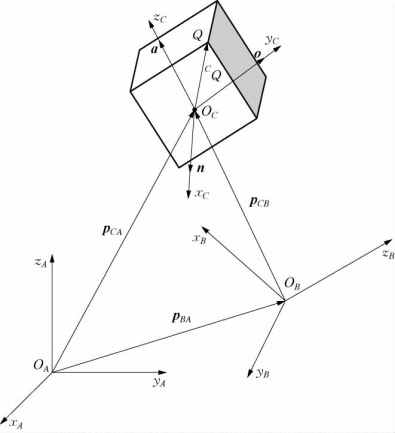
图2-9 刚体在不同坐标系之间的位姿变换
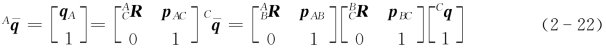
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





