由线性代数可知,一个自由向量v的坐标与选取的“基向量”相关,一旦“一组基向量”确定,则向量v在该基下的坐标便唯一确定,如图2-6所示。因而,对于同一向量,一旦“基向量”发生变化,则该向量的坐标也随之发生变化。
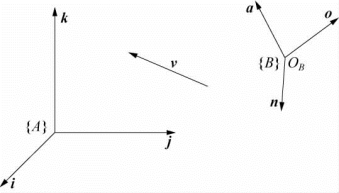
图2-6 向量在不同基下的坐标
由线性代数可知,在三维空间ℜ3中,任意三个线性无关的向量{γ1,γ2,γ3}都可以作为该向量空间的一组基。在研究机械运动时,一般取{γ1,γ2,γ3}为正交规范基(正交坐标系),即‖γ1‖=‖γ2‖=‖γ3‖=1,γ1·γ2=0,γ1·γ3=0,γ2·γ3=0,且γ3=γ1×γ2。如图2-6所示,设{i,j,k}是向量空间ℜ3的一组正交规范基,{n,o,a}是ℜ3的另外一组正交规范基。
按照“基”的定义,任意向量v都可以用“基”的线性组合来表示,则向量v可以分别表示成基{i,j,k}和基{n,o,a}的线性组合,即

式中,[l 1l 2l 3]T和[m1m2m3]T分别称为向量v在基{n,o,a}和基{i,j,k}下的坐标。
由于式(2-6)和式(2-7)表示的是同一个向量v,故v=[i j k]![]() =[n o a]
=[n o a]![]() ,因而
,因而

式(2-8)称为向量v由基{n,o,a}到基{i,j,k}的坐标变换。
由于向量n、o、a是三维空间的ℜ3中的向量,故n、o、a也可以由基{i,j,k}的线性组合来表示,即
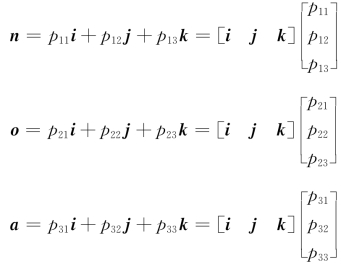
将上述三个表达式合写为

式中,矩阵P=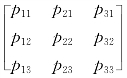 称为由基{i,j,k}到基{n,o,a}的过渡矩阵。过渡矩阵的三列元素[p 11p 12p 13]T、[p 21p 22p 23]T、[p 31p 32p 33]T分别表示向量n、o、a在基{i,j,k}下的坐标。当两组基向量{n,o,a}和{i,j,k}一旦取定,则过渡矩阵P便能唯一地确定,这是因为P=[i j k]-1[n o a]是唯一的。
称为由基{i,j,k}到基{n,o,a}的过渡矩阵。过渡矩阵的三列元素[p 11p 12p 13]T、[p 21p 22p 23]T、[p 31p 32p 33]T分别表示向量n、o、a在基{i,j,k}下的坐标。当两组基向量{n,o,a}和{i,j,k}一旦取定,则过渡矩阵P便能唯一地确定,这是因为P=[i j k]-1[n o a]是唯一的。
综上所述,在研究机械运动时,一般取基向量{n,o,a}和{i,j,k}为正交规范基,即正交坐标系。此时过渡矩阵的三列元素[p 11p 12p 13]T、[p 21p 22p 23]T、[p 31p 32p 33]T分别表示向量n、o、a在基坐标系{i j k}三个坐标轴i、j和k上的投影,也是向量n、o、a分别与i、j、k夹角的余弦值。对比式(2-4)可知,此时过渡矩阵P即为式(2-4)中的姿态矩阵R,即(https://www.daowen.com)
[n o a]=[i j k]P=[i j k]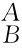 R (2-10)
R (2-10)
过渡矩阵 R的物理意义:由式(2-10)可知,在自然基下的某一时刻,由坐标系{A}到坐标系{B}的过渡矩阵P,即为坐标系{B}相对于坐标系{A}的姿态矩阵
R的物理意义:由式(2-10)可知,在自然基下的某一时刻,由坐标系{A}到坐标系{B}的过渡矩阵P,即为坐标系{B}相对于坐标系{A}的姿态矩阵 R。
R。
将式(2-10)代入式(2-8),可得

式(2-11)称为向量v由基{n,o,a}下的坐标[l1,l2,l3]到基{i,j,k}下的坐标[m1,m2,m3]之间的坐标变换矩阵。
如图2-7所示,若已知任意向量v在坐标系{B}中坐标为Bv=[Bv xBv yBv z]T以及坐标系{B}相对于坐标系{A}的姿态矩阵为 R=[n o a],则向量v在坐标系{A}中坐标Av如何确定?
R=[n o a],则向量v在坐标系{A}中坐标Av如何确定?
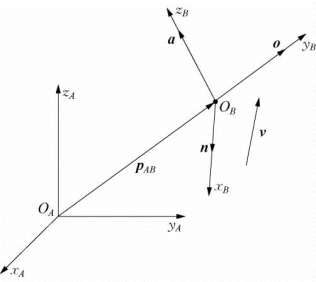
图2-7 向量v在两个坐标系之间的坐标变换
由图2-7可知,在坐标系{B}中,沿xB轴、y B轴和zB轴三个正方向的单位向量分别为[1 0 0]T、[0 1 0]T、[0 0 1]T,设它们在坐标系{A}中分别为n、o、a,而向量v在坐标系{B}中x B轴、y B轴和z B轴上的投影分别为Bv x、Bv y、Bv z,故向量v在三个正交的向量为n、o、a上的分向量分别为Bv xn、Bv yo和Bv za;因为向量n、o、a是以坐标系{A}中的x A轴、y A轴和z A轴三个正方向的单位向量作为“基向量”描述的,即它们是坐标系{A}中向量,故根据向量合成与分解法则,ℜ3空间中的任何一个向量都可以由该空间中的任意三个正交的分向量之和表示,即

式(2-12)与式(2-11)结果一致。由式(2-12)可知:若已知向量v在坐标系{B}中的坐标Bv=[Bv xBv yBv z]T以及坐标系{B}相对于坐标系{A}的姿态矩阵为 R,则向量v在坐标系{A}中的坐标Av=[Av xAv yAv z]T为姿态矩阵
R,则向量v在坐标系{A}中的坐标Av=[Av xAv yAv z]T为姿态矩阵 R“左乘”Bv。该结论具有一般性,可以推广到任意一个向量在任意两个坐标系{A}和{B}之间的坐标变换。
R“左乘”Bv。该结论具有一般性,可以推广到任意一个向量在任意两个坐标系{A}和{B}之间的坐标变换。
如图2-3所示,一旦刚体上的坐标系{B}的原点OB的位置向量p AB=![]() =[pxpypz]T∈ℜ3已知,同时坐标系{B}相对于坐标系{A}的姿态矩阵
=[pxpypz]T∈ℜ3已知,同时坐标系{B}相对于坐标系{A}的姿态矩阵 R[式(2-4)]已知,则刚体相对于坐标系{A}的位置和方向便完全且唯一地确定。
R[式(2-4)]已知,则刚体相对于坐标系{A}的位置和方向便完全且唯一地确定。
姿态矩阵 R逆矩阵
R逆矩阵 R-1的物理意义:坐标系{B}相对于坐标系{A}的姿态矩阵
R-1的物理意义:坐标系{B}相对于坐标系{A}的姿态矩阵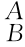 R的逆阵
R的逆阵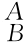 R-1=
R-1= R T即为坐标系{A}相对于坐标系{B}的姿态矩阵
R T即为坐标系{A}相对于坐标系{B}的姿态矩阵 R,证明过程如下:
R,证明过程如下:
由式(2-9)可知:[n o a]=[i j k]P=[i j k]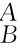 R,故
R,故
![]()
按照定义, R T是由基{n,o,a}到{i,j,k}的过渡矩阵,按照式(2-10)所示的过渡矩阵的物理意义,由于{n,o,a}和{i,j,k}是自然基,
R T是由基{n,o,a}到{i,j,k}的过渡矩阵,按照式(2-10)所示的过渡矩阵的物理意义,由于{n,o,a}和{i,j,k}是自然基, R T即为坐标系{A}相对于坐标系{B}的姿态矩阵
R T即为坐标系{A}相对于坐标系{B}的姿态矩阵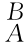 R。
R。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







