为了确定刚体的位置和姿态,需要在刚体上建立一个与刚体“固定”连接的坐标系{B},如图2-3所示。刚体的运动,包括平动和转动,可由位置和姿态的变化来体现。具体而言,平动和转动可以由坐标系{B}与坐标系{A}之间的关系变化来确定。

图2-3 刚体的位置、姿态与坐标系的关系
如图2-3所示,由于物体在三维欧氏空间ℜ3中运动,坐标系{B}的原点OB在欧氏空间ℜ3中的位置向量由3×1矩阵p AB![]() =[p xp ypz]T∈ℜ3表示,它完全确定了刚体在某一时刻的位置。
=[p xp ypz]T∈ℜ3表示,它完全确定了刚体在某一时刻的位置。
刚体的姿态反映的是刚体与坐标系{A}的三个坐标轴x A、y A、z A之间的方向,也就是刚体与坐标系{A}的三个坐标轴之间的角度关系,它可由坐标系{B}的三个坐标轴x B、y B、z B与坐标系{A}的三个坐标轴x A、y A、z A之间的夹角确定。为此,需要研究如何确定两个向量的夹角。
由高等数学中的解析几何和向量代数相关理论可知,对于空间中的任意两个向量p、q,它们在坐标系中的三个坐标轴上的投影(px,py,pz)和(qx,qy,qz),若满足px/qx=py/qy=pz/qz,则向量p和q平行,即p∥q确定。这表明一个向量p的方向可以由它在坐标轴上的投影(px,py,pz)唯一确定,如图2-4a所示。

图2-4 向量在坐标轴上的投影
可以应用空间解析几何和向量代数中向量点积的定义求向量p在q的投影。p和q的点积为p·q=‖p‖‖q‖cosθ,其中:‖p‖和‖q‖分别为向量p和q的模;θ为向量p和q的夹角,如图2-4b所示。当‖q‖=1,‖p‖=1时,向量p在q上的投影为p·q=‖p‖‖q‖cosθ=cosθ,即单位向量p在向量q上的投影为向量p和q的夹角θ的余弦值cosθ。如图2-4c所示,向量p的单位向量e在三个坐标轴上的投影为[cosα cosβ cosγ]T,其中cosα、cosβ和cosγ分别为向量p与坐标轴x、y、z夹角的余弦值,由[cosα cosβ cosγ]T可以完全确定向量p的方向。设p与坐标轴x、y、z夹角分别为∠p x、∠p y和∠p z,则向量p在坐标系{x Ay Az A}中的方向向量为

向量p的方向由向量p与坐标轴x、y、z夹角的余弦值cos∠p x、cos∠p y、cos∠p z唯一决定,即由p的单位向量e在坐标轴x、y、z投影唯一决定。
如图2-3所示,沿着坐标系{B}的三个坐标轴x B、y B、z B的正方向分别取三个单位向量,它们在坐标系{B}中分别为e1=[1 0 0],e2=[0 1 0],e3=[0 0 1],设这三个单位向量在坐标系{A}中分别为n、o、a。以向量n为例,设它在坐标系{A}的三个坐标轴x A、y A、z A上的投影分别为n x、ny、nz。由式(2-3)可得:nx=cos∠n x A,ny=cos∠n x Y,nz=cos∠n x Z,把它们合并成一个列向量为An=[An xAn yAn z]T;同理,向量o和a在坐标系{A}的三个坐标轴x A、y A、z A的投影写成列向量分别为Ao=[Ao xAo yAo z]T和Aa=[AaxAa yAaz]T。An=[AnxAn yAnz]T、Ao=[AoxAoyAoz]T和Aa=[AaxAayAaz]T可以合并成一个3×3矩阵 R,即
R,即
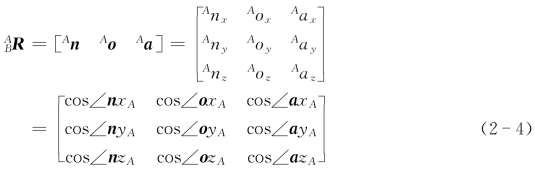
上述矩阵 R称为刚体的姿态矩阵,因为它完全确定了刚体(坐标系{B})在某一时刻相对于坐标系{A}的方向。根据欧拉定理,姿态矩阵
R称为刚体的姿态矩阵,因为它完全确定了刚体(坐标系{B})在某一时刻相对于坐标系{A}的方向。根据欧拉定理,姿态矩阵 R与将坐标系{A}沿某个轴旋转一定角度以使得它与坐标系{B}重合所对应的刚体变换相等,因此矩阵
R与将坐标系{A}沿某个轴旋转一定角度以使得它与坐标系{B}重合所对应的刚体变换相等,因此矩阵 R又称旋转矩阵。(https://www.daowen.com)
R又称旋转矩阵。(https://www.daowen.com)
旋转矩阵(姿态矩阵) R具有如下性质:
R具有如下性质:
(1)由于采用正交坐标系,如图2-5a所示,x B、y B、zB三个方向向量n、o、a相互正交,即向量点积为0:n·o=o·n=0,n·a=a·n=0,o·a=a·o=0。
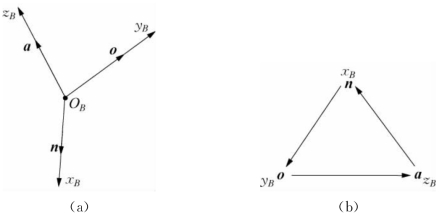
图2-5 右手正交坐标系三个坐标轴之间的关系
(2)由于采用右手坐标系,如图2-5b所示,x B、y B、z B三个方向向量n、o、a满足如下叉积运算(沿逆时针方向):n=o×a;o=a×n;a=n×o。
(3)n·n=1;o·o=1;a·a=1。
(4)向量n、o、a并不相互独立,由旋转矩阵的性质(1)和(2)可知,一旦其中两个向量已知,则第三个向量可根据另外两个向量的叉积运算确定。
(5)姿态矩阵 R是正交矩阵,即满足
R是正交矩阵,即满足 R(
R( R)T=(
R)T=( R)
R)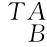 R=
R= =I。该性质可以在上述矩阵运算过程中,利用性质(1)、(2)和(3)证明。
=I。该性质可以在上述矩阵运算过程中,利用性质(1)、(2)和(3)证明。
(6)矩阵 R的行列式值为+1,即det
R的行列式值为+1,即det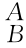 R=
R= =1。该性质可以利用det
=1。该性质可以利用det R=(n×o)·a=a·a=1证明。
R=(n×o)·a=a·a=1证明。
所有满足上述性质(1)和(2)的矩阵R的集合用SO(3)表示(special orthogonal),即SO(3)={R∈ℜ3×ℜ3:RR T=R TR=I,det R=+1}。
姿态矩阵可以用于描述刚体姿态,即坐标系的姿态。
式(2-4)所示的姿态矩阵 R的3列[AnxAnyAnz]T、[AoxAoyAoz]T和[AaxAayAaz]T分别表示坐标系{B}的3个坐标轴x B、y B、z B上的3个单位向量n、o、a在坐标系{A}的3个坐标轴x A、y A、z A上的投影,即单位向量n、o、a与坐标系{A}的3个轴x A、y A、z A夹角的余弦。姿态矩阵完全确定了刚体上的坐标系{B}的3个坐标轴x B、y B、z B相对于坐标系{A}的3个轴x A、y A、z A的角位移,即描述了刚体相对于坐标系{A}的旋转运动。
R的3列[AnxAnyAnz]T、[AoxAoyAoz]T和[AaxAayAaz]T分别表示坐标系{B}的3个坐标轴x B、y B、z B上的3个单位向量n、o、a在坐标系{A}的3个坐标轴x A、y A、z A上的投影,即单位向量n、o、a与坐标系{A}的3个轴x A、y A、z A夹角的余弦。姿态矩阵完全确定了刚体上的坐标系{B}的3个坐标轴x B、y B、z B相对于坐标系{A}的3个轴x A、y A、z A的角位移,即描述了刚体相对于坐标系{A}的旋转运动。
若已知 R,则可以证明坐标系{A}相对于坐标系{B}的姿态
R,则可以证明坐标系{A}相对于坐标系{B}的姿态 R为
R为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






