3.3.2.1　仿真涉及的分析技术方法介绍

针对EFP 型地雷爆炸成形及对目标靶板的侵彻，采用MSC.Dytran 的多物质欧拉技术进行数值仿真分析；针对爆破型地雷对目标靶板及带有假人的方舱结构的爆炸作用仿真，采用MSC.Dytran 的流固耦合技术进行数值仿真分析。

MSC.Dytran 是一种用于分析结构及流体材料的非线性动态行为的数值仿真程序，该程序适用于分析包含大变形、高度非线性和复杂的动态边界条件的短暂的动力学过程。软件提供拉格朗日求解器与欧拉求解器，因而既能模拟结构又能模拟流体。拉格朗日网格与欧拉网格之间可以进行耦合，从而可以分析流体与结构之间的相互作用，形成精确独特的流固耦合技术。

1.MSC.Dytran 的欧拉方法

欧拉方法主要用于流体流动问题的分析以及固体材料发生很大变形的情况。当采用欧拉方法时，节点固定在空间中，由相关节点连接而成的单元仅仅是空间的划分。欧拉网格是一个固定的参照系，分析对象的材料在网格中流动，材料的质量、动量以及能量从一个元素流向另一个元素。因此，欧拉法计算的是材料在体积恒定的元素中的运动。应当注意的是MSC.Dytran 中欧拉网格与拉格朗日网格采用同样的方式来定义，网格可以具有任意形状，这样比其他一些仅仅采用矩形网格的欧拉方法的程序要灵活得多。

不过，必须记住欧拉网格与拉格朗日网格用法不同。在建立欧拉网格时最重要的问题是要让网格足够大以能够容纳变形后的全体材料。欧拉网格的作用类似于一个容器，除非专门定义，否则材料不能流出网格。如果网格太小，容易引起应力波反射和压力堆积。

MSC.Dytran 中的欧拉求解器在空间域的离散上采用控制容积法，在时间域的离散上采用时间积分法。程序采用的基本单元为八节点的任意六面体单元，此外还有六节点的任意三棱柱单元及四节点的任意四面体单元。单元中可以充满材料，也可以是空的，或者有一部分空间有材料。同时，一个单元中可以同时有几种材料。材料可以是理想流体，也可以是非理想流体。

一般流体动力学问题需要满足如下控制方程：

·质量守恒方程；

·动量守恒方程；

·能量守恒方程；

·状态方程。

对于非理想流体，还要满足本构方程。

MSC.Dytran 的欧拉求解器采用控制容积法和时间积分做材料流动的分析，具体方法如下：

将控制方程在流场中任一封闭曲面所包含的容积内进行积分，得到积分形式的控制方程：

质量守恒

动量守恒

能量守恒

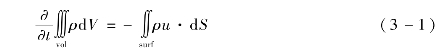
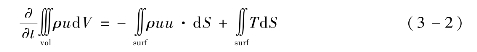
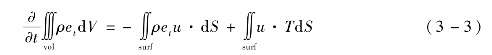
将以上方程乘以时间积分的时间步长，可以得到该时间步长内的变化量关系：

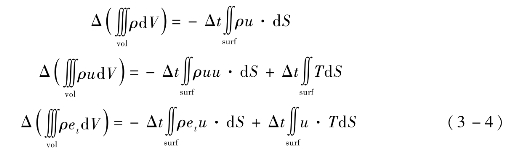
将每一个单元作为一个封闭体应用以上关系式，得出从时刻tn 到tn+1 的变化量关系：

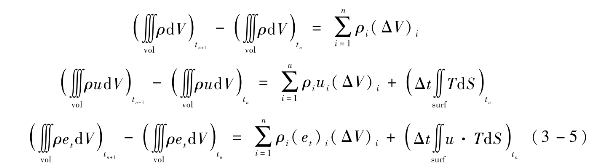
式中，n 为单元的表面数目；（ΔV）i 为从时刻tn 到tn+1 的一个时间步长内穿越该单元的第i 个表面的体积流量；ρi（ΔV）i 为相应的质量流量；ρiui（ΔV）i 为相应的动量流量；ρi（et）i（ΔV）i 为相应的能量流量。在tn 时刻的各物理参数已知的情况下，用相邻元素形心处的流速进行线性插值，可以得出元素边界面处的流速：

然后用施主法可以计算出穿越单元表面的质量、动量及能量的流量：

采用单点高斯积分，可以将以上控制方程中左边的体积分表示为有关物理量（密度、流速、内能等）的线性函数，代入控制方程得到关于单元形心处的各物理量在tn+1时刻的值的线性方程：

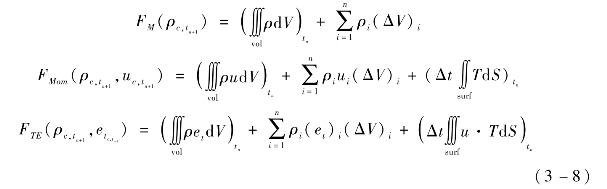
从而可以解出单元形心处的物理量在tn+1时刻的值。

2.欧拉-拉格朗日耦合

拉格朗日网格和欧拉网格可以用在同一个分析模型中，并且可以通过一个界面相互耦合。该界面是欧拉网格中的材料的流场边界，同时欧拉网格中的材料对界面产生作用力，使拉格朗日发生变形。MSC.Dytran 中的耦合方式有两种：一般耦合（General Coupling）和任意拉格朗日- 欧拉耦合（ALE）。ALE的特别之处在于，欧拉网格可以移动。当结构变形时，耦合界面的位置和形状也发生变化，界面上的欧拉网格节点发生相应的移动，带动欧拉网格的其余部分跟着运动，其运动的方式可由用户确定。因此，在ALE 耦合计算中，一方面材料在欧拉网格中移动，另一方面，欧拉网格节点本身也在运动，使欧拉网格的位置和形状在不断调整。

本项目采用一般耦合进行爆破型地雷对目标结构的冲击损伤分析。MSC.Dytran 程序中欧拉求解器与拉格朗日求解器是分开的，如果不定义它们之间的耦合关系，即使拉格朗日单元处于欧拉网格的范围之内，也不会对欧拉材料的流动产生任何影响，同时拉格朗日单元也不会受到来自欧拉材料的压力的作用。为此程序在结构网格和流体网格之间定义一般耦合面（General Coupling Surface）以分析它们之间的流固耦合作用，如图3-25所示。

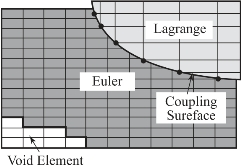
图3-25　一般耦合算法

欧拉网格和拉格朗日网格之间的相互作用力通过这层耦合面互相传递，对于欧拉网格，它充当流场的边界。因为划分圆柱壳的壳单元本身就构成了一个封闭的面，所以可以利用该封闭面作为一般耦合面。定义一般耦合算法的优点在于在建立有限元模型时，可以不必过多考虑欧拉单元与拉格朗日单元之间的相互匹配，因而简化了建模的过程。为防止冲击波的反射和压力堆积，必须在流体边界定义穿透边界，使得流体介质能够流出。

一般耦合大多是拉格朗日的固体在欧拉的流场范围内运动，即拉格朗日域驱动欧拉域；流场虽有速度，但代表流场的欧拉网格固定在空间及不受拉格朗日的固体影响。换言之，流固耦合过程中，欧拉网格不移动，也不变形。一般耦合计算的前处理大多用封闭的dummy shell 耦合面隔开拉格朗日域和欧拉域；当开始计算时，拉格朗日的固体需要在欧拉域的范围内有重叠，且固体、流体或两者有运动，以启动流固耦合计算。若拉格朗日域与欧拉域毫无重叠，则无法起动流固耦合计算。当然，拉格朗日的固体可完全位于欧拉域内，不因拉格朗日的固体运动而使欧拉网格移动或变形。此外，一般耦合也可应用于具有不规则的固定固体边界的流场模拟计算，即将不动的固体边界与流场的关联视为流固耦合现象。

3.接触算法

在经典的有限元方法中，结构之间的相互作用要有网格的连贯性作为保障。这就使经典有限元方法能很好地处理结构小变形问题，但是很难处理大变形问题，以及网格不连贯、结构之间相离的问题。

MSC.Dytran 程序中的接触面模型提供了一个非常简单方便的模拟拉格朗日模型各部分之间相互作用的手段。运用接触面模型，能够模拟可变形体或刚性体之间的连续接触。接触面模型与以前的间隙元模型相比较，不仅收敛性大大增强，而且使相互接触的两个物体可以做大距离的相对移动。

接触面一共有三种类型：

两个面之间的任意接触；

单个面自身的接触；

若干离散节点与一个面之间的接触。

这几种类型的接触均是通过CONTACT 卡来定义，定义时在卡片上相应的位置确定接触的类型，以及其他有关的参数。

两个面之间的任意接触是最常用到的一种情况，用来模拟两个面之间的接触、分离，并且允许两个面之间具有摩擦系数。

（1）面段与面。

为了定义接触，必须先定义发生接触的面（SURFACE）。面的定义通过确定处于面上的单元的表面（FACE）来实现。每个单元的表面被称作“面段”（SEGMENT），是组成面的单位，是一种几何单元而非物理单元，但与物理单元一样，也是由节点连接而成的。面段通过CSEG、CFACE 或CFACE1 卡来定义。面段可以附连在体元或壳元上，可以是四边形或三角形。

相互接触的两个面，其地位是不相等的，一个被称为“主面”，另一个被称为“从属面”。每个面都是由面段集组成的。这两个面必须相互分开。一个面段不能同时属于主面和从属面，如图3-26所示。

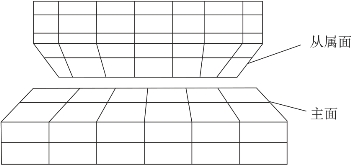
图3-26　主面和从属面关系图

面段的定义有多种方法。可以使用CSEG、CFACE 及CFACE1 等卡片来定义，也可通过面段所依附的壳元或膜元来定义，而CSEG 卡的定义也可以通过CQUAD4 与CTRIA3 的形式来代替。每种方法具体如下：

CSEG：在CSEG 卡上顺序填写连接起来形成面段的节点的编号。

CFACE：在CFACE 卡上确定面段依附的单元号及单元表面编号。

CFACE1：在CFACE1 卡上确定面段依附的单元号，与CFACE 不同的是，通过确定单元表面上的节点编号来确定表面，而不是直接确定表面编号。

CQUAD4 与CTRIA3 的形式定义CSEG：将单元的性质卡号设置为9999 或Dummy。

组成面的面段集的确定也有多种方法：

·确定面段集的集号。每个面段在CSEG、CFACE 或CFACE1 卡上都有集号的定义。如果是用CQUAD4 或CTRIA3 的形式定义的，则性质卡号就是集号。

·直接引用二维物理单元CQUAD4 或CTRIA3 的集。有三种方法：根据单元号；根据材料卡号；根据性质卡号。

与二维单元一样，面段的节点连接顺序很重要，决定了局部坐标系的方向，以及接触的方向。组成面的面段，其法线应当指向同一个方向，否则会有问题。接触关系定义卡CONTACT 上可以设定面段法线的方向，据此程序会自动将组成一个面的面段的法线方向统一。发生接触的两个面的方向最好相互指向对方，或相互背离对方，这时CONTACT 卡上的SIDE 域（发生接触的一侧）填写TOP 或BOTTOM，否则必须填写BOTH，而这容易引起问题。

面段与面是MSC.Dytran 中的重要建模工具，不仅用于接触面，而且流固耦合的界面、流场边界面等均使用它们来建模。

（2）穿透问题。

两个接触面不能有初始的相互穿透，必须相切或相隔一段距离。如果接触面有初始穿透，程序在计算之前的检查中会发现并发出警告信息。但这时计算仍会进行下去，在接触面之间产生很大的相互作用力，以使它们相互分开。穿透量太大，作用力很大，则会出现问题。

CONTACT 卡上的PENTOL 域定义初始穿透检查的容差。容差范围之外的节点不参加接触计算。

（3）计算方法。

关于接触问题的计算方法的理论本书不做详细介绍。但是对计算原理做一点了解是十分必要的，因为这有助于正确、有效地使用接触模型。接触问题的计算步骤大致是这样的：在每一个时间步，程序检查从属面上的每一个节点，首先找出距离该点最近的主面面段，看节点是否穿透了该面段。如果没有，计算继续进行。如果已经穿透，程序将在垂直于主面的方向上施加作用力阻止进一步穿透的发生。作用力的大小取决于穿透量的大小以及接触处的双方单元的特性。程序内部根据在保持计算稳定的条件下使穿透量最小的原则计算作用力的大小。CONTACT 卡上的FACT 域可以定义作用力大小的放大系数。如果发生接触的两部件被很大的作用力压在一起，该系数就很有用。不过，太大的系数会带来计算不稳定的问题。

接触面之间可以有摩擦力。摩擦力的大小等于摩擦系数乘以法向接触力。摩擦力的方向与接触面的相对运动方向相反。

摩擦系数的计算按照以下公式：

式中，μs=静摩擦系数；

μk=动摩擦系数；

β =指数衰减系数；

v=主从面之间的相对滑行速度。

用户需要确定的参数为μs，μk 及β。

接触算法是不对称的。程序针对每个从属面节点检查其是否穿透主面，但反过来却并不检查主面节点是否穿透从属面。因此，从属面的网格应当比主面网格细，否则会发生出现穿透而程序未能检查出来的问题，这将引起沙漏现象或错误的计算结果。

由于距离每个从属面节点的主面面段在计算过程中不断更新，所以即使接触面发生大变形或大相对位移，接触问题的计算也不受影响。

（4）计算精度与效率。

一般来讲，接触面使用起来非常简单，计算效率也高。但穿透检查很费时间，因此接触面的定义应当局限于那些有可能发生接触的地方，以尽量减少面段数量。

CONTACT 卡上的UPDATE 域及SORT 域用来控制接触算法，调节计算精度与计算工作量。UPDATE 决定对接触力进行更新的频率。分析的问题可以当作是静态的，在分析过程中接触力几乎保持恒定。在这种情况下，接触力不需要每个时间步长都重新计算。

这样可以节省计算时间。如果所分析的问题动态性很强，则接触力的更新应当很频繁。SORT 域决定与从属面节点对应的主面面段的更新的频率。与UPDATE 一样，取什么值取决于问题的动态性。

TSTART 与TEND 分别定义接触关系定义的打开与关闭时间。这使得程序可以只在需要考虑接触问题时进行搜寻最近面段、检查穿透等耗费时间的运算。如果采用缺省值，则接触关系在整个分析过程中一直起作用。

单面自身接触与双面相互接触是相类似的。只不过这里不定义主面和从属面，而是定义不能穿透自身的从属面。这对于结构发生屈曲、弯折，与自身相碰的情况尤其有用。因为这时结构表面哪一部分与哪一部分相碰事先无法确定，从而只能将整个表面定义为自身接触的单一接触面。

单一接触面的定义同样使用CONTACT 卡，只不过只需要定义从属面，定义主面的域留为空白。单一接触面也可具有摩擦力，其计算方法与双面接触一样。

与双面接触不同的是，面段的节点连接顺序无关紧要。接触发生在哪一侧程序能够自动判别。接触面面段的法向应当指向同一方向。不过如果用户建立的模型中接触面网格的方向不符合这一要求，只要在CONTACT 卡上打开REVERSE 功能，程序能够自动将网格方向调整好。

单面接触与双面接触的算法是一样的。而且单面情况计算尤其快，所定义的接触范围可以很广。

4.某型EFP 地雷爆炸成形过程仿真研究

爆炸成形弹丸（Explosively Formed Penetrator，简称EFP）是一种反装甲目标的战斗部。自20世纪60年代开始应用于武器弹药以来，一直受到美国、俄罗斯等军事强国的重视，广泛应用于反舰导弹、末敏弹、反坦克智能雷和反坦克车底地雷等反装甲弹药上。爆炸成形弹丸的形成机理非常复杂，影响因素很多。对于等壁厚球缺型药型罩的EFP 成形，在各种影响因素中，装药长径比、药型罩曲率半径、药型罩壁厚、壳体厚度是影响EFP 成形性能的重要因素。早期大多采用实验研究方法。进入20世纪80年代后期，随着计算机软、硬件技术的不断发展，以及人们对于材料在大变形、高应变率、高温、高压下动态行为的认识更加深入，计算机仿真在爆炸成形弹丸战斗部设计中发挥出更大的作用，国内外学者将计算机仿真与非线性优化数学方法相结合开展了爆炸成形弹丸战斗部的优化设计。图3-27 为EFP 典型成形过程的示意图。

图3-27　爆炸成形弹丸示意图

本节内容仿真采用多物质欧拉法，针对大锥形药型罩装药结构的某型EFP反坦克车底地雷，建立该型地雷的仿真模型，对起爆、药型罩翻转成形过程进行模拟，要求仿真计算EFP 弹丸及头部的速度时间曲线及具体成形状态。

3.3.2.2　模型介绍

本项目拟仿真的某型EFP 地雷结构，主要由炸药、药型罩和壳体组成。炸药为钝化黑索今，有效药量为0.78kg，装药高度和直径分别为82mm、95mm，药型罩选用紫铜，形状为等壁厚大锥角圆锥罩，锥度为120°，壳体为钢材料。

采用多物质欧拉法模拟EFP 战斗部爆炸成形过程，多物质欧拉法适合模拟弹丸成形过程中的大变形，能够很好地模拟弹丸的加速和成形过程。由于地雷是圆柱形，具有轴对称性，为了减少计算量，EFP 地雷仿真模型设置为1/2 模型，如图3-28所示。

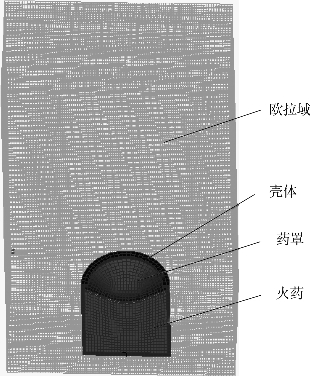
图3-28　EFP 地雷模型

1.欧拉域模型

欧拉域是物质运动的空间，采用多层填充法实现多物质定义，即在不同的空间填充不同的物质，若在相同的空间填充两种以上的物质，则最后一层填充物起作用。欧拉域采用长方体体单元建模，定义PEULER1MMSTREN 属性。最初的填充物为理想空气，通过理想气体状态方程描述空气。选用MSC.Dytran 的Idea-Gas（DMAT）Eulersolid 材料卡为空气建模。

欧拉域的网格如图3-29所示。

2.壳体、药罩模型

壳体、药罩材料表面划分常规壳元，定义dummy shell 属性，壳元围成的封闭空间填充欧拉材料。选用MSC.Dytran 的ElasPlas（DMAT）Eulersolid 材料卡。

壳体、药罩材料表面网格如图3-30所示。

图3-29　欧拉网格

图3-30　壳体、药罩表面网格

3.炸药模型

炸药表面划分常规壳元，定义dummy shell 属性，壳元围成的封闭空间填充欧拉材料。选用MSC.Dytran 的JWL 状态方程描述炸药爆轰过程。

炸药表面网格如图3-31所示。

图3-31　炸药表面网格

3.3.2.3　材料模型介绍

本项目对于理想空气的模拟，采用理想气体状态方程模拟，即γ 律状态方程EOSGAM。EOSGAM 模型定义气体的γ 律状态方程中，压力是密度、比内能及理想气体比热容比γ 的函数：

式中，e 为单位质量的内能；ρ 为总体材料密度；γ 为比热容比（Cp/Cν）。

理想空气材料卡片如图3-32所示。

3.3.2.4　炸药材料卡

本项目对于炸药的模拟，采用JWL 状态方程，JWL 状态方程EOSJWL如下：

式中，p 为爆压；η =ρ/ρ0；e 为单位质量的内能；ρ0 为参考密度；ρ 为总体材料密度；A，B，ω，R1 及R2 为常数。

因此，为准确计算炸药爆轰需提供以下参数：

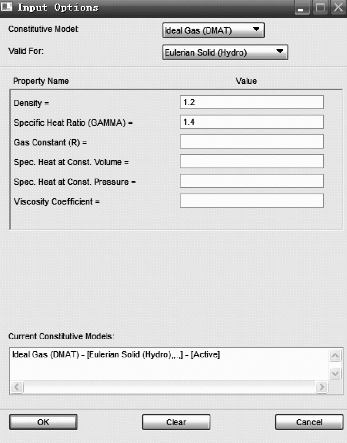
图3-32　理想气体材料卡片

·炸药名称及炸药药柱形状；

·装药密度；

·JWL 状态方程常数A、B、ω、R1 及R2，起爆点，爆速及爆压。

钝化黑索今炸药材料卡片如图3-33所示。(www.daowen.com)

1.药罩材料卡

本项目对于药罩的模拟，采用状态方程/弹塑性本构描述材料在高压下的大变形行为。药罩结构材料采用多项式状态方程本构，并采用Johnson- Cook屈服模式，用来描述金属材料在大变形、高应变率和高温条件下的本构关系，相应公式如下：

对于多项式状态方程，其压力是相对体积及比内能的多项式函数。

压缩状态（μ ＞0）：

拉伸状态（μ≤0）：

式中，μ=η-1；η=ρ/ρ0；ρ 为总体材料密度；ρ0 为参考密度；e 为单位质量内能。

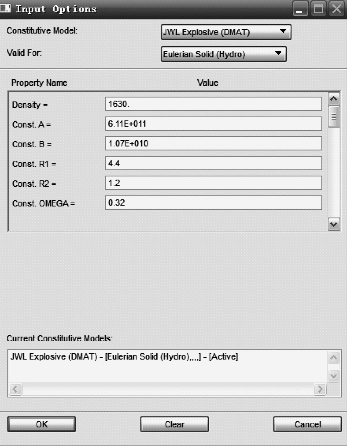
图3-33　炸药材料卡片

Johnson-Cook 屈服模式：

式中，A、B、n、C 和m 为材料常数，A 为材料在准静态下的屈服强度，B 和n为应变硬化的影响，C 为应变率敏感指数，m 为温度软化系数；T* =（T-Tr）/（Tm-Tr）；εp 为等效塑性应变； 为参考应变率；T 为温度；Tr 为室温；Tm 为融化温度。

因此，准确模拟该类结构在爆轰作用下的破坏需要以下材料参数：

·材料密度、杨式模量、泊松比、体积模量；

·多项式参数a1、a2、a3、b0、b1、b2、b3；

·屈服应力、抗拉强度、延伸率；

·强化系数B；

·硬化指数n；

·应变率参数c；

·参考应变率；

·比热容；

·融化温度Tm；

·等效刚度、泊松比、屈服应力、抗拉强度或失效最大塑性应力应变等。

紫铜药罩的材料卡片如图3-34所示。

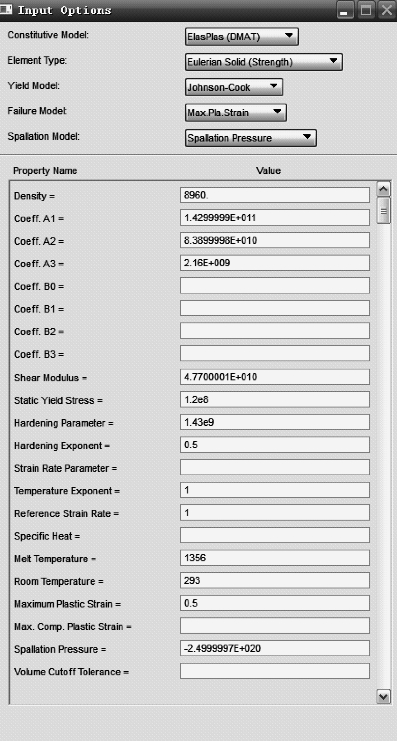
图3-34　紫铜材料卡片

2.壳体材料卡

本项目对于壳体的模拟，采用状态方程/弹塑性本构描述材料在高压下的大变形行为。壳体结构材料采用多项式状态方程本构，并采用冯·米塞斯屈服模型YLDVM。

壳体状态方程如下所述。

壳体屈服模式采用冯·米塞斯屈服模型YLDVM，如下：

YLDVM 卡用来定义冯·米塞斯屈服模型。通过确定一条双线性或分段线性的应力-应变曲线，定义材料的屈服应力和强化模量。对于拉格朗日及欧拉体元，只能采用弹性理想塑性模型。

双线性应力-应变曲线（图3-35）屈服应力按以下公式计算：

式中，σ0 为屈服应力；E 为杨氏模量；Eh 为强化模量；εp 为等效塑性应变。

分段线性曲线如图3-36所示。

图3-35　双线性应力-应变曲线

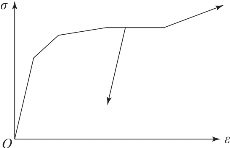
图3-36　分段线性曲线

在每一步时间积分的计算中，根据应变值通过插值法计算应力值：

其中σj 与εj 为定义分段线性曲线的表格函数的节点值。在MSC.Dytran 程序内部，应力-应变关系采用真实应力对应等效应变的方式来表示。但为了方便起见，在输入时，可以采用以下方式：

·真实应力/真实应变

·工程应力/工程应变

·真实应力/塑性应变

·真实应力/塑性模量

真实应力定义为：

式中，F 为当前的力；A 为当前的面积。

塑性应变εpl定义为：

而工程应变定义为：

式中，A0 为初始面积；I0 为初始长度。

真实应力/真实应变与工程应力/工程应变之间的关系如下：

在小应变状态，工程应力-应变与真实应力- 应变差别不大。然而，在应变较大时，差别不可忽视，这时需要确保输入正确的应力-应变关系。

壳体A3 钢材料卡如图3-37所示。

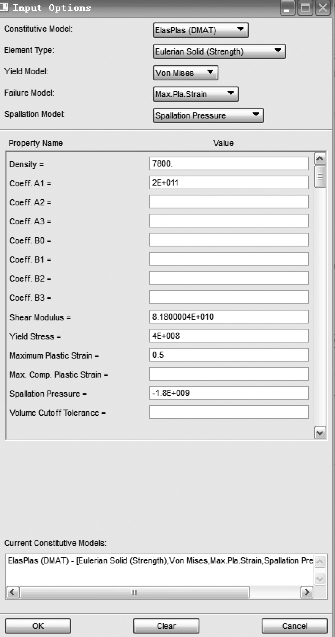
图3-37　壳体A3 钢材料卡

3.3.2.5　载荷及边界条件介绍

欧拉单元的初始状态可以用TICEL 或TICEUL 来定义。这是用来设定模型在分析开始时的状态，此后的状态由计算确定。

TICEL 卡用来定义单元的初始状态。任何单元物理量都可以赋予一定的初始值。TICEUL 卡用来针对欧拉网格中的几何区域定义初始状态。TICEUL 必须与EULER1 卡配合使用。几何区域可以是圆柱形或球形，也可以是由某个单元集构成的。每个几何区域都有一个级别号。当两个区域相互覆盖时，它们的公共区域的初始值的定义以级别号较高的几何区域为准。利用若干不同级别号、不同形状的几何区域相互覆盖，可以构造出形状较为复杂的几何区域用于初始状态的定义。相同级别号的区域不能相互覆盖，否则会发生错误。

初始条件定义的步骤如图3-38所示。

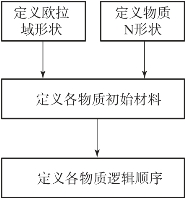
图3-38　初始条件定义步骤

欧拉域初始形状定义为球形，如图3-39所示。

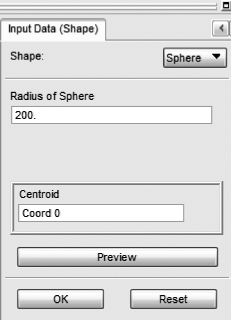
图3-39　欧拉域初始形状定义

药罩初始形状由药罩表面dummy shell 单元确定，药罩初始形状定义如图3-40所示。

壳体初始形状由壳体表面dummy shell 单元确定，壳体初始形状定义如图3-41所示。

图3-40　药罩初始形状定义

图3-41　壳体初始形状定义

炸药初始形状由炸药表面dummy shell 单元确定，炸药初始形状定义如图3-42所示。

各物质的逻辑顺序，如图3-43所示。

3.3.2.6　欧拉边界条件

流场边界条件定义欧拉网格边界上流进流出网格的材料的物理性质及其位置。在MSC.Dytran 中，欧拉域的默认截断边界是对称边界条件，本项目采用1/2 模型计算，也就是说，其1/2 模型的对称面可以选用默认的边界条件。其余五个面，需要定义流出边界条件，否则会导致欧拉域内压力急剧增大。

欧拉域的边界条件如图3-44所示。

图3-42　炸药初始形状定义

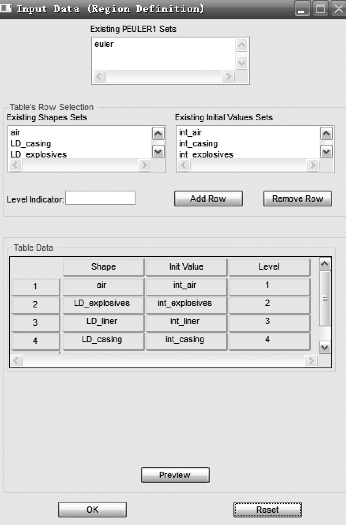
图3-43　各物质逻辑定义

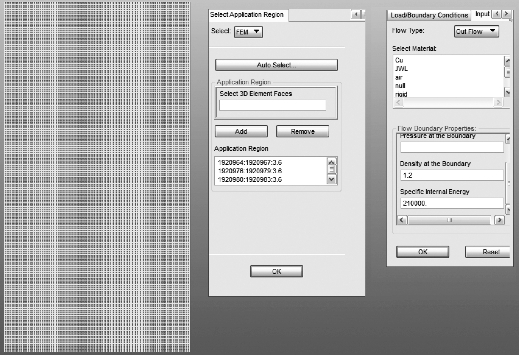
图3-44　欧拉域边界条件定义

3.3.2.7　起爆点定义

具有JWL 类型状态方程的欧拉单元在分析过程中会发生爆炸。模型中必须有一张DETSPH 卡用于起爆点的定义（图3-45）。爆炸波的波阵面是一个球形面。DETSPH 卡上定义起爆点的位置、起爆时间、爆炸波的传播速度。程序据此计算每个炸药单元的爆炸时间。不具有JWL 型状态方程的单元不受影响。

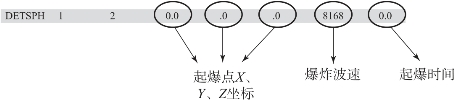
图3-45　起爆点定义

3.3.2.8　求解控制及输出控制

1.时间步长和计算结束时间控制

采用MSC.Dytran 进行有限元分析，需要定义初始时间步长和最小时间步长，以及计算结束时间。计算成形过程时间为1.5e-4s。

时间步长和计算结束时间控制如图3-46所示。

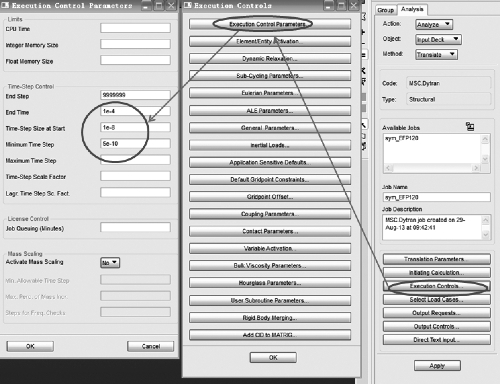
图3-46　求解控制设置

2.欧拉域内物质最大速度控制

欧拉域内物质最大速度控制如图3-47所示。

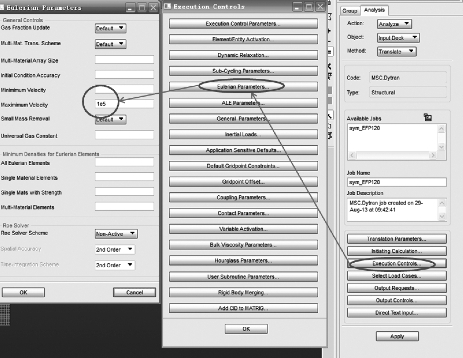
图3-47　最大速度设置

3.结果输出控制

结果输出控制，主要是方便客户定制需要的结果数据，包括动画、云图、曲线等。

结果输出控制如图3-48所示。

3.3.2.9　计算提交

在进行完前处理后，可以导出MSC.Dytran 计算文件，并打开MSC.Dytran客户端提交作业，如图3-49所示。

3.3.2.10　计算结果

计算成形过程时间为1.5e-4s，计算费时为3 374s。

计算显示，由于炸药底部中心点起爆，爆轰波以球形波的形式向外扩散，爆轰波首先轰击到药罩的底部中心点，药罩的中心首先被加速，紧跟着药罩的边缘也被加速，整个药罩被驱动沿轴向飞出，药罩在飞行过程中，由于中心先被加速，中心速度大于边缘，故药罩发生翻转，在继续飞行一段时间后，翻转完成，药罩以一种稳定的形态向前飞行。

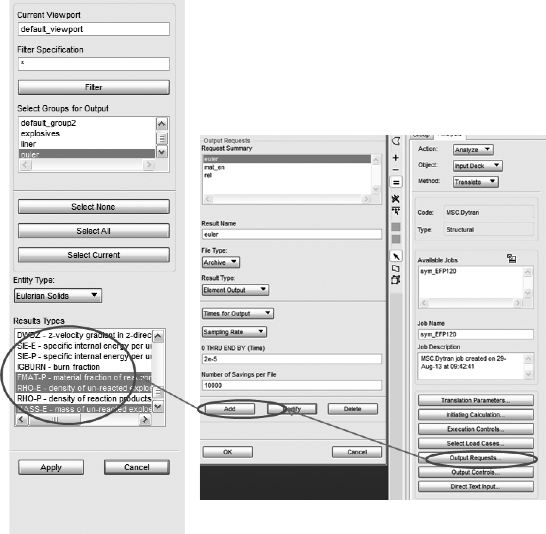
图3-48　输出控制设置

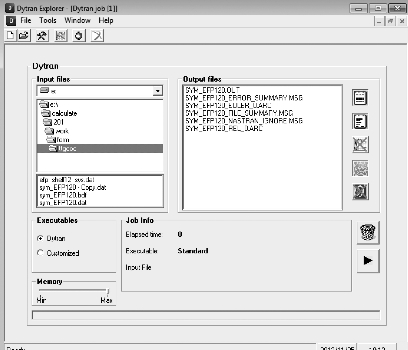
图3-49　求解提交

药罩翻转成形连续过程如图3-50所示。

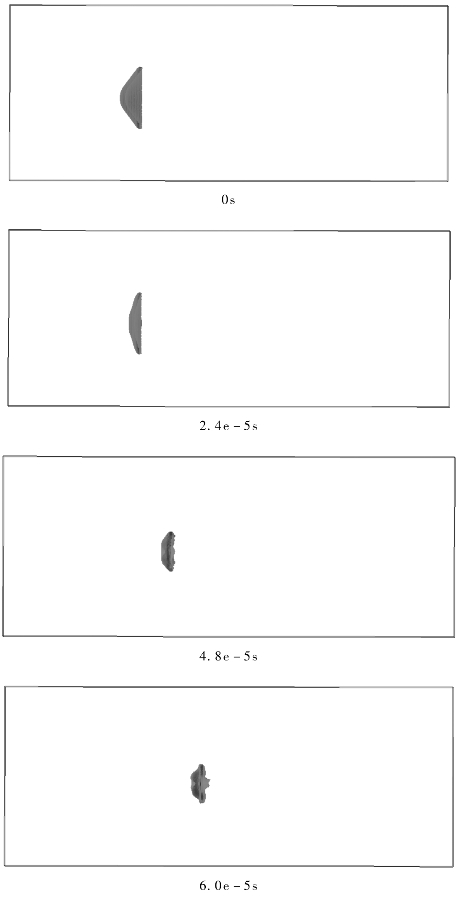
图3-50　弹丸成形过程

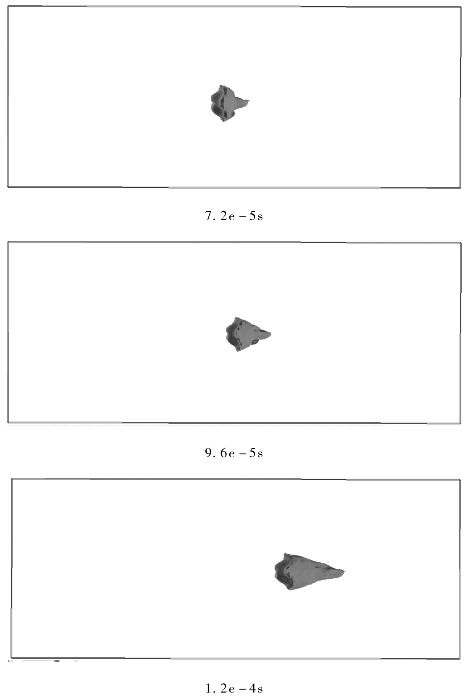
图3-50　弹丸成形过程（续）

EFP 弹丸最终成形及尺寸如图3- 51所示。

图3-51　弹丸尺寸

药罩的中心首先被加速，紧跟着药罩的边缘也被加速，整个药罩被驱动沿轴向飞出。由于EFP 弹丸采用欧拉法模拟，其弹丸翻转后的顶部物质在欧拉网格中不断运动，因此在取头部速度结果时需要先找到头部在哪个欧拉网格，然后再取出该网格的速度大小。另外，可以根据整个EFP 弹丸的动能，计算得到其平均速度曲线。

EFP 弹丸头部速度曲线和平均速度曲线如图3-52所示。

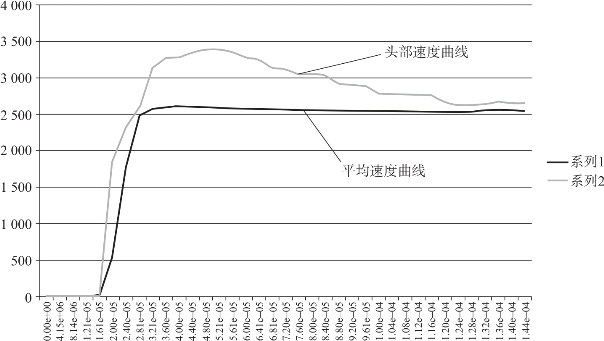
图3-52　弹丸速度时间历程曲线（见彩插）

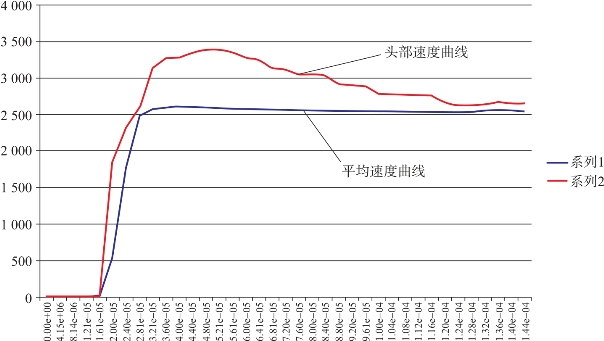
图3-52　弹丸速度时间历程曲线

3.3.2.11　小结

采用多物质欧拉法，对某型EFP 地雷装药结构进行爆炸翻转成形过程模拟仿真，成形过程清晰。爆炸开始后，爆轰波首先轰击药罩底部，底部先被加速，在3e-5s 内加速到3 450m/s 左右，然后药罩中心翻转。药罩边缘在爆轰波作用下也随即被加速，但由于药罩中心先加速，且速度高于药罩边缘，因此药罩整体被拉长，最终形成一个速度在2 520m/s 的弹丸。弹丸尺寸宽度为44mm，长度为66mm，形状为不规则锥筒形。计算EFP 弹丸头部速度和平均速度与实际及理论吻合良好。