2.4.2.1　面向控制的被控对象仿真模型开发

面向控制的被控对象模型搭建主要有两种方法：一是借助成熟的专业软件，比如AVLCruise、Advisor 或者dSPACEHIL；二是基于Matlab/Simulink 软件根据被控对象的原理建立数学模型。基于Matlab/Simulink 软件仿真是控制策略设计的重要方法，本书以串联式混合动力履带车辆为研究对象，介绍整车控制策略的仿真设计，包括驾驶员模型、发动机- 发电机组模型、动力电池组模型、车辆动力学模型、驱动电机模型等建模原理和方法，为研究混合动力履带车辆的整车控制问题提供了必要的仿真环境。建模过程中采用以经验模型为主的方法，经验值都经过实车验证，具有相对较高的精度。

1.发动机-发电机组模型

在串联式混合动力履带车辆中，发动机不直接驱动车辆，而是通过带动发电机发电，为两侧驱动电机提供电能，两侧电机驱动履带主动轮使车辆行驶。发动机和发电机之间可以通过一个变速箱来实现速度匹配。采用电压控制的发动机-发电机组模型的输入输出如图2-27所示，输入为目标转速和母线电流，输出为实际转速和可控母线电压。

图2-27　发动机-发电机组模型的输入输出

顾名思义，发动机-发电机组模型由发动机模型和发电机模型组成。由于本书主要研究控制策略的仿真，而非部件的仿真，因此只关注发动机的对外输出特性及燃油消耗特性，不关注发动机具体的燃烧过程等详细特性。因此，在发动机建模过程中，对其内部的过程可以尽可能地简化，忽略发动机的高频动态特性，建立发动机的准静态模型。发动机燃油消耗率只与发动机转速和发动机扭矩两个参数相关。根据这两个参数查万有特性表可插值得出当前的燃油消耗率，如图2-28所示。

本书中的发电机采用三相永磁同步发电机。串联式混合动力履带车辆电传动系统采取的是AC-DC-AC 形式，即发电机三相交流电经过整流后变为直流电，直流电通过逆变成三相交流电给驱动电机提供电能，因此发电机关键特征建模通常与整流桥一起采取等效电路方法来完成。永磁同步发电机及整流桥等效电路如图2-29所示。

永磁同步发电机-整流桥直流侧电压、电磁转矩方程如下：

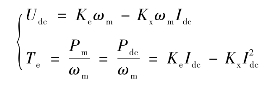
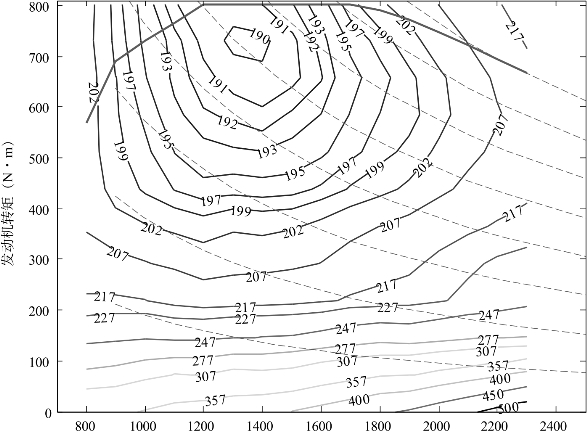
图2-28　发动机燃油经济性MAP 图

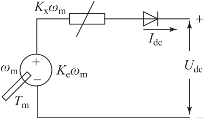
图2-29　永磁同步发电机加整流桥等效电路

式中，Te 为发电机电磁转矩；Ke 为发电机的等效电动势系数；Kx 为发电机等效阻抗系数，Kx = 3PLg/π ，其中P 为发电机极对数，Lg 为发电机电枢同步电感。

发电机输入转矩由发动机经过变速箱传递而来，速比ie-g 。根据转矩平衡有如下关系：

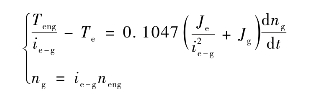
式中，Teng为发动机输出转矩；neng为发动机转速；ng 为发电机转速；Je 为发动机转动惯量；Jg 为发电机转动惯量。

从图2-30 中可以看出，发动机-发电机组建模为一个可控的电压源，向负载提供功率。

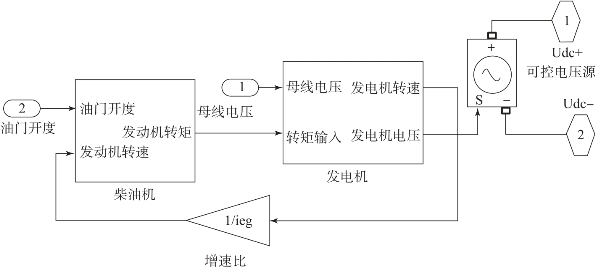
图2-30　发动机-发电机组底层模型

2.动力电池组模型

基于试验数据，建立电池组的等效电路模型，如图2-31所示。方程式表达如下：

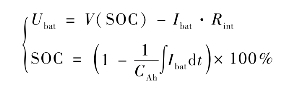
式中，Ubat为动力电池组输出电压；V（SOC）为动力电池组开路电压；Ibat为动力电池组输出电流；Rint 为动力电池内阻；CAh 为动力电池组容量；SOC 为动力电池组荷电状态。动力电池组开路电压与SOC 及内阻关系通过实验获得。

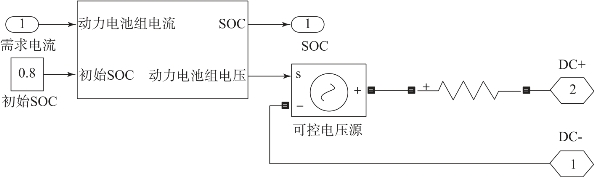
图2-31　动力电池组底层模型

3.驱动电机模型

驱动电机采用永磁同步电机，其机械输出特性曲线如图2-32所示，包括电机驱动系统的额定外特性曲线、峰值外特性曲线以及电机在不同工作点的系统效率。电机控制器接收动力学控制策略发送过来的目标转矩，控制电机转矩输出，系统模型再和当前电机允许输出的最大转矩进行比较。若目标转矩命令不大于最大转矩，则控制电机输出目标转矩值；若目标转矩超过最大转矩，则控制电机输出最大转矩值。

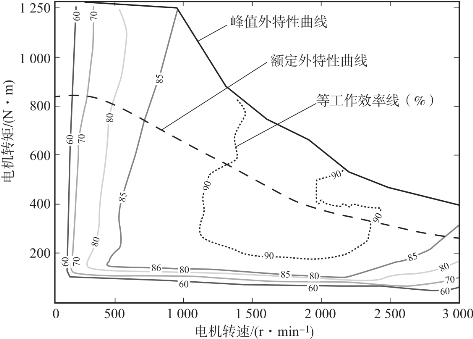
图2-32　驱动电机机械输出特性曲线

驱动电机被建模成一个可控的电流源，驱动状态时从直流母线上吸收电流，制动时回收能量反馈到回流母线，给动力电池组充电，如图2-33所示。

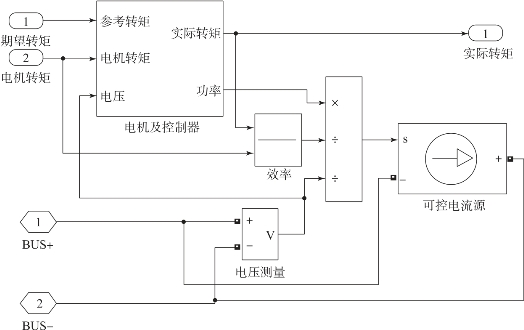
图2-33　驱动电机系统模型

4.车辆动力学模型

车辆动力学模型主要考虑纵向动力学，不考虑垂向的动态过程。通过分析履带车辆直驶和转向过程，建立如下方程组：

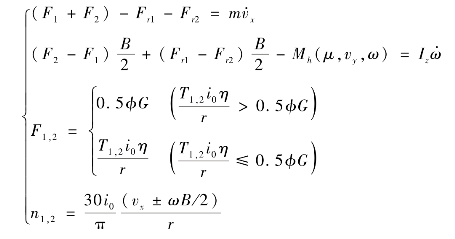
式中，F1，F2 是纵向驱动力；Fr1，Fr2 是两侧履带纵向阻力；T1，T2 是两侧驱动电机转矩；vx 为纵向车速；vy 为侧向车速；Mh 是转向阻力矩；ω 是转向角速度；Iz 为车辆z 轴方向转动惯量；m 为整车质量；φ 为滚动阻力系数；μ 为转向阻力系数，由路面状态决定；r 为主驱动轮半径；B 为两侧履带中心距；i0 为侧减速比。

根据方程组，建立如图2-34所示的履带车辆动力学模型。

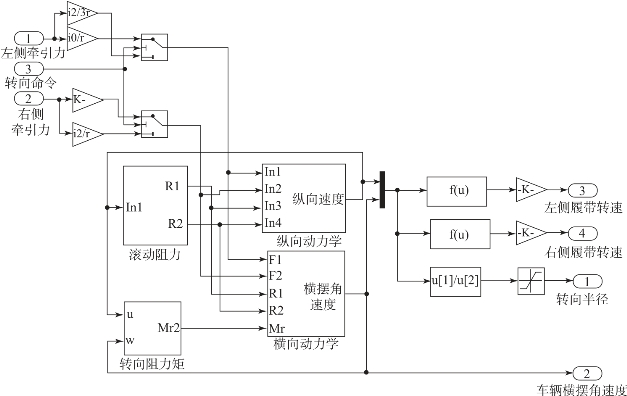
图2-34　履带车辆动力学模型

5.驾驶员模型

驾驶员模型实际上是一个车速控制器，模型中采用了一个PI 控制器，将输入的期望车速与实际车速（来自车辆动力学模型的输出反馈）的差值转变为加速踏板指令或制动踏板指令，如图2-35所示。驾驶员模型的主要变量为描述不同驾驶风格的P、I 参数。

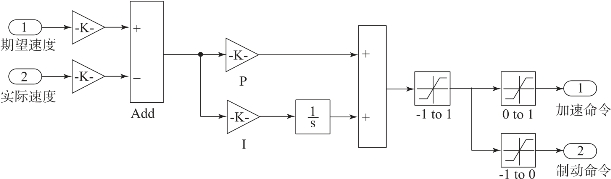
图2-35　驾驶员模型

2.4.2.2　控制系统常用理论

本书以串联式混合动力履带车辆整车控制策略开发为例，介绍常用理论方法。书中的混合动力履带车辆采用串联构型，能量源为发动机-发电机组和动力电池组，由两侧电机来驱动车辆。能量管理控制策略是混合动力车辆整车控制策略中最重要的功能。混合动力车辆能量管理控制策略的作用是在车辆的行驶过程中，在满足车辆的动力性和其他基本性能要求的前提下，根据动力总成各部件的性能特征与车辆的行驶工况，利用混合动力的节能机理，充分发挥设计方案的节能潜力，达到整车在燃油经济性和排放等方面的目标性能。

能量管理控制策略是混合动力车辆研发的核心和难点。按控制原理分类，串联混合动力车辆的能量管理控制策略可以分为恒温器模式、功率跟随模式和恒温器-功率跟随（两者混合）模式三类。恒温器模式原理：当电池荷电状态小于设置值SOCmin 时，发动机-发电机组启动并工作在最低燃油消耗点或排放点，按恒功率发电，一部分功率用来满足驱动功率需求，另一部分用来向动力电池组充电；当电池荷电状态大于设置值SOCmax 时，发动机- 发电机组关闭，由动力电池组给驱动电机提供能量，车辆工作于纯电动模式。恒温器模式优点是控制原理简单、代码容易实现和可靠性好。缺点是动力电池组功率容量要求大，对于重型车需要大量电池组，不经济也不便于布置。动力电池组经常出现大电流充放电的情况，对电池效率和寿命都不利。功率跟随模式，也叫发动机功率跟随控制策略，要求发动机的输出功率实时跟踪路面负载需求的变化，这将导致发动机频繁启停和大范围调速，影响发动机效率。恒温器-功率跟随模式；当电池荷电状态较低或负载功率较大时，发动机均会启动。当电池荷电状态高于SOCmax 或负载功率较小时，发动机关闭。当负载功率大于或小于发动机经济区域所能输出的功率时，电池组通过充放电对该功率差进行缓冲和补偿。优点是发动机一旦启动，就工作在相对经济的区域。缺点是无法获得最优的结果。

目前已经提出的能量管理控制策略按控制方法基本可以分为四类：基于规则的逻辑门限控制策略、瞬时优化控制策略、智能控制策略和全局最优控制策略。基于规则的逻辑门限控制策略原理是，根据发动机的负荷特性图，设定一组静态和动态参数来限定发动机的工作区域；同时，根据动力电池组的内阻和充放电特性，设定高效率电池荷电状态的工作区间。在此基础上，基于预先设定的判定规则来选择和切换混合动力系统的工作模式。具体控制原理可以选择恒温器控制模式或者功率跟随控制模式等。其优点是算法简单、实时性好、鲁棒性好和实用价值高；缺点是逻辑门限值的设定比较依赖工程经验和试验数据，在动态工况下对燃油经济性和排放的控制精度有待提高。瞬时优化策略采用名义油耗作为控制目标，该控制方法要求将驱动电机的能量损耗转换为等效的发动机油耗。驱动电机的等效油耗与发动机的实际油耗之和称为名义油耗。瞬时油耗模式从保证系统在每个时刻的名义油耗最小出发，动态分配不同能量源的功率。瞬时优化控制策略的缺点是需要大量的浮点运算，计算量大，不适于在线控制。智能控制策略的基本出发点是模仿人的智能，根据被控系统的定性信息和定量信息形成推理决策，以实现对难以建模的非线性复杂系统的控制。主要方法有模糊逻辑控制策略、神经网络控制策略和遗传算法控制策略。全局最优控制策略采用的一种重要方法是动态规划。动态规划理论是解决多阶段最优决策的一种数学方法，在复杂非线性系统控制优化方面应用广泛。动态规划方法的优点是可以获得全局最优的结果，缺点是计算量大且需要提前知道行驶工况，限制了实时应用。但是可以根据动态规划的结果优化现有实时控制策略，以获得较好的节能效果。

下面具体介绍几种常用的控制策略及其原理。

1.基于逻辑门限值的能量管理策略

采用发动机多点控制策略，建立发动机转速切换的规则。将发动机转速工作范围分为不同等级，每一等级覆盖一段功率范围，通过跟踪目标功率使发动机在不同转速等级上切换，从而避免发动机频繁调速。发动机转速多点控制工作原理如图2-36所示。其中（a）图为发动机工作区间（转速等级）在转速-功率平面中的分布，（b）图为发动机工作区间在其万有特性平面上的分布，A1、B1、C1 线分别与A、B、C 线相对应，Ⅰ、Ⅱ、Ⅲ表示最终划分的3个转速等级，区域kjlm、onpq 表示两个等功率转速切换区。

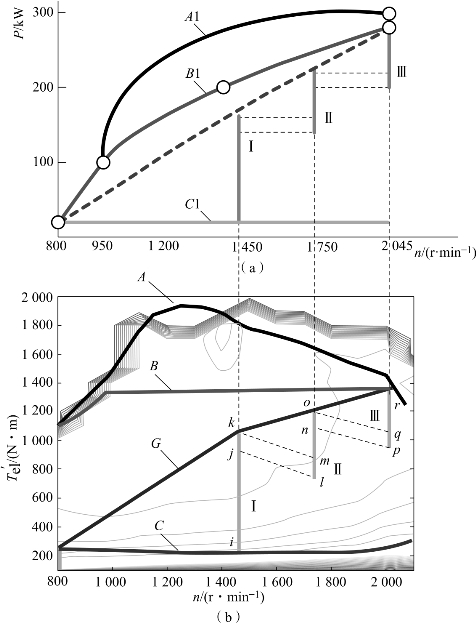
图2-36　发动机多点转速控制原理图（引自参考文献[21]）

发动机转速等级的划分如表2-2所示。

表2-2　发动机转速等级的划分

2.基于动态规划的能量管理策略

基于规则的能量管理策略控制算法简单，但是需经过大量实验才能得到合理的力矩分配曲线，且往往得不到最优结果。因此，采用动态规划算法将能量管理问题建模成一个离散的最优控制问题。首先建立下式所示混合动力履带车辆最优控制的状态方程：

x(k + 1)= f(x(k),u(k),Trqdem(k))

式中，x（k）= {SOC（k），ne（k）} 表示系统的状态向量，选为电池荷电状态SOC（k）和发动机转速ne（k）；u（k）= {acc（k），Espdcmd（k）} 表示系统的控制向量，选为发动机油门开度acc（k）和发动机转速切换命令Espdcmd（k）；Trqdem（k）为第k 时刻系统的需求扭矩，通过行驶工况计算得出。最优目标函数是寻找控制输入量使得燃油消耗最小。目标函数为整个工况油耗和工况初始及最终SOC 变化约束。目标函数表示为：

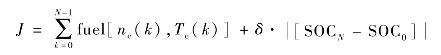(www.daowen.com)

在优化计算过程中还要对系统添加必要的约束条件，避免发动机、发电机、动力电池组工作在不合理的区域，约束不等式如下：

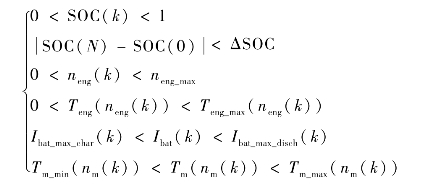
式中，neng 为发动机转速；Teng 为发动机转矩；Ibat 为电池组电流；Tm 为电机转矩。

（1）动力电池组离散状态方程。

对电池荷电状态方程求导可得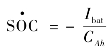，，即动力电池组的离散形式为：

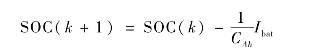
式中，。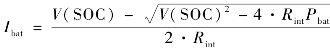

（2）发动机转速的离散方程。

对于串联混合动力车辆，发动机不受实际工况的速度约束，因此可以将它表示为与控制量相关的函数：

ne(k + 1)= ne(k)+ Espdcmd(k)

（3）动态规划算法及求解步骤。

动态规划理论的核心是最优性原理。将一个多步决策问题转化为一系列单步决策问题，然后从最后一步开始往前求解直到初始步为止。求解过程遵循以下原则，无论初始状态如何，后面的决策必须保证是一个最优的过程。

动态规划的计算步骤为：

第N-1 步：

第k 步（0 ＜k ＜N-1）：

式中，为在从第k 步开始累积的最优目标函数，即第k 步的最小燃油

消耗值。通过求解这个递归方程，直到第一步，即可求得整个工况的最小燃油消耗值。此外，还可以得到该工况下的最优控制策略u*（k）。

3.基于随机动态规划的能量管理策略

与动态规划不同，随机动态规划将驾驶员的需求功率建模成一个马尔科夫过程，能更真实地反映驾驶过程。随机动态规划优化的结果是一个全状态反馈的最优控制表格，可下载到控制器中实车应用。

双电机独立驱动的履带车辆的特点是取消了转向过程中机械滑磨损失，其功率需求通过下式计算：

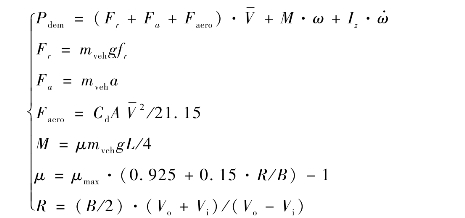
式中，Fr 是滚动阻力；Fa 是加速阻力；Faero为空气阻力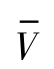；为平均车速；M 是转向阻力矩；ω 是转向角速度；Iz 为车辆垂直轴向转动惯量；mveh为整车质量；fr为滚动阻力系数；a 为直驶加速度；Cd为风阻系数；A 为迎风面积；μ 为转向阻力系数；L 为履带接地长；μmax 为转向阻力系数，由路面状态决定；R 为转向半径；B 为两侧履带中心距；Vo 和Vi 分别为外、内两侧履带速度。

车辆实际行驶中驾驶员通过操纵加速踏板或制动踏板表达功率需求，该值不可能预知，但可以把其视为随机过程，且具有马尔科夫性质，即下一时刻的需求功率只取决于当前车速和当前需求功率，而与之前的状态无关。通过统计实际的行驶工况来获得不同车速下需求功率转移概率函数。

将需求功率离散为有限个数的一列值：

平均车速同样离散为有限个数的一列值：

用转移概率Pim，j 来表示在k 时刻平均车速 和当前时刻需求功率下，k+1 时刻需求功率的概率。

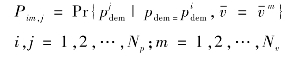
且。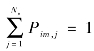

根据行驶工况求出每一时刻对应车速下的需求功率。采用最邻近法（Nearest Neighborhood）将获得的数据并量化为 。转移概率的值由最大释然估计法确定：

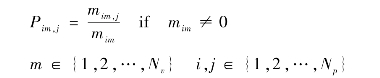
式中，mim，j 表示在车速为时，需求功率从 转移到发生的次数；mim 表示在车速为 时，需求功率总的发生转移的次数，且。

（1）马尔科夫决策问题建模。

把发动机-发电机组和电池组间功率分配看作离散时间序列马尔科夫决策问题，状态转移方程如下：

xk+1 = f(xk,uk,wk)

式中，状态量为xk = {SOC（k），neng（k）}T ；控制量取发动机电子油门开度信号，uk =thro（k）∈[0，1]；wk 为随机干扰变量，令wk = Pdem，并满足实车循环工况下的需求功率转移概率分布。

单步状态转移成本计算如下：

r(xk,uk)= Ts·F(neng(k),thro(k))+ α·(SOCk+1- SOC0)2

式中，r（xk，uk）为在xk 状态下施加控制量uk 引发的单步状态转移成本；Ts 为离散步长，取1s；F（neng（k），thro（k））代表转速neng（k）和thro（k）下的燃油消耗率，由发动机万有特性试验获得。为约束电池过度充放，在单步状态转移成本中包含下一时刻SOC 与初始SOC 的差的平方项。α 为加权因子，以调节在优化中燃油消耗与电池组能量平衡的权重。

马尔科夫决策的目的是寻找控制律π ，实现整个随机过程中的成本期望最小，表达如下：

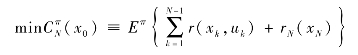
式中， 表示初始值为x0、施加控制律π 的总体成本；rN（xN）为终端成本，表达为：

rN(xN)= α·(SOCN- SOC0)2

此外系统状态或控制量受以下约束：

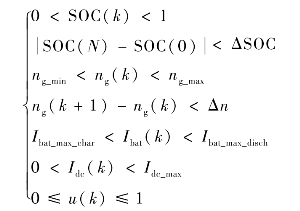
式中，ΔSOC 为允许的SOC 偏差，ng_min和ng_max分别为发电机允许最低和最高转速；Δn 为单位时间步长内允许的发电机速度增长率，Ibat_max_char 和Ibat_max_disch 为电池组最大充电电流（为负值）和放电电流，Idc_max 为发电机组最大输出电流。

（2）策略迭代法求解。

由于Pdem为随机变量，导致下一时刻状态变量被看作是条件概率，期望成本函数重新表达为：

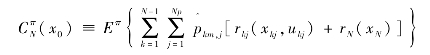
该式包括前N-1 时刻的累积成本和N 时刻的终端成本，当成为无限马尔科夫决策问题。

引入折扣因子λ 以加快收敛，总的期望成本函数表示为：

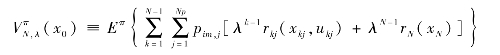
由上式得到贝尔曼最优方程的递归形式：

Cπ(xN-1)= rN-1(xN-1,uN-1)+ λ·Cπ(xN)

采用策略迭代法求解上述最优控制问题，具体算法如下：

（1）设n 为迭代次数。初始化n =0；任意假定一个初始的策略π0。

（2）策略评估。将πn 代入贝尔曼最优方程。若，则停止，取最优值函数，否则，令，继续迭代直到为止。

（3）策略改进。将第二步求得的最优值函数C* 代入迭代方程。获得针对最优值函数的控制策略，πn+1 = arg minC*。

（4）如果πn = πn+1 ，则停止。最优的策略π* = πn ；否则，n = n + 1 ，重复步骤（2）～（3）。