（1）声压与声压级

在有声波时，声场中某一点的压力与没有声波时的环境压力之差，称为声压，单位为Pa或N/m2。声压是衡量声音大小的尺度，声音越强，声压越大。

一个纯音声波的声压可用正弦波表示，即

式中　A0——声压幅值；

ω——声波圆频率；

x——到声源的距离；

c——该传声介质中的声速；

t——时间。

正常人双耳刚刚能听到的频率为1 000Hz的纯音（单一频率的声音，其瞬时声压为正弦函数）的声压是2×10－5Pa（20μPa），称为听阈声压。此值规定为声压测量的基准，记为p0。而使人耳开始产生疼痛感觉的声压，则称为痛阈声压，其值是20Pa。痛阈声压是听阈声压的106，即百万倍，可见人耳感受声压的动态范围很宽。由于声压的变化范围和人的听觉范围非常宽广，用声压值直接来衡量声音的强弱是很不方便的。为此，声学上普遍采用对数标度来度量声压，称为声压级。其定义为声压平方和听阈声压平方的比值的对数，单位为贝（B），即

由于贝尔这个单位太大，在实际使用中不方便，因此常取它的1/10即分贝为单位，则声压级

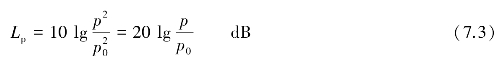
式中　Lp——声压级，dB；

p——声压，Pa；

p0——基准声压，p0＝2×10－5Pa。

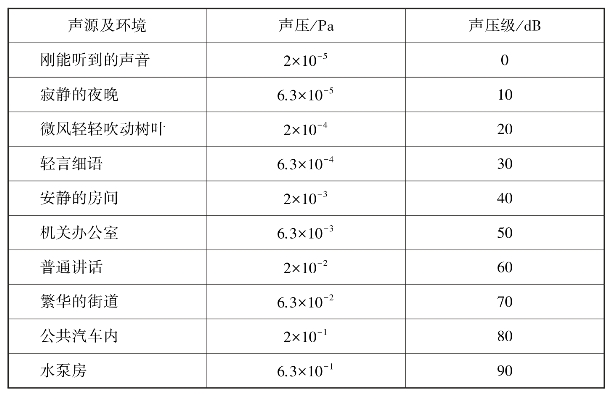
表7.2列出了一些典型声源的声压和声压级。通过这些数据，可对声压和声压级的概念有一个较为直观的了解。

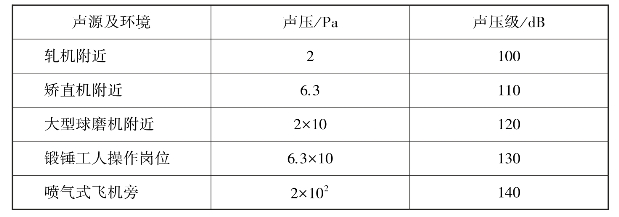
表7.2　典型声源的声压和声压级

续表

（2）声功率和声功率级

声功率是指声源在单位时间内所发出的声能，用符号W表示，单位为瓦（W），即

式中　E——声能，J；

Δt——时间，s。

声功率的基准为10－12W。由于声功率不像声压那样随离声源的距离增加而减小。因此，国际标准化组织（ISO）推荐测试噪声源的声功率。

以10－12W为基准声功率W0，声功率级定义为

声功率级的大小可通过对声压级的测量值计算得到。

（3）声强和声强级

声强是指单位面积上的声功率，即

式中　I——声强，W/m2；

S——声传播面积，m2。

声强与声压幅值的平方成反比，因此，它和声压一样也是随离开声源的距离增大而减小。此外，声强与传声介质的性质有关。例如，在空气中和水中相同频率相同速度幅值的声波，水中的声强要比空气中的声强约大3 600倍。

声强级是以1 000Hz纯音的听阈声强值10－12W/m2为基准定义的，即

式中　LI——声强级，dB；

I——声强，W/m2；

I0——听阈声强，I0＝10－12W/m2。

声强级和声压级之间的关系为

式中　ρ——传声介质的密度，kg/m3；

c——传声介质的声速，m/s。

（4）声压级的合成

当两个纯音同时发生时，其合成效应取决于接收器处的声压幅值、频率和相位关系。若空间中某一点有两个声波。其声压分别为

(www.daowen.com)

式中　p1，p2——声波1和2的瞬时声压；

A1，A2——声波1和2的声压幅值；

ω1，ω2——声波1和2的圆频率；

φ1，φ2——声波1和2的相位。

这两个声波产生的瞬时声压为它们瞬时声压之和，则合成后声压的均方值为

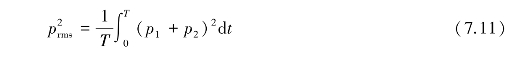
式中　T——平均时间。T≫1/fmin，fmin为声波的最小频率。

将式（7.9）和式（7.10）代入式（7.11），得

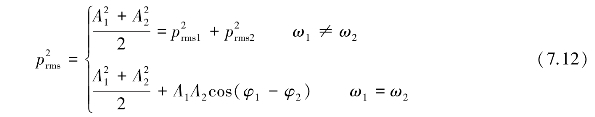
式中　——声波1和2的均方声压。

当两个纯音的振幅和频率相等，相位差为零时，即A2＝A1，ω2＝ω1，φ2＝φ1，其合成声波的均方声压为

则两个声波的合成声压级相对于单个纯音的声压级的增加量为

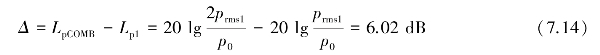
式中　LpCOMB——两个声波的合成声压级；

Lp1——声波1的声压级。

由式（7.12）的第一个表达式可得出两个声压幅值相同，但频率不同的纯音合成后的合成声压级与单个纯音声压级之差为

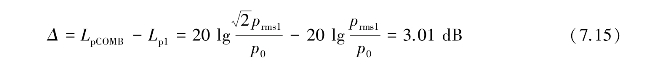
当声场中有两个或两个以上的声源存在时，任何一点的声压是所有声源共同作用的结果。当用声压级表示噪声时，且不考虑各声源发出声波之间的相干情况，则合成总声压级Lpt可表示为

式中　Lpt——合成声压级；

Lpi——第i个声源单独存在时的声压级。

例7.1　已知某声场中存在两个声源，其单独存在时的声压级分别为80dB和90dB，试求总声压级。

解　由式（7.16）可得

Lpt＝10lg（1080/10＋1090/10）＝90.41dB

多个声波合成时分贝的增值也可利用表7.3近似求取，采用表7.3时可采用两两合成的方法求取，合成结果与合成次序无关。

表7.3　分贝增值表/dB

注：Lp1＞Lp2。

以例7.1为例，采用分贝增值表可这样计算总声压级。两声源的声压级相差10dB，查表7.3可知，分贝增量为0.4dB，所以总声压级为90dB＋0.4dB＝90.4dB。查表所得结果与计算结果仅0.01dB的误差，在工程上是可以接受的。

当在现场进行噪声测试时，为了排除环境噪声（本底噪声、背景噪声）的影响，得到声源声压级的实际大小，需要从测量结果中扣除环境噪声的影响，则可采用下式计算声源的声压级，即

式中　Lpso——所求声源的声压级，dB；

Lpt——总声压级，dB；

Lpe——环境声压级，dB。

例7.2　在某厂房某点测得机器停止运转时环境噪声的声压级为80dB，机器运转时的声压级为88dB，求该机器在该点产生的声压级。

解　由式（7.17）可得

Lpso＝10 lg（1088/10－1080/10）dB＝87.25dB

分贝扣除也可采用表7.4的环境噪声扣除表进行近似计算。

表7.4　环境噪声扣除值表/dB

例7.2也可采用表7.4计算机器产生的声压级。总声压级与环境声压级相差8dB，查表7.4得，应该从总声压级中扣除0.73dB，即该机器产生的声压级为88dB－0.73dB＝87.27dB。对比用式（7.17）的计算结果，存在误差0.02dB。

当总噪声和环境噪声相等时，其声压级差值为3dB。如果总噪声与环境噪声的声压级差值小于3dB，测量结果无效，因为此时环境声压级比被测声源的真实声压级还高。如果碰到级差小于3dB的情况时，可采用式（7.17）计算。当总噪声与环境噪声之差大于10dB时，环境噪声对测量结果的影响可以忽略不计，所测得的总声压级可认为就是声源的实际声压级。

声压级的叠加和扣除还可采用如图7.1所示的分贝增值图和如图7.2所示的环境噪声影响修正曲线来进行计算。

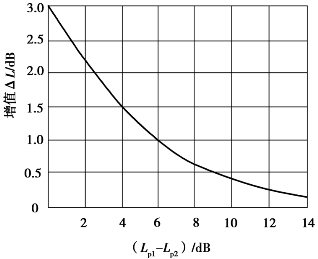
图7.1　分贝增值图

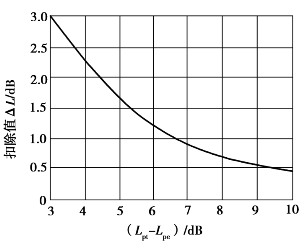
图7.2　环境噪声影响修正曲线