（1）拉（压）的测量

例6.1　测量如图6.5所示构件的拉应变，要考虑温度效应。

图6.5　受拉试件

解　方法1：按如图6.6（a）所示的贴应变片，如图6.6（b）所示的接桥。其中，R1为工作片，R2为补偿片。

工作片R1的应变为ε1＝εP＋εT，其中，εP为拉力引起的应变，εT为温度变化引起的应变；补偿片R2的应变为ε2＝εT。最终电桥的输出电压为

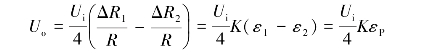
方法2：按如图6.7（a）所示的贴片，如图6.7（b）所示的接桥，R1和R2都为工作片。

R1的应变为ε1＝εP＋εT，R2的应变为ε2＝－μεP＋εT。其中，μ为被测试件的泊松比。最终电桥的输出电压为

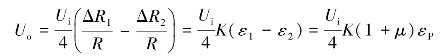
图6.6　圆轴件拉应变测量方法1

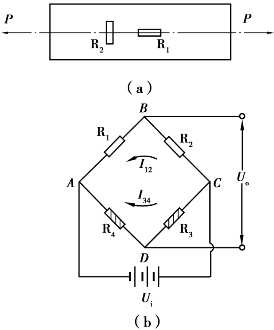
图6.7　圆轴件拉应变测量方法2

（2）弯矩测量

例6.2　测量如图6.8所示的试件所受到的弯矩，要考虑温度效应。

图6.8　测量弯矩

解　方法1：按如图6.9（a）所示贴应变片，按如图6.9（b）所示的接桥。其中，R1为工作片，R2为补偿片。

工作片R1的应变为ε1＝εM＋εT。其中，εM为弯矩引起的应变，εT为温度变化引起的应变；补偿片R2的应变为ε2＝εT。因此，最终电桥的输出电压为

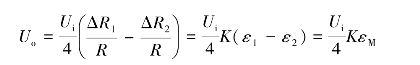
方法2：按如图6.10（a）所示的贴片，如图6.10（b）所示的接桥，R1和R2都为工作片。

R1的应变ε1＝εM＋εT，R2的应变ε2＝－εM＋εT。因此，最终电桥的输出电压为

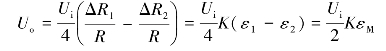
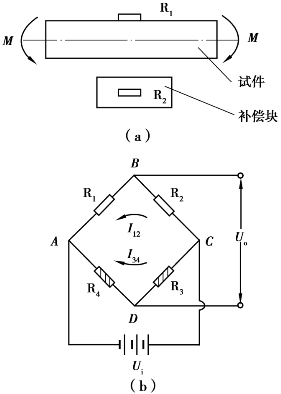
图6.9　圆轴件弯矩测量方法1

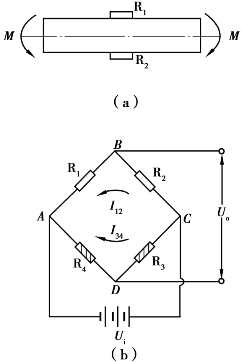
图6.10　圆轴件弯矩测量方法2

（3）拉弯联合作用下弯矩或拉力的测量

杆件在拉力P和弯矩M联合作用下的变形如果在弹性范围内可用叠加原理求出总的变形，即联合作用下的变形可看成P和M单独作用下杆件变形的叠加。

例6.3　如图6.11所示的试件受拉力和弯矩共同作用，试测量弯矩引起的应变而排除拉力。

图6.11　受拉力和弯矩共同作用的试件(www.daowen.com)

解　采用如图6.10所示的贴片和接桥方式，应变片R1的应变为ε1＝εP＋εM＋εT，应变片R2的应变为ε2＝εP－εM＋εT。因此，电桥总的电压输出为

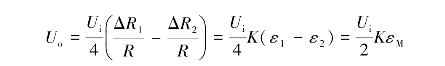
例6.4　如图6.11所示的试件受拉力和弯矩共同作用，试测量拉力引起的应变而排除弯矩。

解　方法1：按如图6.12（a）所示贴应变片，按如图6.12（b）所示的接桥。其中，R1，R3为工作片；R2，R4为补偿片。

工作片R1的应变为ε1＝εP＋εM＋εT，补偿片R2的应变为ε2＝εT，工作片R3的应变为ε3＝εP－εM＋εT，补偿片R4的应变为ε4＝εT。因此，电桥总的电压输出为

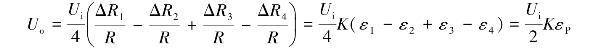
方法2：贴片方式如图6.13所示，接桥方式如图6.12（b）所示。其中，R1，R2，R3，R4均为工作片。

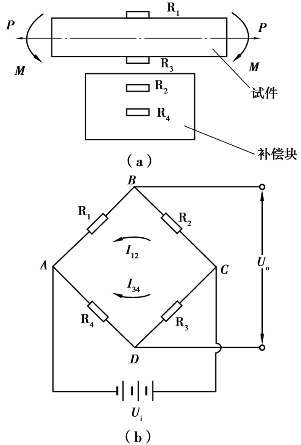
图6.12　排除弯矩测拉力方法1

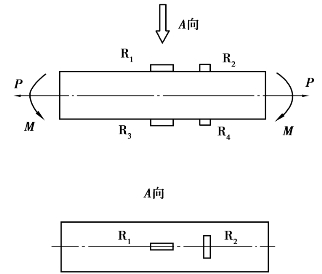
图6.13　排除弯矩测拉力方法2

应变片R1的应变为ε1＝εP＋εM＋εT，应变片R2的应变为ε2＝－μεP－μεM＋εT，应变片R3的应变为ε3＝εP－εM＋εT，应变片R4的应变为ε4＝－μεP＋μεM＋εT。因此，电桥总的电压输出为

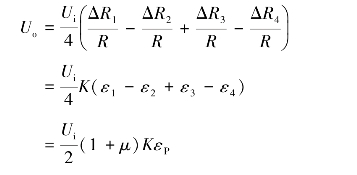
（4）扭矩的测量

例6.5　测量如图6.14所示的圆轴在纯扭矩作用下的应变。

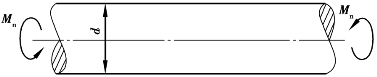
图6.14　受扭矩作用的圆轴试件

解　对于受纯扭矩的圆轴，其切应力为

式中　Mn——扭矩；

d——圆轴直径。

主应力方向与轴线成45°，且

式中　σ1，σ2——主应力。

由广义胡克定律可知，该点的主应变为

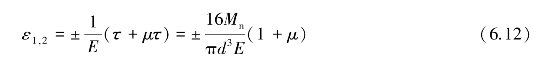
式中　E——圆轴试件的弹性模量；

μ——圆轴试件的泊松比。

由式（6.12）可知，只要测出主应变ε1或ε2，就可以求出扭矩Mn。

在与轴线成45°角的方向上分别粘贴两片应变片，如图6.15（a）所示。接桥方式如图6.15（b）所示。应变片R1的应变为ε1＝ε＋εT，应变片R2的应变为ε2＝－ε＋εT。因此，则总的电压输出为

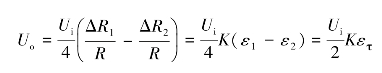
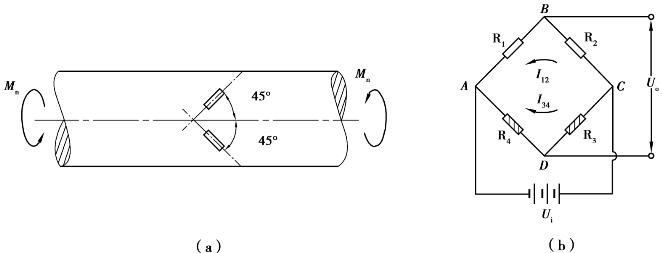
图6.15　扭矩的测量