在对实际的工程结构进行振动分析时，常将它进行简化，单自由度系统是最简化的形式。单自由度系统是指在任意时刻只用一个广义坐标即可完全确定其位置的系统，是最基本的振动模型。它一般可由一个质量块、一个弹簧和一个黏性阻尼器组成。其结构如图5.1所示。

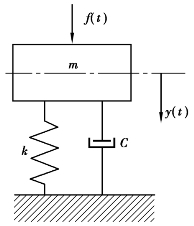
图5.1　单自由度系统在力作用下的受迫振动模型

如图5.1所示的单自由度系统，假设作用在质量块上的力为f（t），质量块的位移为y（t），则其受迫振动的运动方程为

式中　m——质量块质量；

C——阻尼器阻尼系数；

k——弹簧刚度系数。

当f（t）为正弦激励，即f（t）＝F0sin ωt时，系统稳态时的频率响应函数为

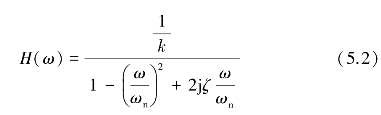
其幅频特性和相频特性分别为

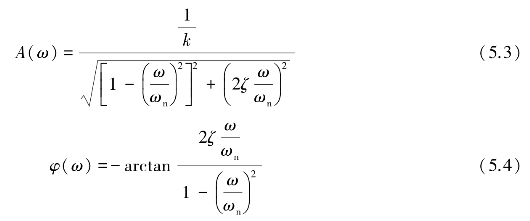(www.daowen.com)

式中　ωn——系统的固有频率，；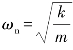

ζ——系统的阻尼比，。

根据式（5.3）和式（5.4）可作出系统的幅频特性曲线和相频特性曲线，如图5.2所示。

从幅频特性曲线和相频特性曲线可得出以下一些结论：

①当ω＝0时，A（ω）＝1/k，φ（ω）＝0，即单位静力使质量块m发生静位移1/k。

②当ω≪ωn时，A（ω）变化平缓，与静态激振力引起的位移接近，φ（ω）＜－90°。

③幅频特性曲线上幅值最大处的频率ωm，称为谐振频率。谐振频率，此时的谐振振幅为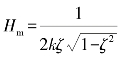；当阻尼增加时，谐振峰向原点移动，谐振振幅显著减小，当ζ＞0.707时，系统不出现谐振峰。

④ω＝ωn时，无论ζ为何值，φ（ω）＝－90°，此时称为相位共振。对于小阻尼系统，在ω＝ωn附近，相频特性曲线陡峭，故用相频特性曲线来测定固有频率比较准确。

⑤当ω≫ωn时，A（ω）→0，φ（ω）→－180°，即系统的振动位移和激励力反相。常利用这一区域指导减振设计。

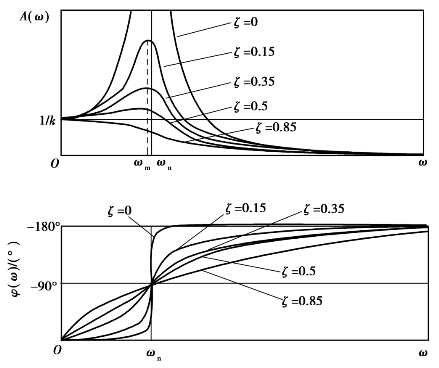
图5.2　单自由度系统受到力作用的幅频特性和相频特性曲线