数字信号处理先要把一个时间上连续的模拟信号转换为计算机能接收处理的数字信号，模拟信号数字化的过程包含截断、采样和量化等步骤。

（1）截断与泄露

计算机只能处理有限长的信号，因此，必须将过长的时间信号加以截断，即将信号乘以一个有限宽的矩形窗函数。下面以对余弦函数x（t）＝cos 2πf0t加矩形窗wT（t）为例说明加窗后信号的变化，如图4.19所示。

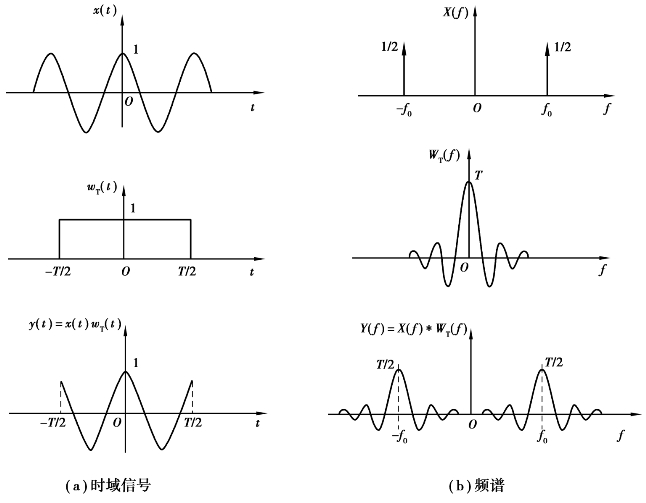
图4.19　余弦信号被矩形窗函数截断的时域信号及频谱

设窗函数

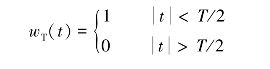
则加窗后的信号

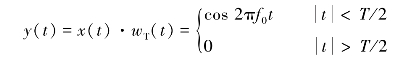
由于加窗后窗外的数据全部置零，波形发生畸变，其频谱也会发生变化，这就会产生截断误差。

加窗前，x（t）＝cos 2πf0t的频谱为

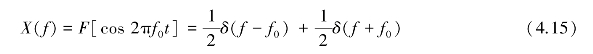
其频谱图如图4.19（b）所示。

加窗后，y（t）的频谱为

即加窗后，余弦信号的频谱相当于其原频谱与矩形窗函数的卷积，其结果是将矩形窗函数的频谱乘以1/2后分别搬移到±f0处，如图4.19所示。

由图4.19可知，原余弦信号的能量仅存在于±f0处，被截断后，在±f0两侧都出现了频率分量，即截断后，信号的能量扩散到了理论上的无穷宽频带中去，这种现象被称为泄露。增加窗函数的长度T，矩形窗函数的主瓣宽度将变窄，截断信号的泄露误差将减小。

由于截断后信号的带宽变宽，因此，无论采样频率多高，信号总是会出现混叠，也就是截断必然会导致一些误差。为了减小泄露，应该选择合适的窗函数。一个理想的窗函数主瓣宽度要小，即带宽要窄，旁瓣高度与主瓣高度相比要小，且衰减要快。

（2）采样与频率混叠(www.daowen.com)

采样是用一个等时距的周期脉冲序列s（t）（采样函数）去乘以连续时间信号x（t），时距Ts为采样间隔，则采样频率

由频域卷积定理可知，采样后信号的频谱为

采样函数s（t）及其频谱S（f）如图4.20（a）、（b）所示。假设x（t）的时域波形及其频谱X（f）如图4.20（c）、（d）所示，则采样后的时间信号及其频谱则如图4.20（e）、（f）所示。将采样后信号频谱通过低通滤波器，则可恢复出x（t）的频谱X（f）。

采样时，如果采样时间间隔Ts较大，即采样频率fs较小，当fs＜2fm，fm为连续时间信号频谱的最高频率成分，则可能出现频率混叠，如图4.21所示。发生频率混叠后，采样后信号的频谱通过低通滤波器后不能完整地恢复出原时间信号的频谱。即在对一个有限带宽的时间信号x（t）采样时，为了保证采样后的信号能不失真地还原出原信号，则采样频率fs应该大于等于信号中最高频率成分fm的2倍，这也即是时域采样定理。

图4.20　采样过程及采样后信号频谱

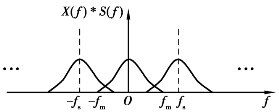
图4.21　频率混叠现象

为了避免和减小频率混叠误差，可以采取以下两个方法：

①采用尽可能高的采样频率，但是采样频率过高，在模拟信号长度一定的情况下，会导致采样数据点数增加，数值计算工作量增大；如果采样数据点数一定，又会使样本长度减小，导致信号数字谱分析的频率分辨力下降。

②在离散采样前对被分析的模拟信号进行有限带宽处理，即用低通滤波器对模拟信号进行预处理，滤除高频成分和干扰，使信号带宽限制在一定的范围内，这也被称为抗频混滤波。由于信号经过抗频混滤波后，信号中的最高频率已经确定，则可根据采样定理合理地选择采样频率。由于实际使用的抗频混低通滤波器不具有理想的截止特性，阻带内的频率分量只是受到极大的衰减而并没有被完全滤除，因此，一般采样频率为抗频混低通滤波器名义上截止频率的2.5～4倍。

（3）量化和量化误差

量化是将采样所得的离散信号的电压幅值用二进制数码组表示，使离散信号变成数字信号的过程。量化需要从一组有限个离散电平中取一个来近似代表采样点的信号实际幅值电平，这些离散电平称为量化电平，每个量化电平对应一个二进制数码。

A/D转换器的位数是一定的，一个b位的二进制数，共有L＝2b个数码。如果A/D转换器允许的动态工作范围为D（如±5V或0～10V），则两相邻量化电平之间的差Δx为

当离散信号采样值x（n）的电平落在两个相邻量化电平之间时，就要舍入相近的一个量化电平上。该量化电平与信号实际电平之间的差值称为量化误差ε（n）。量化误差的最大值为1/Δx，均值为零，其均方值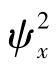为Δx2/12，误差的标准差σx为0.29Δx。实际上，与信号获取、处±（Δx/2），可认为量化误差在（－Δx/2，＋Δx/2）区间各点出现的概率是相等的，其概率密度为理的其他误差相比，量化误差通常不算大。