RC滤波器是测试系统中常用的一类滤波器。RC滤波器分为无源滤波器和有源滤波器。由于RC滤波器低频特性较好，故多用于频率相对不高的信号处理和分析。

（1）RC无源滤波器

RC无源滤波器不需要电源，电路简单，抗干扰能力强，选用标准阻容元件即可实现。

1）RC低通滤波器

RC低通滤波器的典型电路和幅频特性如图4.12所示。设电路的输入信号为ur（t），输出信号为uc（t），该滤波器为一阶系统，其时间常数为＝RC，则其频率响应函数为

幅频特性为

图4.12　RC低通滤波器典型电路和幅频特性

由幅频特性可知，当输入信号的频率ω≪1/时，A（ω）为常数，信号不衰减；当ω＝1/时，A（ω）＝A0，信号衰减3dB。由此可知，ωc2＝1/即为低通滤波器的上截止频率。由于1/＝1/RC，因此，通过适当改变RC参数，可改变滤波器的截止频率。

2）RC高通滤波器

RC高通滤波器的典型电路和幅频特性如图4.13所示。该电路为一阶系统，其时间常数为＝RC，则其频率响应函数为

幅频特性为

图4.13　RC高通滤波器典型电路和幅频特性

由图4.13（b）可知，当输入信号频率ω≫1/时，信号几乎不衰减；当ω＝1/时，A（ω）＝A0，信号衰减3dB，ωc1＝1/即为高通滤波器的下截止频率。

3）RC带通滤波器

当ωc2＞ωc1时，将RC低通滤波器和高通滤波器串联起来，即可组成RC带通滤波器，如图4.14（a）所示。由于两个串联环节之间存在负载效应，会削弱信号和改变整个系统的频率响应特性。因此，通常在两个环节之间串入具有高输入阻抗的放大器进行隔离，如图4.14（b）所示。这样的RC带通滤波器为有源滤波器，其频率响应函数为3个环节的串联，即

式中(www.daowen.com)

带通滤波器的上截止频率ωc2＝1/2，下截止频率ωc1＝1/1。

图4.14　RC带通滤波器

图4.15　RC带阻滤波器

4）RC带阻滤波器

当高通滤波器的下截止频率高于低通滤波器的上截止频率，即ωc1＞ωc2时，将高通滤波器和低通滤波器并联起来就构成了RC带阻滤波器，如图4.15所示。

（2）RC有源滤波器

RC无源滤波器仅由电阻和电容元件构成，都是低阶系统，过渡带衰减缓慢，选择性差。将几个RC无源滤波器串联起来就可提高阶次，但级间耦合的负载效应会使信号逐级减弱，采用有源滤波器则可克服这些缺点，如图4.14（b）所示。

RC有源滤波器是用RC无源网络和运算放大器等有源器件组合在一起构成的，它除了可放大信号之外，具有高输入阻抗的运算放大器还可进行级间隔离，清除或减小负载效应的影响。因此，有源滤波器往往可多级串联组成高阶滤波器，提高滤波器的选择性。

1）一阶RC有源低通滤波器

如图4.16（a）所示，将简单一阶RC低通滤波器的输出端接到运算放大器的同相输入端，则可构成一个基本的一阶有源低通滤波器，运算放大器起到隔离负载影响、提高增益和提高负载的作用。该滤波器的放大倍数为

如果把RC高通网络作为运算放大器的（见图4.16（b）），也可得到低通滤波器的作用。其放大倍数为

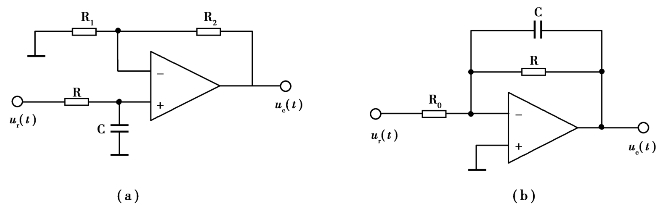
图4.16　一阶有源低通滤波器

2）二阶RC有源低通滤波器

提高滤波器的阶次可改善滤波器的选择性、增大通频带以外信号的衰减量，将两种一阶低通滤波器组成起来可构成二阶有源低通滤波器，如图4.17所示。其中，图4.17（b）是一种改进后的电路，这种电路由于形成了多路负反馈削弱RF在调谐频率附近的负反馈作用，滤波器的特性更接近理想低通滤波器，滤波器特性更好一些。

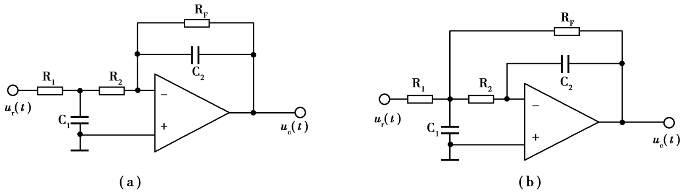
图4.17　二阶有源低通滤波器

高阶滤波器可用一阶和二阶滤波器作为基本单元，级联而成。滤波器串联得越多，阶次越高，其幅频特性越接近理想特性，但相频特性的非线性会增加。