通常情况下测试系统动态特性的测定，是通过试验的方法实现的，最常用的方法有频率响应法、阶跃响应法和脉冲响应法。这里，主要介绍频率响应法、阶跃响应法。如前所述，一阶系统的主要动态特性参数是时间常数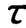，而二阶系统的主要动态特性参数是固有频率ωn和阻尼比ζ。对测试系统的动态特性参数的测定，是测试系统可靠性和准确度保证的前提。一方面新的测试系统的动态特性参数，除了理论计算外，必须通过试验验证以最终确定；另一方面任何测试系统的动态特性都会发生变化，为了确保测试的可靠性，也应该定期或在测试之前校准测试系统。另外，对于未知特性的系统，有必要通过试验了解系统的动态特性。

（1）频率响应法

如图2.15所示为系统动态特性测定试验原理框图。通过稳态正弦激励试验可求得测试系统的动态特性。具体做法如下：测试时，给测试系统输入正弦信号x（t）＝X0sin 2πft，刚开始时正弦输入信号的频率f从接近零频的足够低的频率开始，在输出达到稳定后测量输出信号和输入信号的幅值比和相位差，即可得到在该频率f下测试系统的传输特性。然后逐渐增加正弦信号的频率，并测出每一个频率对应的输出信号和输入信号的幅值比和相位差，直到输出信号的幅值减少到初始输出幅值一半止，则可得到测试系统的幅频特性曲线A（f）和相频特性曲线φ（f）。

图2.15　系统特性识别试验原理框图

对于一阶系统，利用系统幅频特性与相频特性的关系，可直接由频率响应试验得到系统的幅频特性曲线和相频特性曲线并确定系统的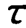值。当一阶系统的A（ω）为0.707时，对应的1/ω＝即为所求，如图2.10所示。理想的一阶系统的波德图中输出与输入的幅值比曲线在低频段为水平直线，在高频段则趋近于斜率为－20dB/10倍频的倾斜直线，转折频率点所对应的A（ω）即为0.707。据此，也可由试验曲线形状偏离理想曲线的程度判断被测系统是否属于一阶系统。

对于二阶系统，理论上根据试验得到的相频特性曲线，就可直接估计其动态特性参数ωn和ζ，因为输出相角滞后于输入相位角90°时，频率比ω/ωn＝1，即ω＝ωn时特性曲线上对应点的斜率为阻尼比ζ。但是，该点曲线陡峭，准确的相角测试比较困难。因此，通常利用幅频特性曲线来估计系统的动态特性参数：对于ζ＜1的欠阻尼二阶系统，其幅频特性曲线的峰值处于稍微偏离ωn的ωr处（见图2.11），两者之间的关系式为

欠阻尼二阶系统固有频率ωr处的输出和0频率输出处的幅频特性比为

由式（2.46）和式（2.47）可解出ωn和ζ。

另外，ζ的估计常采用以下方法，由试验得到的幅频特性曲线，曲线上峰值对应的频率为ωn，如图2.16所示。在峰值的1/处，作一水平线交幅频特性曲线于a、b两点，其对应的频率为ω1，ω2，则阻尼比的估计值为

此法称为半功率点法。

（2）阶跃响应法

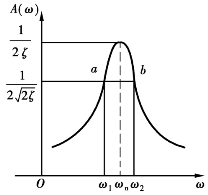
图2.16　二阶系统的阻尼比估计

阶跃响应法是给被测系统输入一阶跃信号，再根据所测得的阶跃响应曲线求取一阶测试系统的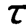以及二阶测试系统的ωn和ζ的一种试验方法。测试时，应根据测试系统可能的最大超调量来选择阶跃输入信号的幅值，当测试系统的超调量较大时，应选择较小的阶跃输入信号幅值。

1）一阶系统特性参数的阶跃响应确定法

根据一阶系统的单位阶跃响应的特点，在t＝时，y（t）＝0.632。因此，确定一阶系统时间常数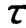的最简单的方法是在输入阶跃信号后测其阶跃响应（见图2.17（a））。当输出值达到稳态值的63.2％时所需的时间即为系统的时间常数。但是，如此求取的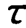值，由于没有事先检验被测系统是否是一阶系统，测试仅仅依赖于起点和终点两个瞬时值而没有涉及阶跃响应的全过程，加之起始时间t＝0点不易确定，因此，这种方法的可靠性和精确度不高。

图2.17　一阶系统的阶跃响应试验

下面介绍另一种确定一阶系统时间常数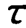的方法：一阶系统的阶跃响应函数为

如果被测系统是一阶系统，其阶跃响应必将满足该方程。因此，如果构造线性的函数为

则对于一个一阶系统，存在关系

1－yu（t）＝eZ

两边取对数，即有

由ln［1－yu（t）］确定Z和时间t之间应呈线性关系，也就是说当加载阶跃输入一阶系统后，沿时间历程记录不同时刻的yu（t），若在Z⁃t直角坐标系绘出Z与t的关系图，应该是一条直线；反之，如果得不到直线关系Z与t的关系图，则被测系统将不属于一阶系统。由此，对于满足线性关系的被测系统，可根据Z与t的关系图（见图2.17（b）），确定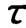值为

这种方法反映了阶跃响应的全过程，如果所测得的各数据点在Z⁃t直角坐标系中的分布近似地在一条直线上，将确信该系统为一阶系统。由于采用的直线可以是接近各数据点的最佳的拟合直线，故得到的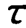值有较高的精度。

2）二阶系统特性参数的阶跃响应确定法

二阶系统的阻尼比，通常取值范围在ζ＝0.6～0.8，由于静态灵敏度系数S可通过静态标定确定，此处为便于分析，取灵敏度系数S＝1，这种典型的欠阻尼二阶系统的阶跃响应函数为

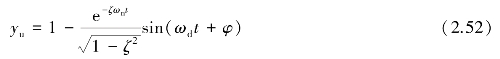(www.daowen.com)

式中

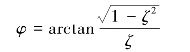
二阶系统的阶跃响应如图2.18所示，是以为圆频率且以指数规律衰减振荡波形，ωd称为有阻尼固有频率，可由阶跃响应试验记录的波形图算出。

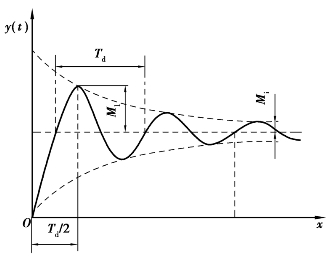
图2.18　欠阻尼二阶系统的阶跃响应

定义最大超调量

分析阶跃响应曲线可知，曲线的极值发生在t＝tp＝0，π/ωd，2π/ωd，…，处；最大超调量出现在tp＝Td/2＝π/ωd处。

将tp、式（2.52）以及yu（∞）＝1代入式（2.53），可求得最大超调量Mp和阻尼比之间的关系为

即

如果测得的阶跃响应是较长的瞬变过程，即记录的阶跃响应曲线有若干个超调量出现时，则可利用任意两个超调量Mi和Mi＋n来求取被测系统的阻尼比。

设相隔周期数为n的任意两个超调量Mi和Mi＋n，其对应的时间分别是ti和ti＋n，则

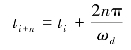
注意到二阶系统阶跃响应的任一波峰所对应的超调量Mi为

所以

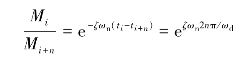
令

则化简整理可得

由此可得

根据式（2.57）和式（2.59），即可求得ζ。

（3）脉冲响应法

脉冲响应法是给被测系统施以脉冲激励，然后通过测量时域脉冲响应，根据响应特征，确定系统的特征参数，或者通过计算输入输出的互谱和输入的自谱，由H（f）＝Gxy（f）/Gx（f）得到系统的频率响应函数。

分析可知，对于一个静态灵敏度为S的一阶系统，当t＝0＋时，其脉冲响应函数的值为式中，A为脉冲的面积，因此，由测得的0＋时脉冲响应值即可确定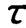。实测时，理想的脉冲输入无法获得，但只要脉冲作用时间足够小，通常要求小于0.1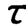，而对脉冲波形可不予限制，则确定的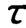有足够的精度。

对于小阻尼二阶系统，任何快速的瞬态输入所产生的响应将是幅值呈指数衰减正弦波，设相隔周期数为n的任意两个波峰值为Mi和Mi＋n，则系统的ζ可近似求得

如图2.19所示为脉冲激励试验原理框图。被测系统是机械系统，用脉冲锤敲击被测对象，给系统以脉冲输入，输出的振动信号由加速度计检出，然后通过对输入、输出信号的频谱分析，得到系统的频率响应函数。由于脉冲输入信号具有很宽频带，因此，识别的频带宽度宽，有很高的识别效率。

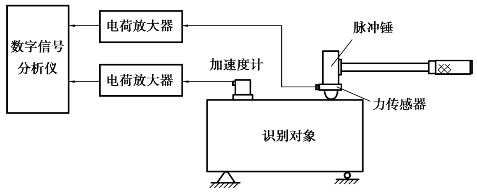
图2.19　脉冲激振试验原理框图