测试系统动态传递特性的时域描述,指的是用时域函数或时域特征参数来描述测试系统的输出量与变化的输入量之间的内在联系。通常是以一些典型信号如脉冲信号、阶跃信号、斜坡信号及正弦信号等作为输入,加载到测试系统,以特定输入下的时域响应的特征参数如响应速度、峰值时间、稳态输出及超调量等来描述系统的动态传递特性。
(1)单位脉冲输入下系统的脉冲响应函数
若输入信号为单位脉冲信号x(t)=δ(t),根据δ(t)函数的筛选性质有

根据测试系统的传递关系,则
Y(ω)=H(ω)X(ω)=H(ω)
对上式两边求傅里叶逆变换可得
![]()
h(t)常被称为单位脉冲响应函数或权函数。
从以上推导可以看出,在单位脉冲信号输入的时候,时域响应函数y(t),就是脉冲响应函数h(t),而系统输出的频域函数Y(ω),就是系统的频率响应函数H(ω)。同样道理可知,系统输出的拉氏变换,就是系统的传递函数。因此,脉冲响应函数是测试系统动态传递特性的时域描述。实际上理想的单位脉冲函数是不存在的,但如果能让输入信号的幅值足够大,且其持续时间相对于系统的响应速度足够短,则测试系统便近似于对一脉冲函数作响应。实际测试时,当输入信号的作用时间小于0.1(为一阶系统的时间常数或二阶系统的振荡周期)时,则可近似地认为输入信号是脉冲信号,其响应则可视为脉冲响应函数。
对于式(2.26)所给出的一阶系统,则可由其传递函数通过拉普拉斯逆变换求得脉冲响应函数

一阶系统的单位脉冲响应曲线如图2.12(a)所示。
对于式(2.32)所给出的二阶系统(取静态灵敏度S=1,ζ<1),其脉冲响应函数为
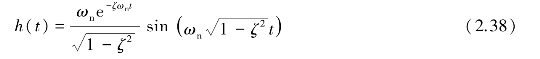
不同阻尼比的二阶系统的脉冲响应曲线如图2.12(b)所示。
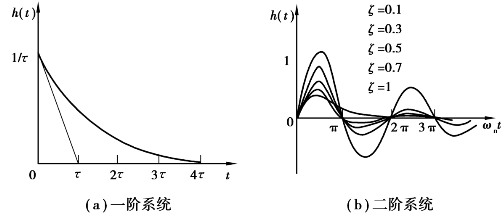
图2.12 一阶系统和二阶系统的脉冲响应函数
(2)单位阶跃输入下系统的响应函数
当输入信号为单位阶跃信号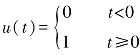 时,则一阶系统的时域响应为
时,则一阶系统的时域响应为
![]()
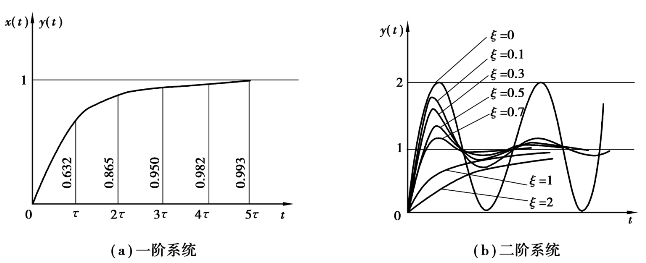
其响应曲线如图2.13(a)所示。可知,一阶系统对单位阶跃输入的稳态输出的理论误差为零,系统的初始响应速率为1/,若初始响应的速率不变,则经过时间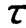 后,其输出应等于输入。但实际上响应的上升速率随时间t的增加而减慢。当t=
后,其输出应等于输入。但实际上响应的上升速率随时间t的增加而减慢。当t=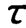 时,其输出仅达到输入量的63.2%;当t=4时,其输出才为输入量的98.2%,故
时,其输出仅达到输入量的63.2%;当t=4时,其输出才为输入量的98.2%,故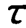 越小,响应越快,动态性能越好。通常,采用输入量的95%~98%所需要的时间作为衡量响应速度的指标。
越小,响应越快,动态性能越好。通常,采用输入量的95%~98%所需要的时间作为衡量响应速度的指标。
单位阶跃信号输入二阶系统(ζ<1)时,系统的时域响应为
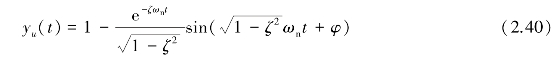
 (https://www.daowen.com)
(https://www.daowen.com)
图2.13 一阶系统和二阶系统的单位阶跃响应函数
式中
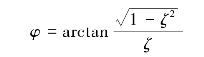
二阶系统对单位阶跃输入的响应曲线如图2.13(b)所示。其稳态输出的理论误差为零,响应则主要取决于系统的固有频率ωn和阻尼比ζ。ωn越高,系统的响应越快。阻尼比将影响超调量和振荡周期。ζ≥1时,系统蜕化为两个一阶系统串联,其阶跃响应不会产生振荡,但需要经过较长时间才能达到稳态输出,ζ越大,输出接近稳态输出的时间越长;ζ<1时,系统的输出将产生振荡,ζ越小,超调量会越大,也会因振荡而使输出达到稳态输出的时间加长。当ζ为0.6~0.8时,最大超调量为2.5%~10%。当允许误差为2%~5%时,此时达到稳态时所需的调整时间最短,为(3~4)/(ζωn)。
(3)单位斜坡输入下系统的响应
当输入信号为单位斜坡信号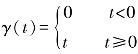 时,一阶系统的单位斜坡响应为
时,一阶系统的单位斜坡响应为
![]()
二阶系统(ζ<1)的单位斜坡响应为
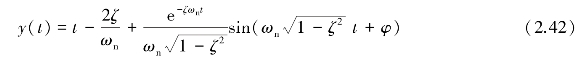
式中

一阶系统和二阶系统对单位斜坡输入的响应曲线如图2.14所示。由于输入量的不断增大,一、二阶系统的输出总是滞后于输入一段时间,存在一定的误差。随时间常数、阻尼比ζ的增大和固有频率ωn的减小,其稳态误差增大,反之亦然。
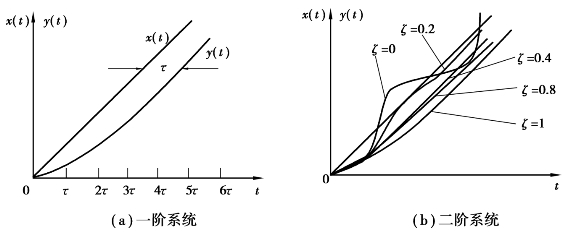
图2.14 一阶系统和二阶系统的单位斜坡响应函数
(4)单位正弦信号输入时的响应
当输入为正弦信号时,一、二阶系统的稳态输出是与输入信号同频率的正弦信号,只是输出的幅值发生了变化,相位产生了滞后。由于标准正弦信号容易获得,用不同的正弦信号激励系统,观察达到稳态时响应的幅值和相位,就可较为正确地测得幅频和相频特性,这一方法准确可靠,但需要花费较长的时间。
(5)任意输入作用下的响应
对于任意输入x(t),如果系统的脉冲响应函数为h(t),则响应y(t)为
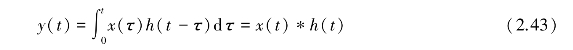
这表明测试系统的时域响应,等于输入信号x(t)与系统的脉冲响应函数h(t)的卷积。
时域中求系统的响应需要进行卷积积分运算,常采用计算机进行离散数字卷积计算,计算量较大。利用卷积定理将它转化为频域的乘积处理则相对较简单。由卷积定理可知,式(2.43)的频域表达式为
![]()
若系统为稳定的系统,输入x(t)符合傅里叶变换的条件,则也可写为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







