（1）传递函数

传递函数是在系统的初始条件为零的前提下，线性定常系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比，记为H（s）。根据拉普拉斯变换的微分性质，如果以下拉普拉斯变换存在

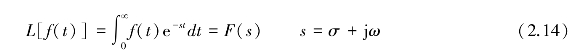
则当系统的初始条件为零时，有

利用这一性质，对式（2.1）两边作拉普拉斯变换，设输入量x（t）的拉普拉斯变换为X（s），输出量y（t）的拉普拉斯变换为Y（s），则

可得线性定常系统的传递函数

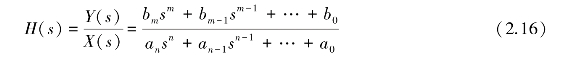
传递函数具有以下4个特点：

①传递函数H（s）只反映系统的特性，而与系统的输入x（t）以及系统的初始状态无关，即对于某一系统，其传递函数不会因其输入的变化而不同，但对任一具体输入，系统都能确定地给出相应的输出。

②传递函数H（s）是对物理系统微分方程取拉普拉斯变换求得的，它只反映系统的传输特性，而不能确定系统的物理结构。两个完全不同的物理系统可能就有相似的传递函数，如液柱式温度计和RC低通滤波器，它们虽然物理结构和性质完全不同，但传递函数形式却相似。

③传递函数中的各个系数a0，a1，…，an；b0，b1，…，bm是由测试系统本身结构特性唯一确定的常数。其量纲将因具体物理系统和输入量以及输出量的量纲的不同而不同。

④传递函数H（s）的分母取决于测试系统的结构，分母中s的最高幂次n代表测试系统微分方程的阶次；分子表示系统与外界之间的联系，如输入点的位置、输入方式、被测量及测点布置情况等。

（2）频率响应函数

传递函数是在复数域描述测试系统的特性，相比于在时域中用微分方程来描述系统特性有很多优点。但是，工程中的许多系统很难建立起微分方程和传递函数，而且传递函数的物理概念也较难理解。因此，采用在频域中描述测试系统特性的频率响应函数更为合适。频率响应函数物理概念明确，容易通过实验来建立，也可通过它求出系统的传递函数。因此，频率响应函数是实验研究测试系统的重要工具。

频率响应函数指的是系统稳态输出y（t）的傅里叶变换与输入信号x（t）的傅里叶变换之比，即

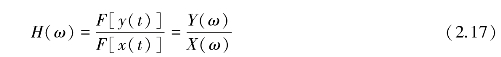
线性时不变系统可用式（2.1）所给出的常系数线性微分方程来描述。由于对于形如的函数，其n阶微分为，其傅氏变换为（jω）nX（ω）。因此，当输入信号为时，并达到稳态输出的时候，式（2.1）有以下形式的方程

由此可得

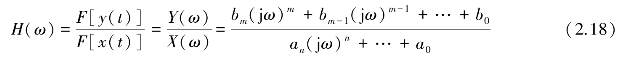
从式（2.18）可知，分母ω的幂的次数n确定了测试系统的阶数，H（ω）是由系统结构参数和测试系统的布置情况所确定的微分方程的常系数所决定的，与输入、输出本身没有关系。因此，H（ω）反映系统本身所具备的特性。对于任一具体的输入x（t），由于Y（ω）＝X（ω）H（ω），都可由系统的频率响应函数确定相应的输出y（t），因此，H（ω）反映了测试系统的传输特性。

（3）幅频特性与相频特性

一般情况下H（ω）是复函数，可将其写成为

其中

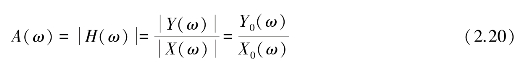
式中　A（ω）——幅频特性；

X0（ω）——输入信号的幅值；

Y0（ω）——稳态输出的幅值，则

式中　φ（ω）——相频特性；

φy（ω）——稳态输出的相位；

φx（ω）——输入信号的相位。

可见A（ω）是H（ω）的模，是给定频率点输出信号幅值与输入信号幅值之比。换句话说，给定频率点的输出信号的幅值Y0（ω）可由该频率点输入信号的幅值X0（ω）乘以A（ω）求得。因此，A（ω）相当于一个比例系数，反映测试系统对输入信号的ω频率分量的幅值的缩放能力，称A（ω）为系统的幅频特性。

φ（ω）是给定频率的输出信号与该频率输入信号的相位差，反映出测试系统对输入信号的ω频率分量的初相位的移动程度，称为测试系统的相频特性。

图2.9表示了测试系统幅频特性和相频特性对输入信号的影响。根据信号分析理论，一般的时间信号总可分解为多个不同频率成分的正弦信号。换句话说，一般的时间信号可由不同频率成分的正弦信号叠加而成。当信号通过测试系统的时候，受系统幅频特性的影响，各频率成分的幅值将会被相应频率点的系统幅频特性所缩放；受系统相频特性的影响，各频率成分的相位将发生相应的移动。得到的输出信号是由与输入信号有着相同的频率成分的正弦信号叠加而成的，但各频率成分的幅值和相位却因系统作用而发生改变。

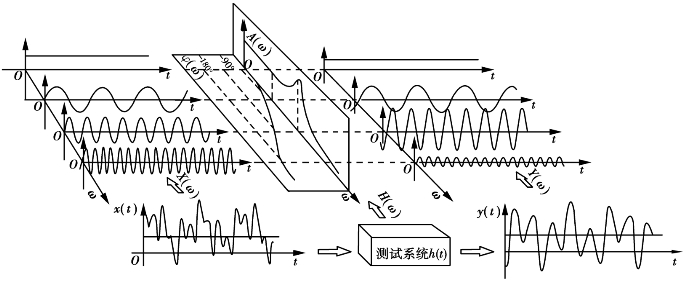
图2.9　测试系统幅频特性、相频特性对输入信号的影响

如果将H（ω）表示为实部P（ω）与虚部Q（ω）之和的形式，则H（ω）又可表示为

其幅频特性和相频特性分别为

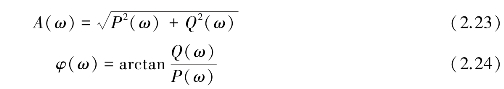
以A（ω），φ（ω），P（ω）和Q（ω）为纵坐标，ω为横坐标，分别绘出A（ω）⁃ω，φ（ω）⁃ω，P（ω）⁃ω，Q（ω）⁃ω曲线，称为幅频特性曲线、相频特性曲线、实频特性曲线、虚频特性曲线。

在工程应用技术中，对于幅频特性曲线和相频特性曲线的纵坐标、横坐标除了取线性标尺外，还常对自变量ω取对数标尺，幅值取分贝数，画出的20 lg A（ω）⁃lg ω曲线和φ（ω）⁃lg ω曲线，分别称为对数幅频特性曲线和对数相频特性曲线。两种曲线总称为伯德（Bode）图。

如果以H（ω）的实部和虚部分别作为横坐标和纵坐标，在此复平面画出Q（ω）⁃P（ω）曲线，并在曲线对应点上标注相应的频率，则所得曲线图称为奈魁斯特图（Nyquist图）。

（4）传递函数与频率响应函数的关系

传递函数与频率响应函数之间有着密切的内在联系，这种内在联系源于傅氏变换与拉氏变换的关系，由傅里叶变换的定义式可知，频率响应函数只不过是传递函数的一种特例，是s＝jω时的传递函数。因此，频率响应函数可以在求得传递函数之后，取s＝jω即可。(www.daowen.com)

传递函数和频率响应函数都可表示系统的传递特性，但两者的含义不同。推导传递函数时，系统的初始条件为零。而对于一个从t＝0时刻开始施加的简谐信号来说，通过拉普拉斯变换解得的系统输出包含瞬态输出和稳态输出两部分。系统在受到激励后有一段过渡过程，经过一定的时间后，系统的瞬态输出趋于定值，进入稳态输出。频率响应函数表达的是系统对简谐输入信号的稳态输出。在观察时，系统的瞬态输出已经趋于零。因此，用频率响应函数不能反映响应的过渡过程，而传递函数则能反映响应的全过程。但频率响应函数能直观地反映系统对不同频率输入信号的响应特性。

在实际的工程技术问题中，为了获得较好的测量效果，常在系统处于稳态输出的阶段上进行测试。在测试工作中，常用频率响应函数来描述测试系统的动态特性。而控制系统要研究的是典型扰动引起控制系统的响应，研究一个过程从起始的瞬态变化过程到最终的稳态过程的全部特性。因此，在控制工程中常用传递函数来描述控制系统的动态特性。

（5）一阶系统的传递函数与频率响应函数

如图2.3所示的RC低通滤波电路，以及无质量的弹簧阻尼系统、液柱式温度计测温系统等，都属一阶系统。其运动微分方程的一般形式

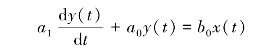
对于以上的微分方程，可将其改写成标准归一化的形式

式中　——时间常数，＝a1/a0，具有时间的量纲；

S——静态灵敏度，S＝b0/a0，由具体的系统参数决定。

线性系统中S为常数，在对系统的特性作动态分析时，它仅仅使系统的传递特性放大S倍，而不会改变特性曲线的变化规律。为了讨论和分析的方便，突出系统的特性，约定S＝1，则式（2.25）可写为

对上式作拉氏变换得

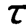sY（s）＋Y（s）＝X（s）

则一阶系统的传递函数为

令s＝jω，其频率响应函数为

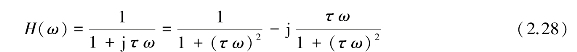
则其幅频特性和相频特性函数分别为

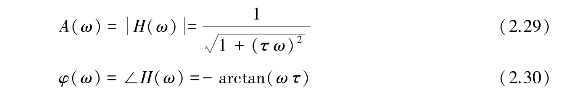
根据式（2.29）和式（2.30）绘出幅频曲线和相频曲线如图2.10所示。

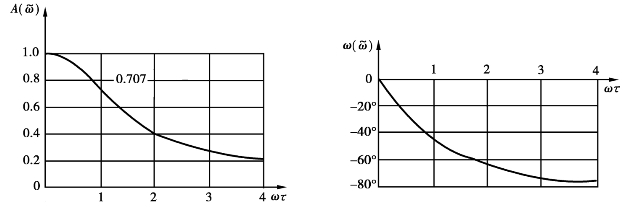
图2.10　一阶系统的幅频特性曲线和相频特性曲线

从频率响应特性图上可以看出，一阶系统有以下两个特点：

①一阶系统是一个低通环节，当ω远小于1/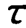时（约ω＜1/5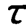），幅频特性A（ω）近似为1（误差不超过2％）。信号通过系统后，各频率成分的幅值基本保持不变。在高频段，幅频特性与ω成反比，其水平渐近线为A（ω）＝0，此时的一阶系统，演变成为积分环节。从图2.10可以看出，当ω＞4/时，A（ω）＜0.25，且存在较大的相差，信号通过系统，各频率成分的幅值将有很大的衰减。因此，一阶装置只适用于测量缓变的低频信号。

②时间常数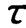决定了一阶系统适用的频率范围，从幅频特性曲线和相频特性曲线可以看出，当ω＝1/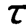时，输出输入的幅值比A（ω）降为0.707（－3dB），此点对应着输出信号的功率衰减到输入信号半功率的频率点，被视为信号通过系统的截止点。因此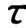，是反映一阶系统动态特性的重要参数。

（6）二阶系统的传递函数与频率响应函数

典型的二阶系统有质量⁃弹簧⁃阻尼系统、RLC电路系统、测力弹簧秤等，二阶系统可用二阶常系数微分方程表示，即

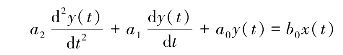
通过数学处理可使其变为以下标准归一化的形式

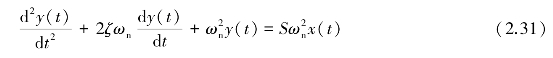
式中　ωn——系统的固有频率，；

ζ——系统的阻尼比，；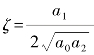

S——系统的灵敏度系数，S＝b0/a0。

S是取决于输出与输入量纲和比值的常数因子，不会改变特性曲线的变化规律，对相频特性也没有影响。因此，约定取S＝1，则二阶系统的传递函数为

二阶系统的频率响应函数为

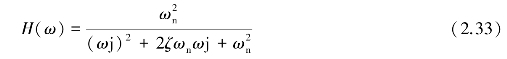
将式（2.33）分子和分母同除以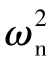，并令η＝ω/ωn，则

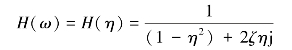
二阶系统的幅频特性和相频特性分别为

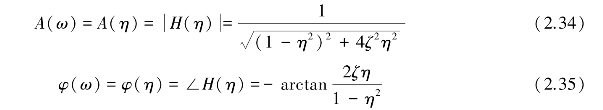
相应的幅频、相频特性曲线如图2.11所示。

二阶系统具有以下的特点：

①当ω≪ωn时，A（ω）≈1，φ（ω）很小；当ω≫ωn时，A（ω）→0，φ（ω）接近－180°。因此，二阶系统也是低通环节。

②当ω＝ωn时，幅频特性曲线出现峰值，系统将发生“共振”。在进行测试时，要避开“共振区”工作。但可利用共振来确定测试系统本身的参数。发生共振时，即当ω＝ωn时，A（ω）＝1/（2ζ），φ（ω）＝－90°，并且不会因阻尼比的不同而改变。

由一阶系统和二阶系统的频率响应可以看出，一阶系统的灵敏度系数S、时间常数，二阶系统的灵敏度系数S、固有频率ωn、阻尼比ζ是由系统的结构参数决定的。当测试系统制造、调试完成之后，其参数就随之确定了。

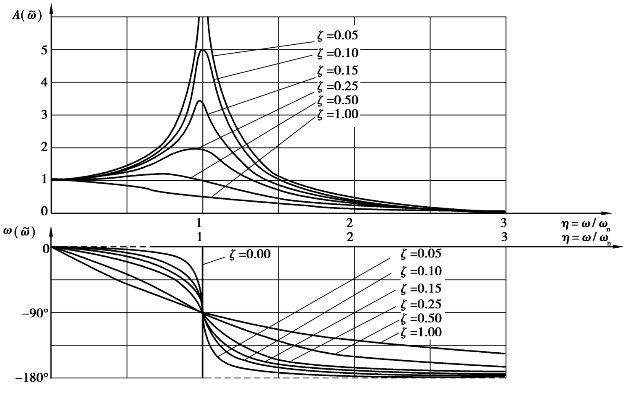
图2.11　二阶系统的幅频特性曲线和相频特性曲线