描述测试系统通常是通过对测试系统的数学建模，利用测试系统的物理特性建立系统输入、输出的运动微分方程实现系统的数学描述。较复杂的系统，其数学模型可能是一个高阶微分方程，微分方程的阶数就是系统的阶数。下面通过对几个简单的测试系统的分析，说明测试系统的描述和系统输入、输出之间的联系。

图2.3是一个RC低通滤波系统，其输入电压为x（t），输出电压为y（t），根据电路电压平衡关系为

x（t）＝R·i（t）＋y（t）

设流经电阻和电容的电流为i（t），则

据此，可建立x（t）和y（t）之间的运动微分方程为

这是一个一阶常系数线性微分方程，由于决定微分方程的系统结构参数R、C是不随时间改变的常数，系统的响应与激励施加于系统的时刻无关。因此，该微分方程描述的系统是一阶线性时不变系统。常见的一阶线性时不变系统还有忽略质量的弹簧阻尼系统、液柱式温度计测温系统等。

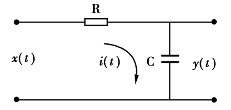
图2.3　RC低通滤波系统

(www.daowen.com)

图2.4　质量⁃弹簧⁃阻尼系统　

如图2.4所示为一个质量⁃弹簧⁃阻尼系统。f（t）为作用在质量块上的力，是系统的输入；x（t）为质量块的位移，是系统的输出。对质量块进行受力分析，根据牛顿第二定律可得，系统的运动微分方程为

式中　m——质量块的质量；

c——阻尼器的阻尼系数；

k——弹簧的刚度系数。

该运动微分方程为一个二阶常系数微分方程，所以该质量⁃弹簧⁃阻尼系统为一个二阶线性时不变系统。电工学中的RLC电路也是常见的二阶系统。

对于线性时不变系统，可用输入x（t）、输出y（t）之间的常系数线性微分方程来描述。其微分方程的一般形式为

式中，an，an－1，an－2，…，a0和bm，bm－1，bm－2，…，b0是与测试系统的物理特性、结构参数和输入状态有关的常数；n和m为正整数，表示微分的阶，一般n≥m，并称n值为线性系统的阶数。