（1）时域卷积定理

如果

则

证：

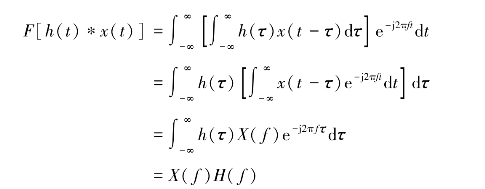
时域卷积定理说明两个时间函数卷积的频谱等于各个时间函数频谱的乘积，即在时域中两信号的卷积，等效于在频域中频谱相乘。

例1.10　用时域卷积定理研究两个矩形脉冲信号h（t）和x（t）的卷积与傅里叶变换的关系。

如图1.30所示，两个矩形函数的卷积是如图1.30（e）所示的三角形函数；单个矩形函数的傅里叶变换是如图1.30（c）、（d）所示的sin c（t）型函数。根据时域卷积定理：时域中的卷积对应于频域中的乘积，可知图1.30中三角形与［sin c（t）］2型函数是一个傅里叶变换对。此例可以说明，时域卷积定理是分析其他傅里叶变换对的一个方便的工具。

例1.11　研究脉冲序列h（t）与矩形脉冲x（t）的卷积与傅里叶变换之间的关系，如图1.31所示。

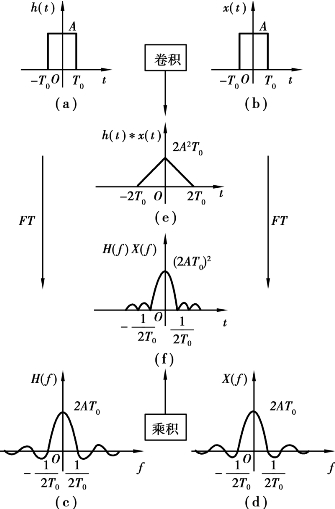
图1.30　两矩形脉冲信号的卷积与傅里叶变换的关系

(www.daowen.com)

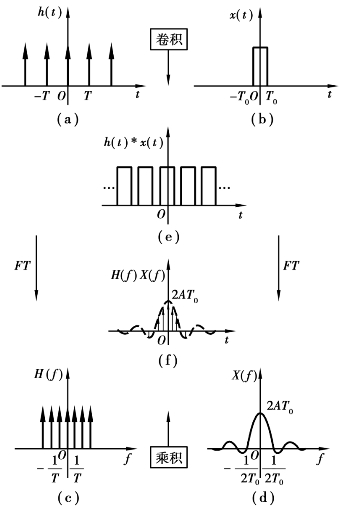
图1.31　脉冲序列与矩形脉冲的卷积与傅里叶变换之间的关系

脉冲序列h（t）与单个矩形脉冲的卷积为矩形脉冲序列，如图1.30（e）所示；脉冲序列h（t）的傅里叶变换仍为脉冲序列，如图1.30（c）所示；矩形脉冲函数的傅里叶变换为sin c（t）型函数，如图1.30（d）所示；由时域卷积定理，时域卷积的傅里叶变换对应于频域乘积，故而矩形脉冲序列的傅里叶变换，是幅度被sin c（t）型函数所加权的脉冲序列，如图1.30（f）所示。

从以上两例分析中，可了解到信号的卷积与傅里叶变换之间的关系，并且也可知，非周期信号（如矩形脉冲、三角脉冲）的傅里叶变换是连续频谱，而周期信号（脉冲序列）的傅里叶变换是离散谱。

（2）频域卷积定理

如果

F［h（t）］＝H（f），F［x（t）］＝X（f）

则

频域卷积定理说明两时间函数的频谱的卷积等于时域两函数的乘积的傅里叶变换，即在时域中两信号的乘积等效于在频域中频谱的卷积。

例1.12　利用频域卷积定理来研究余弦信号截断后的频谱，如图1.32所示。

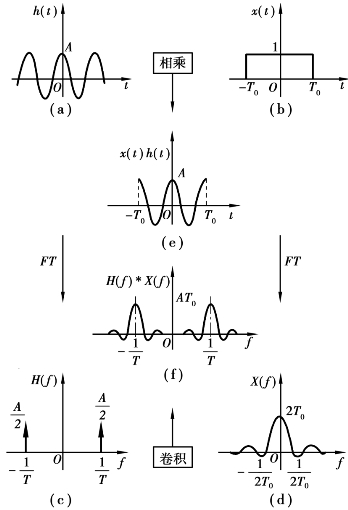
图1.32　截断余弦信号的傅里叶变换

余弦信号h（t）与矩形函数x（t）相乘，得到余弦的截断信号，如图1.32（e）所示；余弦信号的傅里叶变换是δ函数，如图1.32（c）所示；矩形函数的傅里叶变换是sin c（t）型函数，如图1.32（d）所示；H（f）与X（f）的卷积是sin c（t）型函数被移至δ函数点重新构图，如图1.32（f）所示，它是h（t）与x（t）乘积的傅里叶变换。

此例表明了无限长余弦信号的频域能量集中在－1/T与1/T点，而截断后的余弦信号的频域能量则在－1/T与1/T点附近分散。