（1）信号的自相关函数Rx（）

假如信号x（t）是随机信号的一个样本记录，x（t＋）是x（t）延时后的样本，则对于各态历经的随机过程，其自相关函数Rx（）可定义为

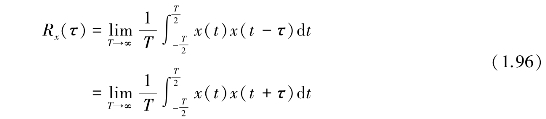
式中　T——样本记录时间，即观测时间。

根据自相关函数的定义，可得出自相关函数的几个重要性质。

①自相关函数是的偶函数，即

②自相关函数在＝0时为最大值，并等于该信号的均方值。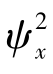

③周期信号的自相关函数仍然是同频率的周期信号，并保留了原信号的幅值信息，但不具有原信号的相位信息。

④随机信号的自相关函数将随值增大而很快衰减。当随机信号的均值为零时，Rx（）将衰减至零；当随机信号的均值为μx时，Rx（）将衰减至。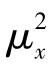

例1.6　求正弦信号x（t）＝A sin（ω0t＋φ）的自相关函数。

解　该正弦信号为一周期信号，周期T0＝2π/ω0，即

根据三角公式

所以

又因为

故

可见正弦函数的自相关函数是一个余弦函数，在＝0处具有最大值。它保留了原正弦信号的幅值信息和频率信息，但丢失了原正弦信号的初始相位信息。

图1.25是4种典型信号的自相关函数，可以看出自相关函数是区别信号类型的一个非常有效的手段，只要信号中含有周期成分，其自相关函数在很大时都不衰减，并具有明显的周期性。不包含周期成分的随机信号，当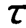稍大时其自相关函数就将趋于零。宽带随机噪声的自相关函数很快衰减到零，窄带随机噪声的自相关函数则有较慢的衰减特性。

图1.25　4种典型信号的自相关函数图形

（2）信号的互相关函数Rxy（）

两个各态历经随机信号x（t）和y（t）的互相关函数Rxy（）定义为(www.daowen.com)

互相关函数有以下一些性质：

①互相关函数为非奇非偶函数，但满足下式

②两周期信号的互相关函数仍然是同频率的周期信号，且保留了原信号的相位差信息和幅值信息。

③两个非同频的周期信号互不相关。

例1.7　设有两个周期信号x（t）和y（t）

x（t）＝A sin（ω0t＋θ）　　　　y（t）＝B sin（ω0t＋θ－φ）

式中，θ为x（t）相对于t＝0时刻的相位角；φ为x（t）与y（t）的相位差。试求其互相关函数Rxy（）。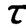

解　因为两信号是同频率的周期函数，其周期为T0＝2π/ω0，则

根据三角公式

所以

又因为

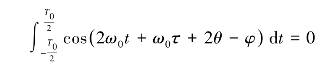
所以最后求得

由例1.7可见，两个均值为零且有相同频率的周期信号，其互相关函数中保留了这两个信号的圆频率ω0、对应的幅值A和B以及相位差值φ的信息。

例1.8　若两个周期信号x（t）和y（t）的圆频率不等

x（t）＝A sin（ω1t＋θ）　　　　y（t）＝B sin（ω2t＋θ－φ）

试求其互相关函数。

解　因为两信号的圆频率不等（ω1≠ω2），不具有共同的周期，因此，按式（1.98）计算

由此可见，两个非同频率的周期信号是不相关的。