随机信号不能用确定的数学关系式来描述，也无法预测其未来某一时刻的精确值。对于随机信号，每一次观测结果都不一样，每一次观测结果都只是许多可能产生的结果中的一种，但是其观测值的变动服从统计规律，必须用概率和统计的方法来描述。如果某随机信号是各态历经随机信号，则该随机信号的统计特征参数主要有均值、均方值、均方根值、方差及概率密度函数。也可利用相关函数对各态历经随机信号进行描述。如要从频率域对各态历经随机信号进行描述，则可用自功率谱密度函数、互谱密度函数和相干函数。

（1）随机信号的自功率谱密度函数

设x（t）为一个均值为零的随机信号，由于随机信号的持续期为无限长，不满足绝对可积与能量有限条件。因此，它的傅里叶变换不存在。但是，随机信号的平均功率却是有限的，即有

因此，可研究随机信号的功率谱。

为了将傅里叶变换方法应用于随机信号，必须对随机信号做某些限制。最简单的一种方法是先对随机信号进行截断，再进行傅里叶变换，这种方法称为随机信号的有限傅里叶变换。

设x（t）为任一随机信号，如图1.23所示。现任意截取其中长度为T（T为有限值）的一段信号，记为xT（t），称作x（t）的截取信号，即

随机信号x（t）的截取信号xT（t）满足绝对可积条件，xT（t）的傅里叶变换存在，有

图1.23　随机信号及其截断

和

随机信号x（t）在时间区间内的平均功率为

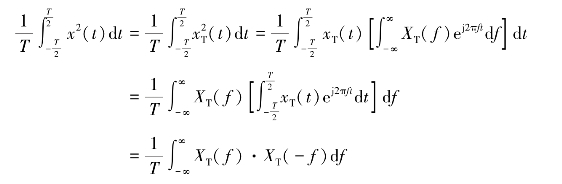
因为x（t）为实函数，则，所以

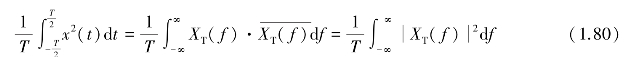
令T→∞，对式（1.80）两边取极限，便可得到随机信号的平均功率

令

则

由式（1.83）可看出，Sx（f）描述了随机信号的平均功率在各个不同频率上的分布，称为随机信号x（t）的自功率谱密度函数，简称自谱密度。其量纲为EU2/Hz，EU为随机信号的工程单位。式（1.82）对应的估计式为

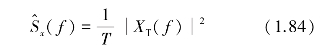
图1.24　单边与双边自功率谱密度

式（1.82）中自谱密度Sx（f）是定义在所有频率域上，一般称为双边谱。在实际中，更多使用定义在非负频率上的谱，这种谱称为单边自功率谱密度函数Gx（f）（见图1.24）。其定义为

(www.daowen.com)

（2）两随机信号的互谱密度函数

与定义自功率谱密度函数一样，可用两个随机信号x（t）和y（t）的有限傅里叶变换来定义x（t）和y（t）的互谱密度函数Sxy（f），即

实际分析中是采用估计式

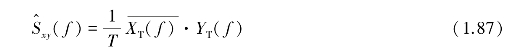
进行近似计算。

Sxy（f）为双边谱，其对应的单边谱Gxy（f）定义为

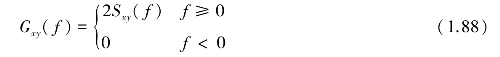
互谱密度函数是一个复数，常用实部和虚部来表示，即

在实际中，常用互谱密度函数的幅值和相位来表示，即

互谱密度函数表示出了两信号之间的幅值和相位关系。但是，互谱密度函数不像自谱密度函数那样具有功率的物理涵义，引入互谱这个概念是为了能在频率域描述两个平稳随机过程的相关性。在工程实际中，常利用测定线性系统的输出与输入的互谱密度函数来识别系统的动态特性。

（3）相干函数与频率响应函数

利用互谱密度函数可以定义相干函数（f）及系统的频率响应函数H（f），即

相干函数（coherence function）又称凝聚函数，是谱相关分析的重要参数，特别是在系统辨识中相干函数可判明输出y（t）与输入x（t）的关系。

相干函数（f）是一个无量纲函数，它的取值范围为［0，1］。当（f）＝0时，表明y（t）与x（t）不相干，即输出y（t）不是由输入x（t）引起；当（f）＝1时，说明y（t）与x（t）完全相干；当0＜（f）＜1时，有以下3种可能：

①测试中有外界噪声干扰。

②输出y（t）是输入x（t）和其他输入的综合输出。

③联系x（t）和y（t）的系统是非线性的。

频率响应函数H（f）是由互谱与自谱的比值求得的。它是一个复矢量，保留了幅值大小与相位信息，描述了系统的频域特性。对H（f）作傅里叶逆变换，即可求得系统时域特性的单位脉冲响应函数h（t）。

（4）巴塞伐尔定理

假设

则有

式（1.95）即为巴塞伐尔定理，它表明信号在时域中计算的总能量等于其在频域中计算的总能量，故又被称为信号能量等式。|X（f）|2被称为能量谱，它是沿频率轴的能量分布密度。

根据信号功率（或能量）在频域中的分布情况，随机过程可分为窄带随机、宽带随机和白噪声等类型。窄带随机过程的功率谱（或能量）集中于某一中心频率附近，宽带随机过程的能量则分布在较宽的频率上，白噪声过程的能量在所分析的频域内呈均匀分布状态。