最简单的周期信号是正弦信号或余弦信号,设某正弦信号为
![]()
式中 A——正弦信号的幅值;
θ——正弦信号的相位,rad;
ω——正弦信号的圆频率,rad/s;
f——正弦信号的频率,Hz。
如果正弦信号的周期为T,则

(1)傅里叶级数的三角函数展开式
在有限区间上,凡满足狄里赫利条件,即,信号在一个周期内连续或只含有有限个间断点的周期信号x(t)都可展开成傅里叶级数。傅里叶级数展开式有两种形式:三角函数展开式和复指数展开式。傅里叶级数的三角函数展开式为
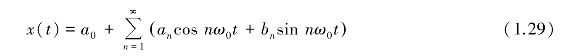
式中

式中,a0代表了信号x(t)在积分区间内的均值,被称为常值分量或直流分量。
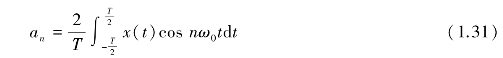
它是第n次谐波分量余弦项的值,被称为余弦分量。
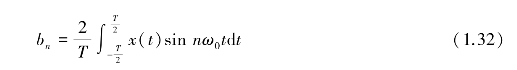
它是第n次谐波分量正弦项的值,被称为正弦分量。
式中 T——基本周期;
ω0——圆频率,![]() ;
;
n=1,2,3,…。
将式(1.29)中同频分量合并,可改写为

式中

将式(1.29)中同频分量合并,也可写为
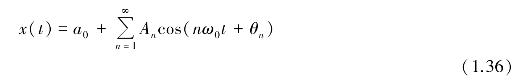
式中,An与式(1.34)相同,则

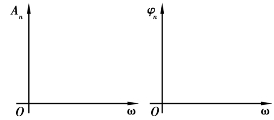
图1.13 幅值谱图和相位谱图坐标
从式(1.33)和式(1.36)可以看出,周期信号是由一个或几个、乃至无穷多个不同频率的谐波叠加而成的。通常把ω0称为基频,并把成分Ansin(nω0t+φn)称为n次谐波。An被称为第n次谐波的幅值,φn被称为第n次谐波的相位。以圆频率ω为横坐标,幅值An或相角φn为纵坐标作图(见图1.13),可分别得到周期信号的幅值谱图和相位谱图。由于n是整数序列,各频率成分都是ω0的整倍数,相邻频率的间隔Δω=ω0=2π/T,因而周期信号的谱线是离散的。
(2)傅里叶级数的复指数展开式
傅里叶级数也可写成复指数形式。利用欧拉(Euler)公式
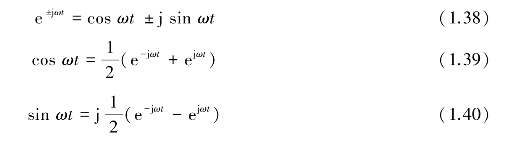
式中,![]() ,式(1.29)可改写为
,式(1.29)可改写为
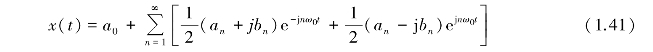
令 c0=a0

则

或(https://www.daowen.com)
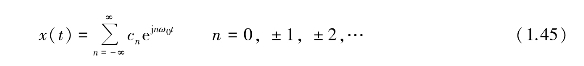
式中
![]()
一般情况下,系数cn是一个以谐波次数n为自变量的复值函数,它包含了第n次谐波的振幅和相位信息,即
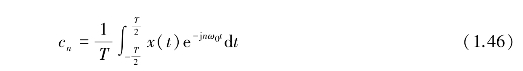
式中
![]()

cn与c-n共轭,即
![]()
把周期函数x(t)展开为傅里叶级数的复指数函数形式后,可分别以|cn|-ω和φn-ω作幅值谱图和相位谱图;也可分别以cn的实部和虚部与频率的关系,即cnR-ω和cnI-ω,作幅值谱图,分别称为实频谱图和虚频谱图。
傅里叶级数复指数展开式与三角函数展开式相比主要的区别在于,复指数函数形式的频谱为双边幅值谱(ω从-∞到+∞),三角函数形式的频谱为单边幅值谱(ω从0到+∞);这两种频谱各次谐波在量值上有确定的关系,即c0=a0, 。双边幅值谱为偶函数,双边相位谱为奇函数。
。双边幅值谱为偶函数,双边相位谱为奇函数。
负频率是与负指数相关联的,是数学运算的结果,并无确切的物理含义,在工程实际中是不存在的。
例1.1 求如图1.14所示周期性三角波的傅里叶级数表示。
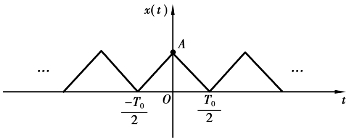
图1.14 周期三角波
解 x(t)在一个周期内的数学表达式为

常值分量
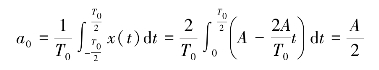
余弦分量的幅值
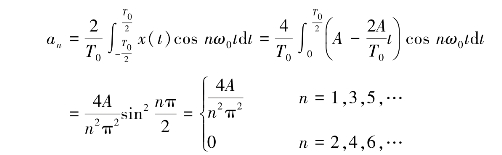
正弦分量的幅值
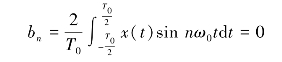
这样,该周期性三角波的傅里叶级数展开式为
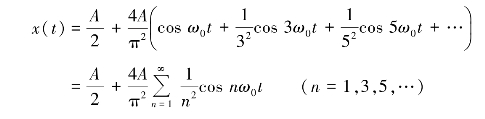
周期性三角波的频谱图如图1.15所示。其幅值谱只包含常值分量、基波和奇次谐波的频率分量,谐波的幅值以![]() 的规律收敛。在其相位谱中,基波和各次谐波的初相位φn均为零。
的规律收敛。在其相位谱中,基波和各次谐波的初相位φn均为零。
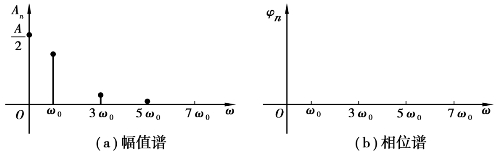
图1.15 周期三角波的频谱
例1.2 画出余弦、正弦信号的实频谱图和虚频谱图。
解 根据式(1.39)和式(1.40)得
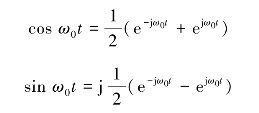
故余弦信号只有实频谱,与纵轴偶对称。正弦函数只有虚频谱图,与纵轴奇对称。图1.16是这两个函数的频谱图。
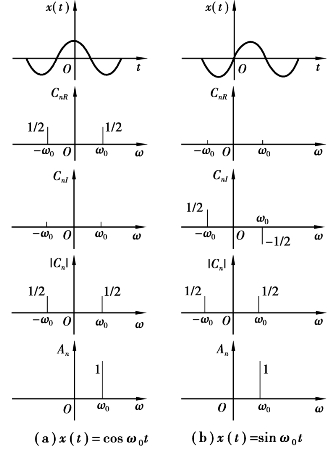
图1.16 余弦函数和正弦函数的频谱
从上例还可得到以下推论:一般周期实函数按傅里叶级数的复指数展开后,其实频谱(对应三角函数展开中的余弦分量)总是偶对称的,其虚频谱(对应三角函数展开中的正弦分量)总是奇对称的。更进一步,若周期实函数为实偶函数,则其傅里叶级数的复指数展开将只有偶对称的实部,若周期函数为实奇函数,则其傅里叶级数的复指数展开将只有奇对称的虚部。
(3)周期信号频谱的特点
周期信号的频谱具有以下特点:
①周期信号的频谱是离散的。
②每条谱线只出现在基波频率的整倍数上,基波频率是各高次谐波分量频率的公约数。
③各频率分量的谱线高度表示该次谐波的幅值和相位角。谱线的高度也代表了该次谐波的能量大小。工程中常见的周期信号,其谐波分量的幅值总的趋势是随谐波次数的增高而减小。因此,在频谱分析中可根据精度的需要决定所计算谐波的次数,没有必要取那些次数过高的谐波分量。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







