通过对足底按照如表5-8分区的方式，穿三种软硬不同的鞋底的鞋，测力鞋垫在鞋底上，在跑台上匀速步行60min，从开始步行每隔5min记录一次数值，到步行结束为止共记录13组数据，所得的数据如表5-8所示。

表5-8　穿不同鞋的最大力值、峰压强值、冲量以及接触面积　(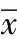±s)

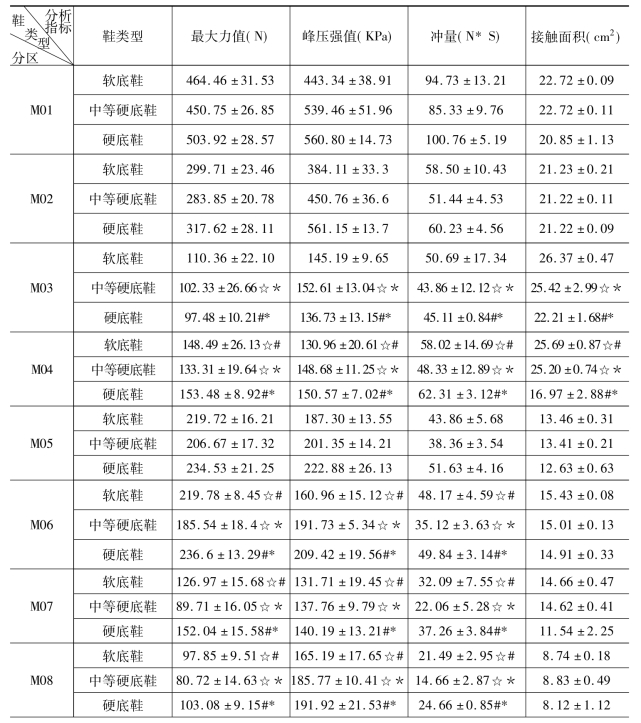
续表

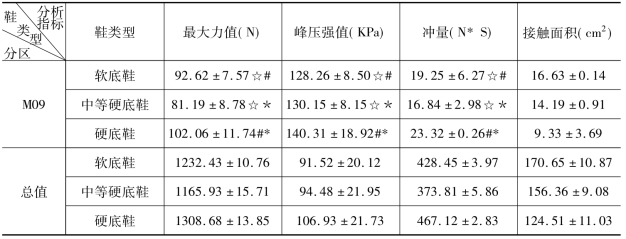
注 软底鞋与中等硬底鞋有差异☆，软底鞋与硬底鞋有差异#，中等硬底鞋与硬底鞋有差异*。

(一)穿不同鞋的足底分区的压力

对足底压力的研究，可以揭示人体运动过程中足的动力学特征。正常步态从脚跟触地到全脚掌支撑再到前脚掌蹬离地面，足底压力的部位和大小都随着时间的改变而改变。

若足部各区压力分布均匀，可以降低运动伤害，而足底压力为最大压力和最小压力的范围越小越好;足底压力测量显示出，如在足部某一部位，承受过大压力时，即易产生过度使用伤害。

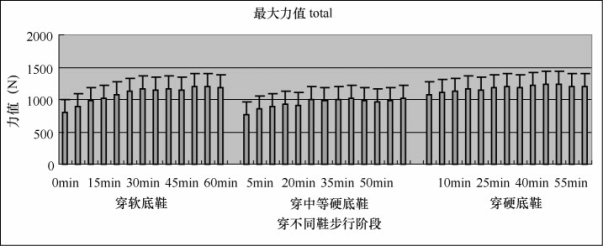
图5-32　足底最大力值(总合)

如图5-32所示，软底鞋、中等硬底鞋开始没有迅速达到最大力变量值，而是递增的，从15min后才达到平稳，总体来看，最大力值呈现如下规律——硬底鞋大于软底鞋，软底鞋大于中等硬底鞋。我们认为足底压力依时间变化呈现某种上升或下降的趋势，可以找到一条适当的函数曲线来反映这种变化趋势，即以时间t为自变量，力值时间序列y为因变量，建立趋势方程:

软底鞋的趋势方程为y=576.59x0.0896，拟合优度R2=0.8587，中等硬底鞋的趋势方程为y=728.964x0.08821，拟合优度R2=0.7917，硬底鞋的趋势方程为y=789.02x0.1035，拟合优度R2=0.8977。可见三双鞋的足底压力依时间变化呈现上升趋势，并且硬底鞋的要高于其他两双鞋。

1.足底最大力值分析

从图5-33中可以看出，足跟内侧(M01)的最大力值，软底鞋和中等硬底鞋呈现随时间增加的趋势，而硬底鞋表现出随时间波动。通过相关性分析，穿三双鞋，总的最大力值与M01均有相关性。

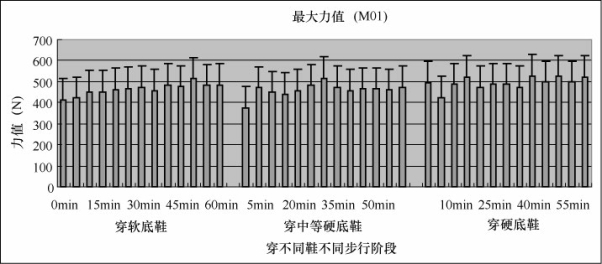
图5-33　足底最大力值(M01)

从图5-34中可以看出，足跟外侧(M02)的最大力值，三双鞋都随着时间表现出波动，软底鞋和硬底鞋总体都是呈现增长，而中等硬底鞋开始和结束值的大小一样。通过相关性分析，穿中等硬底鞋时，最大力值与M02有相关性。

从图5-35中可以看出，足弓内侧(M03)的最大力值，软底鞋和中等硬底鞋开始都比较低，到第15min后都增长到比较大的值，随后软底鞋缓慢增长，中等硬底鞋有所回落。而硬底鞋刚开始力值比较高之后就降低到一个比较稳定的值，基本不变。通过相关性分析，穿三双鞋最大力值与M03有相关性。

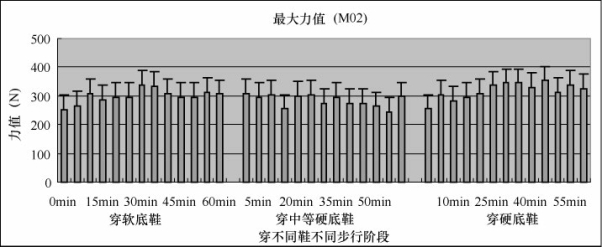
图5-34　足底最大力值(M02)

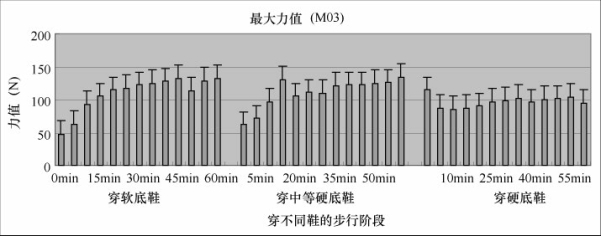
图5-35　足底最大力值(M03)

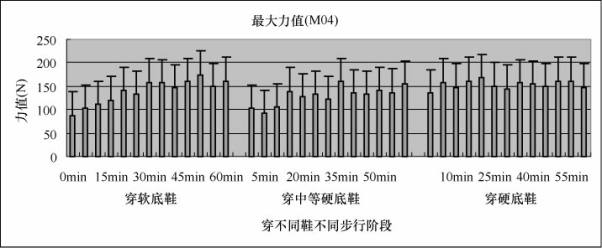
图5-36　足底最大力值(M04)

从图5-36中可以看出，足弓外侧(M04)的最大力值，软底鞋和中等硬底鞋开始都比较低，随时间的增长而呈现上升的趋势，而硬底鞋开始就比较高，随时间变化不是很大。通过相关性分析，穿三双鞋时，最大力值与M04有相关性。

从图5-37中可以看出，以蹬伸为主要功能的第一跖骨区(M05)的最大力值，软底鞋和中等硬底鞋随时间虽然有所波动但总体上没有什么变化，硬底鞋开始5min力值比较大，随时间而呈现下降的趋势。

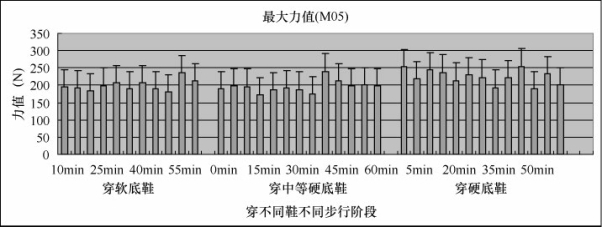
图5-37　足底最大力值(M05)

从图5-38中可以看出，第二、第三跖骨区(M06)的最大力值，软底鞋和硬底鞋开始值比较高，并且随时间增长总体上没有什么变化，而中等硬底鞋值比较小，随时间呈增大的趋势。

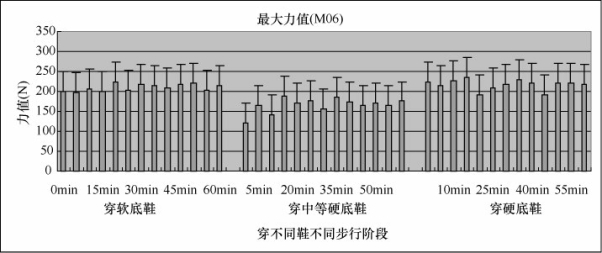
图5-38　足底最大力值(M06)

通过相关性分析，穿三双鞋时，最大力值M06有相关性。并且通过方差分析，我们发现在M06，三双鞋之间均有差异。

从图5-39中可以看出，第四、第五跖骨区(M07)的最大力值，软底鞋和硬底鞋开始值比较高，而中等硬底鞋开始值比较小，但三双鞋在此区的最大力值都随时间呈增大的趋势。通过相关性分析，穿三双鞋时，最大力值与M07有相关性。并且通过方差分析，我们发现在M07，三双鞋之间均有差异。

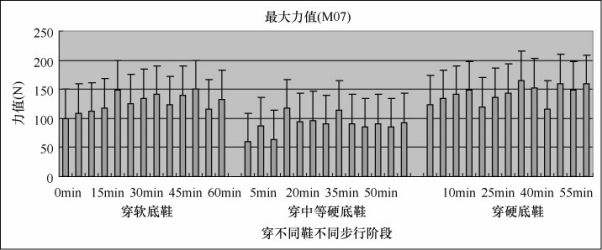
图5-39　足底最大力值(M07)

从图5-40中可以看出，第一趾骨(M08)的最大力值，软底鞋和硬底鞋开始值比较高，而中等硬底鞋开始值非常小，5min后迅速增长，随时间增长三双鞋均有所波动，软底鞋下降，中等硬底鞋升高，硬底鞋基本不变。

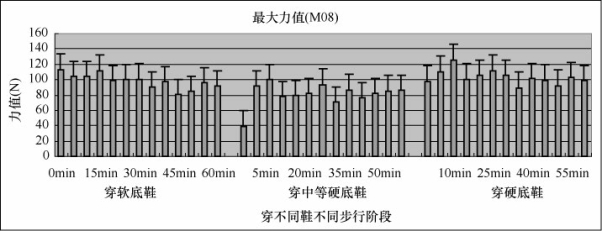
图5-40　足底最大力值(M08)

通过相关性分析，穿中等硬底鞋时，最大力值与M08有负相关性。并且通过方差分析，我们发现在M08，三双鞋之间均有差异。

从图5-41中可以看出，第二～第五趾骨(M09)的最大力值，三双鞋随时间波动，但均变化不太大。并且通过方差分析，我们发现在M09，三双鞋之间均有差异。

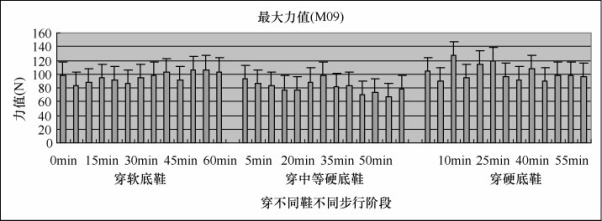
图5-41　足底最大力值(M09)

软底鞋和中等硬底鞋之间，M06，M07，M08，M09之间有差异，可见不同鞋底之间，前半段之间有差异，即穿软底鞋和软硬度适中的鞋底相比，对足弓和足跟影响不是很大，但是对足的前半段影响比较明显。

2.足底的分区力值的因子分析

我们在实验中将足底分为九个区，需要处理的相关变量比较多，为了将大量的变量减少成少数几个互相独立的线性组合变量，亦即潜在变量或成分，我们以中等硬底鞋为例，采取多元统计分析中处理降维问题的因子分析。具体分析如下:

KMO值为0.788，在0.5～1之间，表示适合做因子分析。

从表5-9中可以看出，左边9个成分因素的特征值总和等于9。解释变异量为特征值除以变量数目，如第一个特征值的解释变异量为5.556/9=61.733%，第二个特征值的解释变异量为1.752/9=19.462%，累积的解释变异量为81.195%(达到80%，故只需要提取两个公共因子)。从陡坡图5-42中可以看出，从第二个因素后，坡线变为平坦，因而以保留两个因素较为适宜。

表5-9　中等硬底鞋的总方差解释表

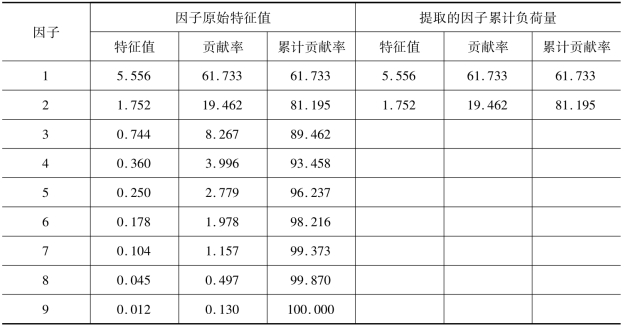
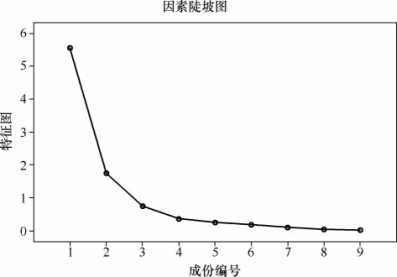
图5-42　中等硬底鞋的因素陡坡图

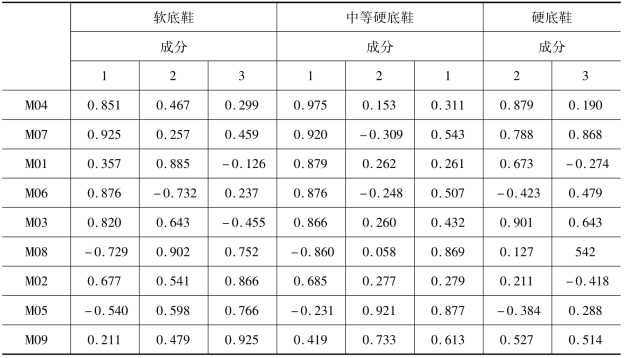
表5-10　软底鞋的方差最大正交旋转后的因子载荷阵

由旋转后的正交因子载荷阵(表5-10)可知:

第一公共因子上(第一行)高载荷的指标有M04、M07、M01、M06、M03，相应的因子载荷值分别为0.975、0.920、0.879、0.876、0.866，这些分区均为落地缓冲所必需的几个方面，故将第一公共因子F1命名为基本落地缓冲因子。

而第二公共因子上(第二行)高载荷的指标有M05，相应的因子载荷值为0.921，这个分区反映了足底在步行阶段蹬伸的需求，因此将第二公共因子F2命名为蹬伸因子。

图5-43显示了因素负荷载量，可绘出九个原始变量在萃取的两个因素的散点图，此图为旋转后因素矩阵的散点图。从图中可清楚地看出转轴后的效果相当好，第一公共因子F1属于第一因素的横轴，第二公共因子F2属于因素二的纵轴。(www.daowen.com)

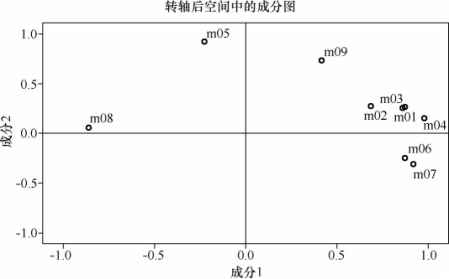
图5-43　中等硬底鞋的因素负荷量

另外，我们通过对其他两双鞋做因子分析，得出以下的因子分析表5-11。

从因子分析表中，我们可以看出，中等硬底鞋有两个因子，而软底鞋和硬底鞋均有三个因子，软底鞋的M07、M06、M04、M03四区为一个主成分，M08和M01两区为一个主成分，可以解释为内翻因子，M09和M02两区为一个主成分，可以解释为外翻因子，说明这双鞋对足底的内外翻影响比较大;硬底鞋的M05、M08两区为一个主成分，M03和M04两区为一个主成分，M07为一个主成分，说明这双鞋对蹬地、足弓以及外侧跖骨影响比较大。

表5-11　三双鞋的方差最大正交旋转后的因子载荷阵

(二)穿不同鞋的足底分区的压强

足底压力测量显示出，若在足底局部某一位置承受过大压强时，会产生过度使用对足底的伤害;最大足底压强往往和前足病变有极高的相关性，因而必须防止高压强区的出现。步态的开始阶段，体重只传递到跟骨区域，从而在跟骨区产生很高的峰值压强值，过大的足底压强极易对足底造成伤害，因而必须防止高压强区的出现，并且可以认为压强值越小，足底感觉越舒适。

观察其中一双鞋的足底峰值压强在一次实验中的变化，从实验开始至结束的60min内每5min取一次数值，用后一次的数值减去前一次的就可以得到足底峰压强的变化值，观察变化值可以看出不同阶段足底不同区域里的变化，如图5-44所示，红色区域是正值即表示随时间增加峰压强在增大，蓝色区域是负值即表示随时间增加峰压强在减少，且颜色越深绝对值越大。

刚开始的5min，第一～第五趾骨、足跟外侧足底压强减少，第二～第五跖骨、足跟内侧压强值增加，尤其是足跟内侧增加比较多;整体来看，足的前半部分内侧大多是在减少，而足的后半部分内侧是在增加，外侧是在减少，足的中间部分基本上都是增加的。

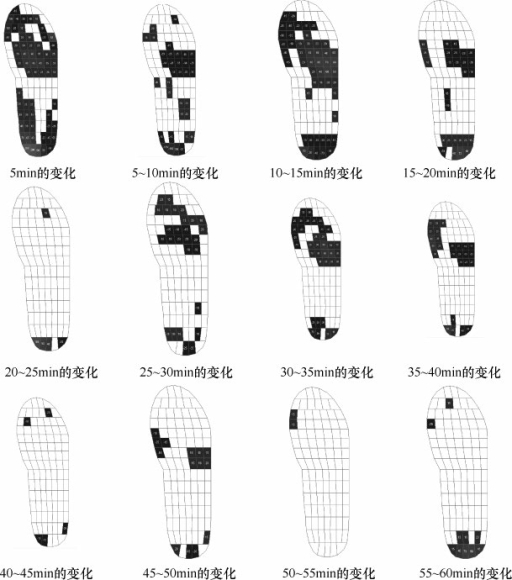
图5-44　足底压强的变化值

在第5～10min，第二趾骨压强减少了一点，第一跖骨压强值在增加，而第二～第五跖骨部分压强值都在减少，足弓部分压强值没有减少，足跟内侧在减少，而足跟外侧压强值则增加;总体看起来，足的前半部变化不太大，足的后半部分——足跟内侧减少得较多，足的中间部分大多是在减少。

在第10～15min，第一跖骨、第一趾骨以及足跟外侧压强值在减少，而第二～第五跖骨以及足弓外侧部位的足底压强值都在增大。整体看来，足的前半部分内侧压强值减少，足的后半部分外侧压强值减少，中间偏外侧的压强值增加。

在第15～20min，第二～第五跖骨部分压强值在减少，足跟外侧部分压强值增大，整体变化不大。

在第20～25min，足底压强值基本上没什么变化，足跟内侧小范围在增加，外侧小范围减少。

在第25～30min，第一～第五趾骨压强值增加，第二～第五跖骨压强值在减少，足跟内侧增加，足跟外侧减少;整体上来看，足的前半部分在增加，后半部分的内侧在增加、外侧在减少，中间部分稍许减少了一些，变化值都不大。

在第30～35min，第一趾骨、第一跖骨以及足跟内侧压强值都减少了，而第二～第五跖骨以及足跟外侧压强值在增加，足弓部分没有变化。整体看来，除了中间部分没变化，足的内侧值基本都是减少，外侧是增大的。

在第35～40min，第一跖骨部分以及足跟内侧的后半部分压强之都在增大，第二～第五跖骨以及足跟外侧的后半部分压强值在减少;整体上看，除了中间部分没有什么变化，足的内侧压强值增大而外侧减少。

在第40～45min，足底压强值基本无变化，只有第二趾骨以及足跟部分压强值在减少。

在第45～50min，足底压强值变化也不太大，第一跖骨附近压强值在减少，第四～第五跖骨压强值增加，足跟部分也有少许变化，其他部位没有变化。

在第50～55min，足底压强值几乎无变化，稍许的变化发生在足的前半部分的内侧，即第一趾骨和跖骨的内侧，压强值稍微增大了一点。

第60min，除第一跖骨部位足底压强值稍微减少了一点，第一趾骨以及足跟部都是在增大的，但是整体还是保持稳定的。

如图5-45所示，随时间增长，软底鞋和中等硬底鞋都呈缓慢增长的趋势，而硬底鞋开始值比较高，5min后迅速下降，后来的时间里基本没有什么大的变化。由于穿鞋后足弓塌陷，因此造成足底压强增大。总体来看，硬底鞋大于中等硬底鞋大于软底鞋。

软底鞋的趋势方程为:

y=-0.0237x6+1.0575x5-18.36x4+155.37x3-657.4x2+1269.5x+300.96，拟合优度R2=0.6463

中等硬底鞋的趋势方程为:

y=-0.0072x6+0.2889x5-4.4242x4+32.28x3-114.92x2+194.5x+276.73，拟合优度R2=0.674

硬底鞋的趋势方程为:

y=0.0026x6-0.12x5+2.2105x4-20.17x3+93.068x2-190.81x+370.33，拟合优度R2=0.8058

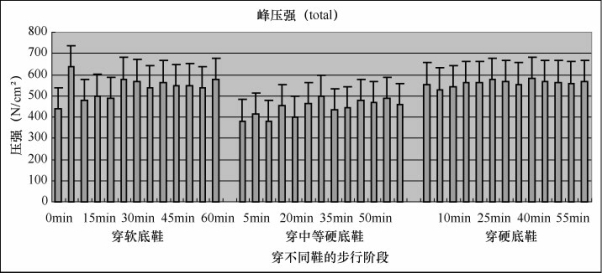
图5-45　穿不同鞋步行阶段的足底压强图

由趋势方程也可以看出，三双鞋的足底压强依时间变化呈现上升趋势，并且硬底鞋的要高于其他两双。

(三)穿不同鞋的足底分区的面积

长时间步行后由于足弓承受不了长时间的负荷，足底的肌肉开始发挥代偿性作用，接触面积发生改变。

测试结果表明，软底鞋的第一跖骨头的负重比例约占全部跖骨头的38.79%，中等硬底鞋的第一跖骨头的负重比例约占全部跖骨头的42.88%，而硬底鞋的第一跖骨头的负重比例约占全部跖骨头的37.63%。

如图5-46所示，软底鞋和中等硬底鞋接触面积差不多大，硬底鞋因为鞋底最硬接触面积也最小，最软的鞋(软底鞋)在10min内有所升高之后和中等硬底鞋都基本没有变化，硬底鞋随时间增长呈现“升高—下降”的趋势。

总体来看，接触面积呈现如下规律——软底鞋大于中等硬底鞋，中等硬底鞋大于硬底鞋。

图5-46　穿不同鞋步行阶段足底接触面积图

(四)穿不同鞋的足底分区的冲量

冲量可以表明力在一定时间内对足底各区域连续作用所产生的累积效应。足底各区域冲量的大小受每个区域的压力值和接触时间两个因素的影响。足底冲量可表明足底各区分载负荷比例，也可以推知足底各区域对地面施力的相对大小。当足与地面接触过程中应注意足底压力和作用时间的关系;应充分利于足弓等的减震功能，增加足与地面的接触时间，减小冲击力值，避免运动损伤。

如图5-47所示，软底鞋和中等硬底鞋开始的冲量都比较小，随时间增长而加大，到20min后基本保持稳定，硬底鞋开始冲量值就比较大，之后的一小时内基本保持稳定。总体来看，冲量呈现如下规律——硬底鞋大于软底鞋，软底鞋大于中等硬底鞋。

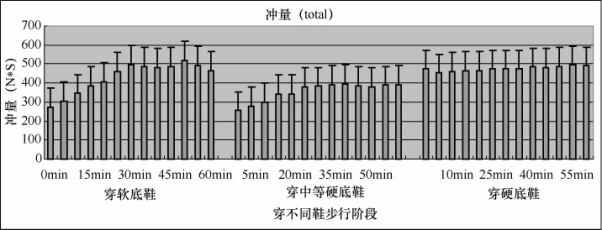
图5-47　穿不同鞋步行阶段足底冲量图

(五)穿不同鞋行走过程中的压力中心变化

三双不同鞋的开始时刻到60min的足底压力中心曲线(图中用红色线标出)，如图5-48所示。

图5-48　穿不同鞋行走足底压力中心曲线的变化

压力中心移动曲线两头应尽量平直，增加稳定性，且避免崴脚、磨脚。压力中心的变化与下肢关节周围肌肉的变化及整个身体重心运动相关联。每只脚的压力中心曲线直接反映了踝关节肌肉的神经控制，脚底屈肌、伸肌可以调整身体的压力中心。压力中心轨迹揭示足运动稳定性。

刚开始的5min，足底压力中心的长度就表现为软底鞋最长，压力中心移动曲线长且靠前，足底压力中心在足跟着地后逐渐移到第二跖骨，最舒适;在第60min时有折返且长度进一步变短;中等硬底鞋的压力中心曲线的长度缩短最少;硬底鞋的压力中心曲线的长度缩短最大，走到最后最不舒适。

(六)穿不同鞋对足的内外翻影响

由图5-49、图5-50可知，软底鞋内侧增加，外侧降低，所以是内侧力量偏大，提示足弓有塌陷趋势，容易引起外翻。并且硬底鞋内侧降低，外侧增加，所以是外侧力量偏大，容易引起内翻。

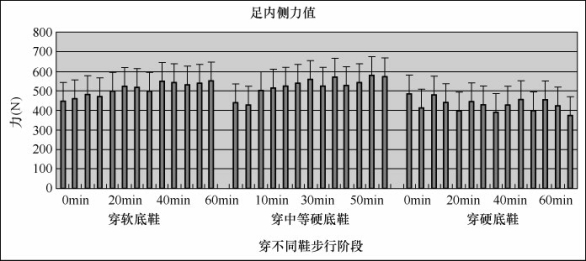
图5-49　受试者穿不同鞋步行阶段内侧足的最大力值

图5-50　受试者穿不同鞋步行阶段外侧足的最大力值