1.机械特性的物理表达式

电动机的电磁转矩物理表达式为

式中 C_M1——折算到定子边的异步电动机的转矩常数

Φ_m——基波磁场的每极磁通；

I′₂——转子电流的折算值；

cosφ₂——转子回路的功率因数。

此式的推导从物理概念出发，与根据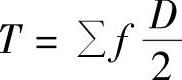而推导出来的电磁转矩公式完全相同，故称式（2-13）为异步电动机机械特性的物理表达式。

物理表达式反映了异步电动机电磁转矩产生的物理本质，异步电动机的电磁转矩是由主磁通Φ_m与转子电流的有功分量I′₂cosφ₂相互作用产生的，在形式上与直流电动机的转矩表达式相似，它是电磁力定律在异步电动机中的具体表现。

2.机械特性的参数表达式

由电动机的等效电路，我们得出电动机的电磁转矩T的参数表达式为

式（2-14）是由异步电动机的电源电压U₁、频率f₁、电动机的参数（r₁，r′₂、x′_1σ、x_2σ、p及m₁）以及转差率s来表示的，所以称为机械特性的参数表达式。显然，当U₁、f₁及电动机的参数不变时，电磁转矩T仅与转差率s有关，令s在-∞＜s＜+∞之间变化，由式（2-14）算出不同s所对应的T值，从而画出了T=f（s）曲线，如图2-16所示。通过s和n之间的关系，经过简单的坐标变换，上述的T=f（s）曲线即为异步电动机的机械特性n=f（T）。

在图2-16中，当电磁转矩达最大值T_m时所对应的转差率s_m称为临界转差率。

图2-16 三相异步电动机的机械特性

临界转差率表达式为

将s_m代入式（2-15）即得最大转矩为

正号表示异步电动机处于第一象限电动状态，负号则适用于第二象限发电状态。

在一般异步电动机中，通常r₁<<（x_1σ+x′_2σ），为此，上两式又可近似为

同样，其中“+”号用于电动状态，“-”号用于发电状态。由式（2-16）和式（2-17）可知，电动状态与发电状态s_m相同，但是由于r₁的存在，使发电状态的|T_m|比电动状态的T_m大些。如果忽略r₁的影响，电动状态与发电状态的|T_m|相等。在以后的分析计算中，为简单起见，都认为电动状态与发电状态的T_m相等。

T_m是异步电动机可能产生的最大转矩，为使电动机在运行中不会因短时过载而停机，要求其额定转矩T_N小于T_m，使电动机具有一定的过载能力。我们称最大转矩T_m与额定转矩T_N之比为过载倍数，或过载能力，用λ_M表示，即λ_M=T_m/T_N。λ_M是异步电动机的一个重要指标，一般异步电动机的λ_M=1.6～2.2。

由转矩公式可知，最大转矩主要与下述因素有关：

（1）在电源频率及电动机参数不变的情况下，最大转矩与定子相电压平方成正比，而临界转差率与U₁无关，保持不变；(www.daowen.com)

（2）当U₁、f₁及其他参数不变而仅改变转子回路电阻r₂′时，最大转矩不变而临界转差率改变，它与r′₂成正比；

（3）当U₁、f₁及其他参数不变而仅改变（x_1σ+x′_2σ）时，s_m和T_m都近似与（x_1σ+x′_2σ）成反比。

在电动机起动时，将s=1代入式（2-14）即得异步电动机起动转矩的参数表达式为

由式（2-18）可知，起动转矩也与电源电压U₁平方成正比。

异步电动机在额定电压，额定频率及电动机固有的参数条件下，可以得到其固有的起动转矩T_Q，它与额定转矩的比值，称为异步电动机的起动转矩倍数，用K_M表示，即K_M=T_Q/T_N，一般要求K_M＞1，这样电动机才能带动额定负载顺利起动。

三相异步电动机机械特性的参数表达式常用来分析电动机的电压、频率以及结构参数对机械特性的影响。

3.机械特性的实用表达式

利用机械特性的参数表达式计算三相异步电动机的机械特性时，需要知道电动机的绕组参数，计算比较复杂，在产品目录中有些参数用户也查不到，只有通过实验才能得到。如果能利用电动机的铭牌数据和相关手册提供的额定值进行计算，就比较实用和方便了。异步电动机机械特性的实用表达式为

式（2-19）使用起来方便实用，故称为机械特性的实用表达式。式中T_m及s_m，可用下述方法求出：

T_m=λ_MT_N （2-20）

T_N=9550P_N/n_N （2-21）

式中，P_N单位为kW，n_N单位为r/min，T单位为Nm。将T=T_N，s=s_N代入式（2-17）可得

为此，只要从电动机产品目录中查出该电动机的P_N、n_N、λ_M。由式（2-20）至式（2_-22）算出T_m及s_m，然后代入式（2-19），即得该电动机的机械特性实用表达式。

当三相异步电动机在额定负载范围内运行时，转差率很小，额定转差率s_N仅为0.015～0.05。由图2-16知，当s=s_m时，机械特性为直线段，而当s=s_m时，，则式（2-19）可简化为

这就是机械特性直线段的表达式，又称机械特性的直线表达式，具有与他励直流电动机相似的特性。式中T_m=λ_MT_N的计算方法仍由式（2-20）求出；至于s_m，应用新的公式计算。把T=T_N，s=s_N代入式（2-20），可以求得

s_m=2λ_Ms_N （2-24）

直线表达式（2-24）用起来更为简单方便，但是必须注意两点：

（1）此公式只能用于运行点处于机械特性的直线段或s=s_m的情况下。如果不能确定运行点处于直线段，则只能使用实用表达式或参数表达式；

（2）直线表达式中的s_m必须采用s_m=2λ_Ms_N求取，而不能用式（2-22）来计算。