异步电动机的工作特性是指在额定电压、额定频率、额定接法及定转子回路不外接阻抗的情况下，电动机的转速n、定子电流I₁、电磁转矩T、功率因数cosφ₁及效率η，从空载到额定负载的范围内，与输出功率的关系。异步电动机的工作特性可以用计算方法获得。在已知等效电路各参数、机械损耗、附加损耗的情况下，可以由计算得到n、I₁、T、cosφ₁、η，从而得到电动机的工作特性。对于已制成的异步电动机，其工作特性也可以通过试验求得。中、小型电动机，用测功机作为负载测取不同转速下的输出转矩T₂，同时测取I₁、cosφ₁，从而可算出P₂、η，也可得到工作特性。而对于大容量异步电动机因受到设备的限制，通常是由空载和短路试验测出电动机的参数，然后再利用等效电路来计算出工作特性。

1.转速特性

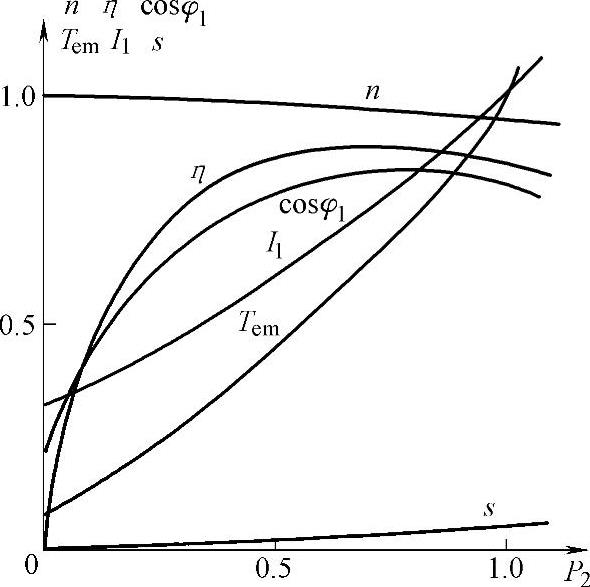
图2-15 异步电动机的工作特性

转速特性如图2-15所示的n曲线和s曲线。可以看出，当P₂=0空载时，n≈n₁，s≈0。而当输出功率P₂=T₂Ω增加时，负载转矩T₂增大，为使电磁转矩与负载转矩平衡，转子电流要增大，因此转子对气隙磁场的相对切割速度Δn=n₁-n=s_n1必须增加，即转差率s的曲线要随P₂增加而增加，与之相对应，转速n的曲线呈下降趋势。一般异步电动机额定运行时的转差率很小，控制在0.015～0.05之间，从空载到满载时，转速从n₁降到n_N=（1-s_N）n₁=（0.985～0.95）n₁，变化不大。所以转速特性n=f（P₂）下降的程度不大，类似于并励直流电动机的特性。

2.定子电流特性

电动机的定子电流I₁=I_m+（-I₂）。空载时，I₁≈I_m，随着负载P₂的增加，s增大，I₂′增加，使与之相平衡的定子电流中的负载分量增加。因此，I₁几乎随P₂成正比地增加。定子电流的特性曲线如图2-15中I₁曲线所示。

3.电磁转矩特性T=f（P₂）

电动机电磁转矩T=T₂+T₀。电动机从空载到满载，其转速n及主磁通Φ_m基本不变，所以其机械损耗P_Ω及附加损耗P_s基本不变，固而空载转矩T₀也基本不变。由于输出转矩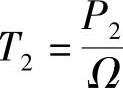近似于随P₂成正比地增加。所以T=f（P₂）近似于上升的直线。(www.daowen.com)

4.定子功率因数特性

从电动机的等效电路可以看出，异步电动机是一个感性电路，因此异步电动机其功率因数永远小于1，且为滞后。空载时，I≈I_m，基本上是无功电流，所以cosφ₁₀＜0.2，很低。当负载增加时，定子电流的有功分量增加，所以cosφ₁增加。一般电动机都设计成在额定负载时cosφ_N最高。超过额定负载时，当P₂继续增大时，转差s变大，使转子回路的阻抗角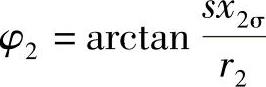变大，cosφ₂下降，从而使cosφ₁又重新降低，如图2-15中cosφ₁曲线所示。

5.效率特性η=f（P₂）

根据异步电动机的效率公式

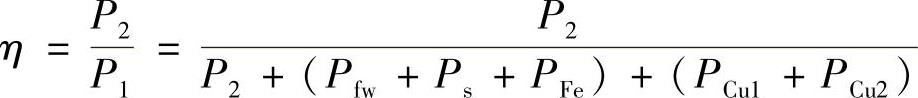
画出其特性曲线如图2.3-6的η曲线所示。从空载到满载运行过程中，由于主磁通变化很小，故铁损耗认为不变；在此区间转速变化很小，故机械损耗也认为不变。因此（P_fw+P_s+P_Fe）可视为不变，称为不变损耗，而定、转子铜损耗与各自电流的平方成正比，即（P_Cu1+P_Cu2）是随负载P₂而变的，称为可变损耗。当P₂=0空载时，显然η=0；当P₂开始增加时，η表达式的分子比分母增长快，所以效率升高；当负载加大到使可变损耗等于不变损耗时，效率最高。一般电动机通常设计成额定负载P_N时效率接近最高。若负载再增加，由于（P_Cu1+P_Cu2）与电流平方成正比增加，η表达式的分母比分子增长快，使效率反而降低。

由于异步电动机cosφ₁及η都在额定负载附近达最大值。所以电动机的容量选择，应尽可能地使之在其额定状态下运行，而不宜在空载或轻载状态下长期运行，出现“大马拉小车”的现象。否则，cosφ₁及η都很低，不利于节能降耗。