8．4．3．1　基于恒功率控制的电流源型虚拟同步发电机

2005年，荷兰代尔夫特科技大学的J．Morren在研究风机的最大功率跟踪控制时，为增加分布式发电对电网频率变化的惯性响应，在风机参考转矩的基础上加入因电网频率变化产生的附加转矩，即虚拟的惯量和阻尼，使得以风机为代表的分布式电源能够参与电网频率调节，提高电网稳定性。2007年，以荷兰代尔夫特科技大学为主导机构之一的欧盟VSYNC计划首先提出了VSG的概念，该计划旨在通过增加分布式发电对电网频率的惯性响应来提高电网的稳定性，并将之前应用于风机的成果推广至基于储能装置的分布式电源结构中。

VSYNC提出的VSG结构中的储能装置不仅可平抑新能源的出力波动，还能够为抑制电网频率波动提供额外的功率补充。一般来说，储能变流器工作在如图8-16所示的恒功率控制之下，VSG控制在原有有功功率参考的基础上，根据频率变化动态调节有功功率指令：

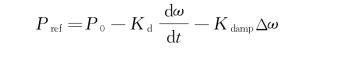
式中，P0代表有功参考值，Δω为电网角频率与额定角频率之间的差值；Kd和Kdamp分别体现了频率变化时的虚拟惯量和阻尼；Pref为考虑频率变化之后的电力电子变流器的有功功率指令。

该控制方式借鉴了同步发电机二阶模型中转子的转动惯量以及阻尼线圈的阻尼效应。然而，基于恒功率控制的VSG与具有电压源特性的同步发电机仍然具有较大差别，前者本质上还是跟踪电网相位的受控电流源，没有摆脱锁相环的限制，不能工作于弱电网或微网孤岛等不具备稳定电压参考的工况下。

8．4．3．2　具有电压源特性的虚拟同步发电机控制

电压源型VSG 控制组成结构如图8-20所示，该结构模拟了同步发电机现实中的工作方式，摆脱了锁相环的限制。图中的转子机械方程为：

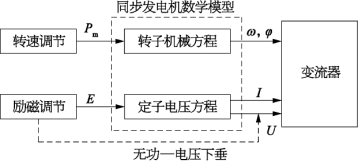
图8-20　电压源型虚拟同步机控制组成结构(www.daowen.com)

φ为abc dq坐标系转换角度

式中：J为转子的转动惯量；ω为极对数为1的情况下的电气角频率；ωg为同步角频率；Tm和Te分别为同步发电机的机械转矩和电磁转矩；Pm和Pe分别为对应的原动力机械功率和电磁功率；D为阻尼系数。

图8-21　同步发电机定子等值电路

同步发电机定子等值电路如图8-21所示，其电压方程为：

式中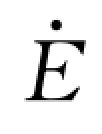：为励磁电流在IEF定子线圈上产生的空载感应电动势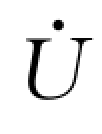；和分别为机端电压和定子电流；x和r为同步电抗和定子绕组电阻，通常情况下x远大于r。近年来出现的电压源特性的VSG普遍借鉴了转子机械方程，对励磁系统的模拟程度不同，派生出不同的电压型VSG结构，下面对其简要介绍。

如果将励磁系统和定子电压方程统一考虑，可用无功功率一机端电压这一下垂曲线来体现自动调节励磁装置在机端电压上的整体调节作用。此时的有功功率可表示为：

式中：Ug为电网母线电压；δ代表机端电压与电网母线电压之间的相角差；xΣ表示机端与电网之间的线路电抗与变压器电抗之和。这种控制方式的特点是结构简单，无需模拟励磁系统，直接为变流器提供电压参考值。