6．1．2．1　电力系统稳定器的由来及原理

由于电力系统的发展、互联电力系统的出现和扩大、快速自动励磁调节器和快速励磁系统的应用，国内外不少电力系统出现了低频功率振荡，严重影响电力系统的安全稳定运行，成为制约联络线输送功率极限提高的最重要因素之一。

20世纪50年代，苏联在建设古比雪夫莫斯科输电系统时就发现，当线路输电功率达到某一定值后，系统就会在没有任何明显的扰动下也出现增幅振荡。这种现象被称为“自发振荡”，其实质就是今天所说的低频振荡，当时研制的“强力式励磁调节器”解决了这个问题，在实际电力系统中得到了应用。

为了抑制低频振荡，人们不断研究探索，研制了以发电机功率、发电机组的轴速度、发电机机端电压频率为信号的附加励磁控制装置，称为电力系统稳定器（power system stabilizer，PSS）。由于PSS具有物理概念明确、参数易于选择、电路简单、调试方便等优点，已为各国电力系统普遍接受和采用。

PSS是一个附加励磁控制装置，其作用是提高电力系统对机电振荡模式的阻尼，以抑制自发低频振荡的发生，减小系统中由负荷波动引起的联络线功率波动，加速功率振荡的衰减，因而有效地提高电力系统的稳定性。

在一定的电力系统运行条件下（例如远距离、重负荷等），自动电压调节器产生的阻尼力矩分量与转速变化反方向，因而是负阻尼力矩分量；当自动电压调节器的负阻尼分量超过发电机的固有正阻尼分量时，就会发生低频振荡，电压调节器的负阻尼作用是产生低频振荡的根本原因。

图6-4　单机无穷大母线系统

PSS是通过电压调节器的调节作用而实现对低频振荡控制作用的。PSS的输入信号可以取自同步电机的电功率、电机的功角、轴速或它们的组合。下面通过飞利普斯-海佛容（Phillips-Heffrom）模型为例，结合图6-4、图6-5，说明PSS的原理和参数选择。

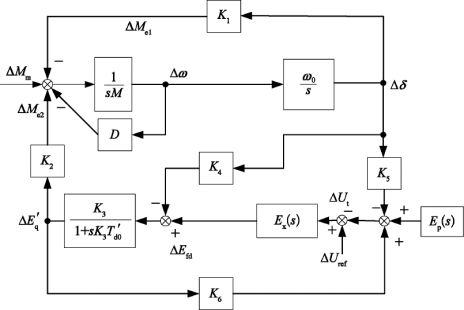
图6-5　单机无穷大母线系统模型

图6-5中，Ex（s）代表同步发电机的电压控制系统，Ep（s）代表电力系统稳定器，其输入为Δω，“－”表示以电功率负增量进行控制；

K1——假定d轴磁通为常数，由于转子角度的变化，而引起的电气转矩的变化；

K2——假定转子角度为常数，由于d轴磁通的变化，而引起的电气转矩的变化；

K3——阻抗因数；

K4——由于转子角度变化的去磁效应；

K5——假定d轴磁链的电压为常数，由于转子角度的变化，引起的发电机端子电压的变化；

K6——假定转子角度为常数，由于d轴磁链的变化，而引起的发电机端子电压的变化；

D——发电机阻尼系数。

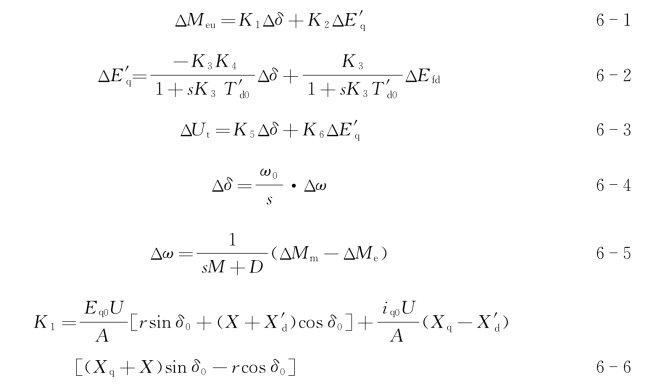
式中：Xd、Xq、X′d分别为发电机纵轴电抗、横轴电抗、纵轴暂态电抗，r、X分别为线路电阻和电抗，P0、Q0分别为发电机的有功功率、无功功率，Ut0、U分别为发电机端电压和无限大母线电压。

发电机工况（设Δδ）一旦变化，产生的电压变化为K5Δδ，经发电机电压调节器产生的力矩ΔMeu为

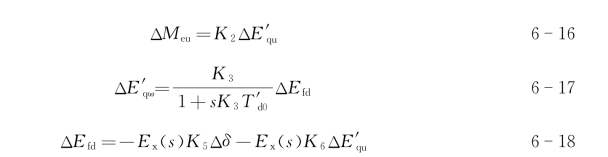
式中：“－”表示电压调节器按电压负增量调节，产生的电磁力矩为

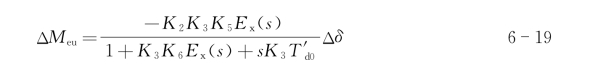
在研究低频振荡问题时，发电机之间仍保持同步运行，发电机内各机电量Δω、Δδ、ΔUt、ΔMe2、ΔEq、ΔEfd等可以认为按某一低频频率（一般为0．2～2．5 Hz）正弦振荡。这样，这些量都可以用正弦向量来表示，它们都可以在Δδ-Δω坐标平面上以向量表示，如图6- 6所示。

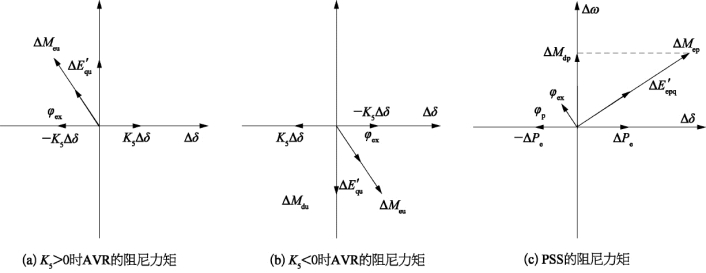
图6-6　AVR和PSS的阻尼力矩(www.daowen.com)

在Δδ-Δω坐标平面上，与Δδ正方向同向的力矩是正的同步力矩，与Δδ正方向反相的力矩是负的同步力矩；与Δω正方向同相的力矩是正的阻尼力矩，与Δω正方向反相的力矩是负的阻尼力矩。一般来说，通过励磁回路产生的电磁力矩ΔMeu不会正好在Δδ轴或Δω轴上。这时可以将它投影到Δδ轴和Δω轴上，ΔMeu在Δδ轴上的分量称为同步力矩分量，在Δω轴的分量称为阻尼力矩分量，如图6-6所示。

以低频振荡频率ωd代入式6-19，即令s＝jωd后就可以求得与Δδ相应的电磁力矩ΔMeu以及其同步力矩分量和阻尼力矩分量。

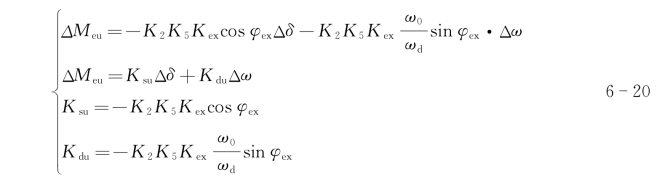
式中：Ksu、Kdu分别称为电压调节器产生的同步力矩系数和阻尼力矩系数，ω0＝314，ωd为振荡角频率，Kex、φex分别为

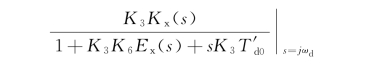
的模和角。

Kdu≤0时，电压调节器产生的阻尼作用为负阻尼作用；Kdu≥0，则为正阻尼作用。

Kex和φex系统参数（增益和时间常数）及系数K3、K6的函数，因此阻尼力矩系数K 也既是励磁控制系数的函数，又是同步电机运行工况（K2、K5、K6）的函数。

6．1．2．2　不同工况下同步电机模型系数的变化

在电力系统运行的同步电机，大多数的工作状态是固定的：一部分是作为同步发电机，主要向电力系统提供有功功率，根据电网要求，可以发出无功，也可吸收无功；一部分是作为同步调相机，主要用来调节电网电压，可以吸收电网无功，也可以向电网输出无功；还有一部分是作为同步电动机，主要从电网中吸收有功。

以图6-6所示的单机无穷大系统为例，计算了隐极转子同步电机和凸极电机两种情况下，同步电机有功从吸收1．0 pu到发出1．0 pu变化过程中，系数K1～K6的变化情况，计算时系统电压U 取0．98 pu，系统电抗X＝0．8。对每种电机又考虑了端电压为1．03 pu和0．95 pu两种情况。

以隐极式同步电机举例说明：

①K3与电机的工况无关，在由电动机状态到发电机状态的满负荷范围内，K3为常数。

②K3仅决定于电机参数和系统电抗。

③K6与同步电机的负荷有关，但在负荷大范围变化时，其变化也不大，同步电机有功绝对值增大时K6变小，且具有轴对称特性。

④K1有较大变化。有功为零时，K1不为零，有功开始增大时K1随着有功的增大而增大，在某一有功下达到最大值，此后，有功进一步增大时，K1将随有功的增大而减少。在所计算的有功范围内K1大于零。K1与有功的关系也具有轴对称特性。

⑤K2、K4在电机有功为零时均为零，同步电机工作于发电机状态时，K2、K4均为正，有功增大K2、K4也增大；当电机工作于电动机状态时，K2、K4都为负值，吸收的有功越大，K2、K4的绝对值也越大，具有原点对称性质。显然有乘积K2×K4＞0。

⑥K5在同步电机空载时也为零。在发电状态下，在输出有功增加时最初一段范围内（P＝0～0．25），K5也随之增大，符号为正，与有功相同。此后功率进一步增加时，K5减少，在到达某一临界值Pe时（Ui0＝1．03时，P0＝0．48；Ui0＝0．95时，P0＝0．54），K5变为零，功率进一步增加，K5变负，与有功符号相反，且越来越负。在电动机状态下工作时，情况相似，只是K5的符号正好相反。K5也具有原点对称性质，在吸收有功的最初一段范围内，K5为负并有最小值，与有功同号，以后K5逐渐变为零，吸收功率进一步增加时K5变正，与有功反号，且越来越大。

6．1．2．3　励磁控制系统参数对同步电机阻尼的影响

由式6-20可知，励磁控制系统参数对阻尼力矩系数Kdu的影响，表现在乘积Kexsinφex的大小和符号上。系数K3与同步电机的运行工况无关，K6则变化不大，因此Kex，φex主要取决于励磁控制系统参数（电压调节器及电机磁场回路参数），即开环增益和时间常数。

如果以一个快速励磁系统为例（时间常数为0．05 s），则Kex、φex、sinφex和乘积Kexsinφex与励磁控制系统开环增益Ka的关系曲线：

①Kex随着Ka的增大而增大。

②φex随着Ka的增大而减少，Ka＝1时，φex为－99°；Ka增大时，φex逐渐减少；Ka达到200时，φex只有－10°左右；Ka→∞时，φex→0。

③sinφex为负值，当开环增益Ka趋于无限大时，sinφex趋于零。对于现代大型同步电机，均配有快速电压调节器，因此在低频振荡的频率范围内，其滞后角φex一般为0～180°，sinφex基本上负值。

④乘积Kexsinφex在Ka从零开始增大的一段范围内（0～40），Ka增大，乘积Kexsinφex的绝对值也增大，阻尼力矩系数的绝对值｜Kdu｜也增大；Ka超过这个范围后增大时，Kexsinφex的绝对值反而减少，阻尼力矩系数的绝对值｜Kdu｜也减少；Ka→∞时，Kexsinφex→0，Kdu→0。

由此可见，在Ka变化时，自动电压调节器产生的阻尼作用，先是随着Ka的增大而增大，在某一临界值后，将随着Ka的增大而减少，Ka趋于无限大时，阻尼作用也趋于零。

6．1．2．4　同步电机运行工况对阻尼力矩系数Kdu的影响

从式6-20可知，运行工况对阻尼力矩系数的影响主要通过对系数K2、K5的影响表现出来。

当电机工作于发电机状态时，K2＞0，在小负荷情况下（P＜Pe时），K5＞0，因此有K2K5＞0，又因为Kexsinφex＜0，因此阻尼力矩系数Kdu＞0；在重负荷情况下，K5＜0，则有Kdu＜0，而且K2和K5的绝对值随着负荷的增大而增大，因此发电机负荷越重，Kdu越负。当电压调节器的负阻尼作用大于发电机的正阻尼因数时，合成阻尼为负，就会出现自发的低频功率振荡，这也就是低频振荡发生在重负荷弱联系情况下的原因。由于在发电机工作状态下，K2总是大于零，因此，电压调节器的阻尼作用可以通过系数K5的正负极大小来加以判断。K5＞0时为正阻尼作用，K5＜0时为负阻尼作用，K5的绝对值增大，其阻尼作用加大。同理，当电机工作于电动机状态时，也是在重负荷下容易发生低频功率振荡。