当电力系统负荷发生变化引起系统频率变化时，系统内并联运行机组的调速器会根据电力系统频率变化自动调节进入它所控制的原动机的动力元素，改变输入原动机的功率，使系统频率维持在某一数值运行，这就是电力系统频率的一次调整，也称为一次调频。

图3-1　电力系统一次调频和二次调频过程

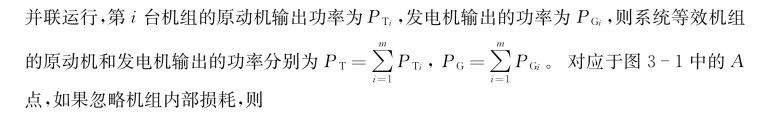
由于此时等效机组的输入和输出功率相等，系统将在A点运行。

如果电力系统负荷功率突然增加ΔPL系统负荷的静态频率特性曲线由PL（f）变为P′L（f）。由于电力系统中的电能是不能储存的，任何时刻电力系统中并联运行的机组发出的有功功率总和必须等于负荷所消耗的功率总和，所以，在电力系统负荷突然增加ΔPL的瞬间，系统等效机组的发电机必须立刻多发出有功功率ΔPL。等值机组发出的功率将从PGA突然增加到PGD，而等效机组的原动机输出仍然为PTA。数学表达式为

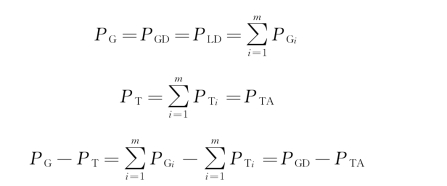
式中：PGD、PTA、PLD如图3-1所示。

根据能量守恒定律，为了保持系统等效发电机有功功率的平衡，机组会将转子中储存的一部分动能转换成电功率送往负荷，即有

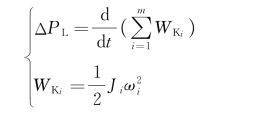(www.daowen.com)

式中　　WKi——系统中并联运行的第i台机组转子中储存的动能；

m——系统中并联运行机组的台数；

Ji，ωi——系统中第i台机组的机械转动惯量和机械角速度。

由上式不难看出，在等效机组释放转子动能的同时，机组自身的转速（频率）也随之下降。由图3-1可知，随着频率下降，一方面机组调速系统会按照等效机组的静态调节特性增加输入原动机的动力元素，使原动机输出功率增加；另一方面根据负荷的静态频率特性，负荷从系统取用的有功功率也要减少。上述过程一直进行到C点。在C点，f＝fC，等效机组的原动机输出功率与发电机输出功率相等，等于系统负荷的功率，等效机组处于稳定运行状态。此时的运行状态可用下列数学表达式描述

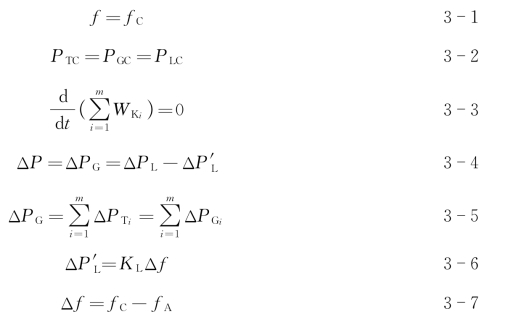
式中　ΔPG——等效机组多发出的有功功率；

ΔP′L——系统负荷从系统少取用的功率。

当电力系统负荷突然减少时，经过与增加负荷功率相反的调节过程以后，系统会在某一频率稳定运行，并同时满足式3-1～式3-7描述的各项内容，只是Δf和ΔP′L会变为正值，ΔPT、ΔPG会变成负值。

由图3-1可知，当负荷增加时，如果机组调速器不进行调节，即系统的等效机组的输入不变而仍为PTA，负荷增加的功率（ΔPL）全部由负荷频率调节效应调节。在这种情况下，系统将稳定在图中的B点，f＝fB，ΔfB＝fB－fA。图2-1中Δf1＝ΔfB－ΔfC就是一次调频的调节效果。

除了系统负荷固有的频率调整特性外，发电机组参与系统频率的一次调整具有以下特点。