Ramesh总结了自1917年以来泡孔长大模型的理论和实验分析^[39]。单泡孔长大模型是1917～1984年间大多数文献的研究重点，研究集中在被无限液体海包围的单泡孔由无限气体供应泡孔长大方面。实际上，泡孔是在实际有限的气体条件下随着无数泡孔互相紧靠而膨胀长大的。因此，工业上的实际需要促进了所谓的泡孔模型这一新模型在1984～1998年的建立。Amon和Denson^[40]于1984年提出了第一种泡孔模型，研究注射成型过程中一组被聚合物和溶解气体薄膜隔开的气泡的长大。自此，建立起两种泡孔模型：一种是封闭体系的泡孔模型，适用于注射成型；另一种是考虑了气体损失效应的改进型泡孔模型，适合于挤出工艺。所有资料在参考文献[39]中都有很好的总结。

1.无量纲泡孔长大模型^[40-43]

Arefmanesh等人建立了一种适用于注射成型的泡孔长大模型，适用于在没有气体损失的条件下大量紧密长大的泡孔。没有气体损失在注射成型中是恰当的假设^[41，42]，因为注射模具在注射全程中都是封闭的。这些研究结果与实验数据和理论预测值呈现出量上的吻合。该模型考虑了聚合物的黏弹性质，利用了质量和动量传递的同步方程。聚合物被看做是一个简单的Maxwell元件，有单一松弛时间常量。无量纲数在黏弹性液体中的泡孔长大模型中定义。许多论文都提出并使用了这一模型^[40-43]。这些方程也被用于微孔注射成型中预测泡孔长大，表示如下：

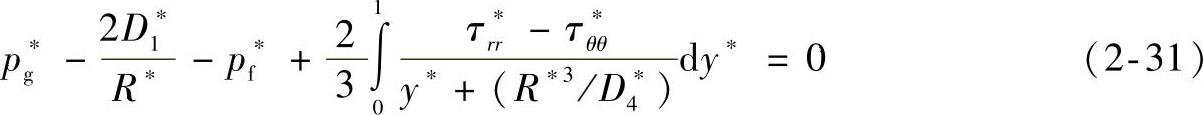
式中 p^∗_g——泡孔压力降；

p^∗_f——作用压力下降值；

R^∗——无量纲瞬时泡孔半径；

y^∗——减小的Lagrangian坐标（空间和时间坐标的结合）；

τ^∗_rr——径向的无量纲法向应力；

τ^∗_θθ——圆周方向的无量纲法向应力；

D^∗₁和D^∗₄——考虑了体系性能和加工条件的无量纲参数，是变量无量纲化过程中产生的，定义为

式中 S₀——泡孔长大的壳体半径（图9-7）；

p_a——大气压力；

R₀——初始泡孔半径；

σ_b——泡孔表面张力。

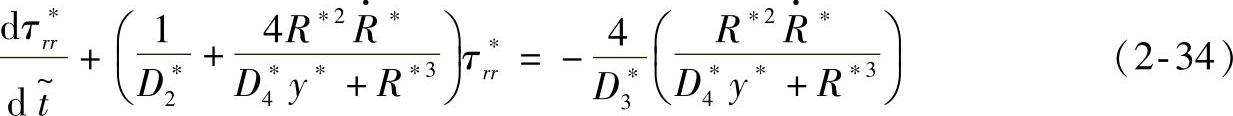
式中

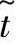——演算时间；

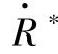——无量纲瞬时泡孔半径R^∗的时间导数。

D^∗₂和D^∗₃是无量纲参数，定义为

(www.daowen.com)

式中 λ——聚合物的松弛时间；

η_T——非牛顿气体-聚合物混合物的黏度。

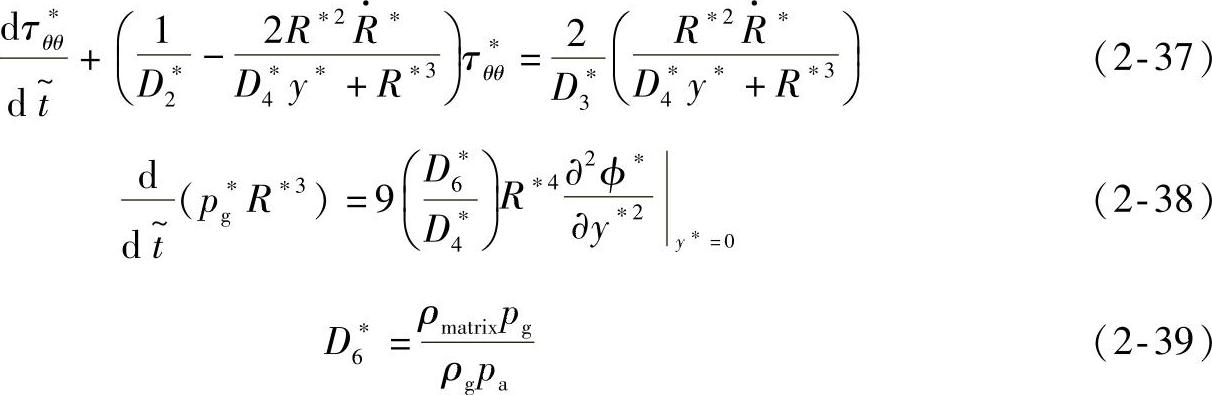
式中 ρ_matrix——气体-聚合物基体内的气体密度；

ρ_g——长大泡孔内的气体密度。

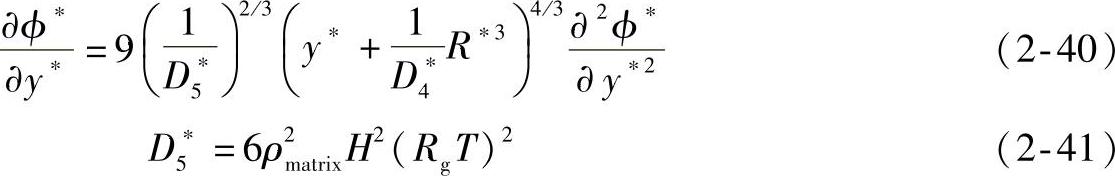
式中 H——Henry定律常数；

R_g——摩尔气体常数；

T——热力学温度；

ϕ^∗——气体浓度势函数的下降形式。

初始条件表示为

边界条件表示为

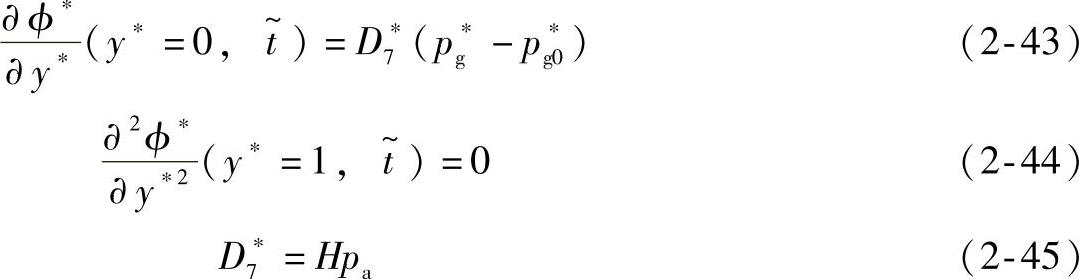
式（2-31）是动量平衡方程，与Maxwell黏弹性液体本构方程的分式（2-34）和分式（2-37）关联。式（2-38）表示整个泡孔界面的质量平衡。式（2-40）表示气体从气体-聚合物基体的外壳扩散到长大泡孔表面时的质量平衡^[40-45]。由于注射成型过程中模具闭合、注射速度快，所以其泡孔长大的边界条件可以通过假设气体没有损失而得以简化。

体系性能，如黏弹性、扩散性和基体密度等在模拟泡孔长大之前必须认真分析。气体与聚合物混合体系的黏度可参考第9章。此外，异相成核泡孔长大的初始泡孔半径将被简化，采用均相成核模型。通常，CO₂发泡PS时将0.1～1μm直径作为初始临界泡孔半径^[39]。尽管人们自1917年就开始研究泡孔长大模型，但描述实际加工过程仍然需要很多数据和理论完善。

2.快速预测最终泡孔尺寸的简单模型

已经建立了一个特别简单的模型用于注射成型，其有两个作用，一是描述初始泡孔长大，二是在注射过程结束后预测最终泡孔尺寸。尽管上述模型提供了通用方程，但仍然不是很适合于快速注射成型。

研究发现，气体累积在聚合物-填料界面时，在泡孔长大的初始阶段泡孔长大速度快于未填充体系。预测长大至一定程度的泡孔的尺寸（可能引起可见的表面缺陷）可以用于求出最短注射时间。在最短注射时间内，在表面长大的泡孔可能达不到使表面明显粗糙的可视尺寸。在注射成型中，填充与未填充聚合物体系的表面缺陷问题可以用第9章的初始泡孔长大模型来解释。

在三种条件下泡孔长大被终止：膨胀的泡孔长大材料完全充满模具；材料建立（冷却）起足够的刚性承受泡孔内气体的压力；不再有充足的气体持续供应泡孔发泡。这三个泡孔长大终止条件可用于理论模型或者泡孔长大计算的简化模型。