成核是一种物理现象，是新相形成的过程。成核可能源自自身结构调整，也可能源自外来“种子”，是释放外来变化诱发载荷的一种方式^{[29，30，31，32]}。微孔要么是均相成核，要么是异相成核。如果成核驱动力很高，那么活化能差就比均相成核和异相成核同时发生时的驱动力要小得多。发生这种情况的条件是气体在熔融聚合物中的过饱和度很大^[4]。Youn和Suh^[30]提出了一种热固性树脂成核模型。Colton和Suh^[31]总结了最常用的热塑性塑料成核模型，共有三种可能的成核模型。

1.均相成核理论

经典成核理论被广泛用作其他成核机理模型的研究基础，已被修正用于均相成核模型，其中考虑了自由体积效应^[31，32]。只有材料完全均质时均相成核才能发生，因为成核发生在泡孔成核所需活化能均匀的基材中^[4]。那么，均相成核的吉布斯自由能变化可以写为

ΔG_hom=-V_bΔp+A_bpγ_bp （2-12）

式中 ΔG_hom——均相成核的吉布斯自由能变化值；

V_b——泡核体积；

Δp——泡孔内的气体压力；

A_bp——泡孔表面积；

γ_bp——聚合物泡孔界面的表面能。

球形泡孔可以使剩余能量最小，实际上球形是不受剪切作用、理想成核的最佳泡孔形状。因此，除非另有说明，本章讨论的泡孔都是球形的。那么，如果γ_bp是各向同性的，式（2-12）就变为

ΔG_hom=-（4/3）πr³Δp+4πr²γ_bp （2-13）

式中 r——成核泡孔半径。

根据这一关系绘制出一幅重要的图，其给出了吉布斯自由能随半径r的变化情况。式（2-13）中的第二项是界面能，随r²增加，在图2-8中为上升曲线。式（2-13）中的第一项是体积吉布斯自由能，与r³Δp成正比，在图2-8中为下降曲线。吉布斯自由能ΔG（r）是r的函数，是界面能和体积吉布斯自由能的综合值。小泡孔的形成导致吉布斯自由能增加，直到成核泡孔半径大于临界尺寸为止。泡孔长大的临界尺寸与最大吉布斯自由能ΔG^∗（r^∗）有关。在dG/dr=0时可求出r^∗和ΔG^∗（r^∗）。此外，r=r^∗时，泡核与其周围环境处于不稳定状态，因为d²G/dr²＜0。如果r＜r^∗，体系就会通过将气体溶于聚合物中来降低其吉布斯自由能；如果r＞r^∗，泡孔长大就会导致吉布斯自由能下降^[30]。另外，如果泡孔尺寸大于临界泡孔尺寸r^∗，泡孔通常会变得稳定并长大。如果泡孔尺寸小于临界泡孔尺寸，那么泡坯就会塌陷。

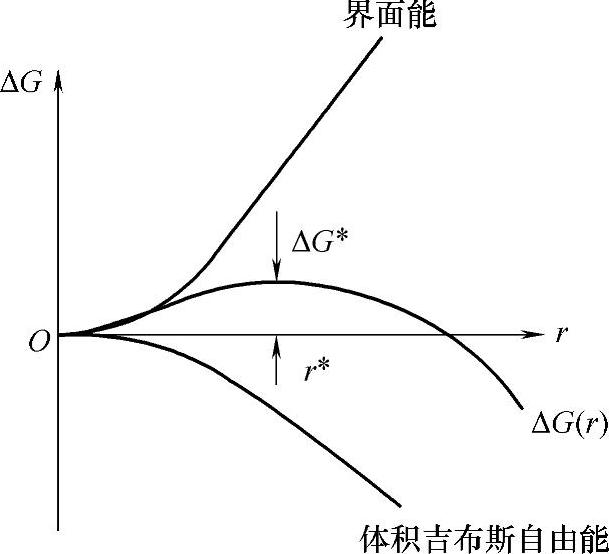
图2-8 吉布斯自由能变化与半径为r的球形泡孔均相成核间的关系^[29]（经过美国塑料工程师协会版权许可）

将式（2-13）微分可以求出临界泡孔半径r^∗，即

r^∗=2γ_bp/Δp （2-14）

还应该注意的是r^∗与成核速率无关。那么，临界泡核均相成核的吉布斯自由能由式（2-15）给出，即

式（2-15）适用于批处理发泡工艺，Δp（看做一级近似）是假定气体为理想气体时气体饱和聚合物的压力。然而，在注射成型中，Δp是瞬时注射压力，或者是整个注射行程中的平均注射压力。要掌握的重要一点是，无论是界面的表面能下降还是压力（批处理工艺中的饱和压力，注射成型中的注射压力）上升，吉布斯自由能都会下降，表现为成核速率提高，产生的泡孔数量增加。

根据聚合物中的每一种成分可以求出溶液的表面能。模拟方式有很多，其中之一是采用混合物法则，此法适用于低浓度助剂，如式（2-16）所示：

γ_s=γ_aw_a+γ_pw_p （2-16）

式中 γ_s——聚合物溶液的表面能；

γ_a——助剂的表面能；

γ_p——聚合物的表面能；

w_a——助剂的质量分数；

w_p——聚合物的质量分数。

如果将溶解的助剂加到聚合物溶液中，可以将γ_s带入前述的γ_bp方程中。Colton还利用自由体积变化对吉布斯自由能的影响来完善经典成核理论^[31]。聚合物的自由体积可以用很多方法来改变，如聚合物的热膨胀以及溶解气体和溶解助剂等成分。由于注射压力一般高达138MPa，即使是低黏度气体-聚合物混合物也是如此，因此与注射成型的压力相比，体积变化可以忽略。

活化能垒一旦确定，气泡的成核速率就可以计算出来。达到临界尺寸、形成稳定泡核的气束浓度C^∗通过假设Boltzmann分布给出，即

C^∗=C₀exp（-ΔG^∗_hom/kT） （2-17）

式中 C^∗——达到临界尺寸的气束浓度；

C₀——溶液中气体分子的浓度。

为了成核，必须克服能垒。一般来说，能垒取决于两个相互竞争的因素：①扩散进泡坯中的气体的能量；②形成泡孔表面所必须提供的表面能^[4]。一般来说，成核公式由下式给出^[4]：

dN/dt=N₀fexp（-ΔG/kT） （2-18）

式中 N——泡孔数量；

N₀——成核点的数量；

f——原子或分子格振动频率。

假设又有一个达到临界泡核的气体分子转变为稳定泡核，发生频率为f₀，则均相成核速率写为^[31]

N_hom=f₀C₀exp（-ΔG^∗_hom/kT） （2-19）

式中 f₀——均相成核的频率因子；

N_hom——均相成核速率。

有关微孔注射成型均相成核的数据很少。就成核所需能量值而言，即使是均相成核也并非是真正均匀的^[4]。表2-15列举了一些均相成核计算的参考数值^[31]。

2.异相成核理论

异相成核发生在成核所需能量较少的地方。成核能量需求低的地方是界面能量高的、不同材料之间的界面处。在实际注射成型中，大多数微孔注射成型实际上都是异相成核，因为塑料材料中含有多种添加剂，而且塑料本身也并不是一种纯的均相材料。此外，如果注射速度低或者压力降速率低，泡孔都不会同时成核。(www.daowen.com)

表2-15 均相成核计算的参考数值

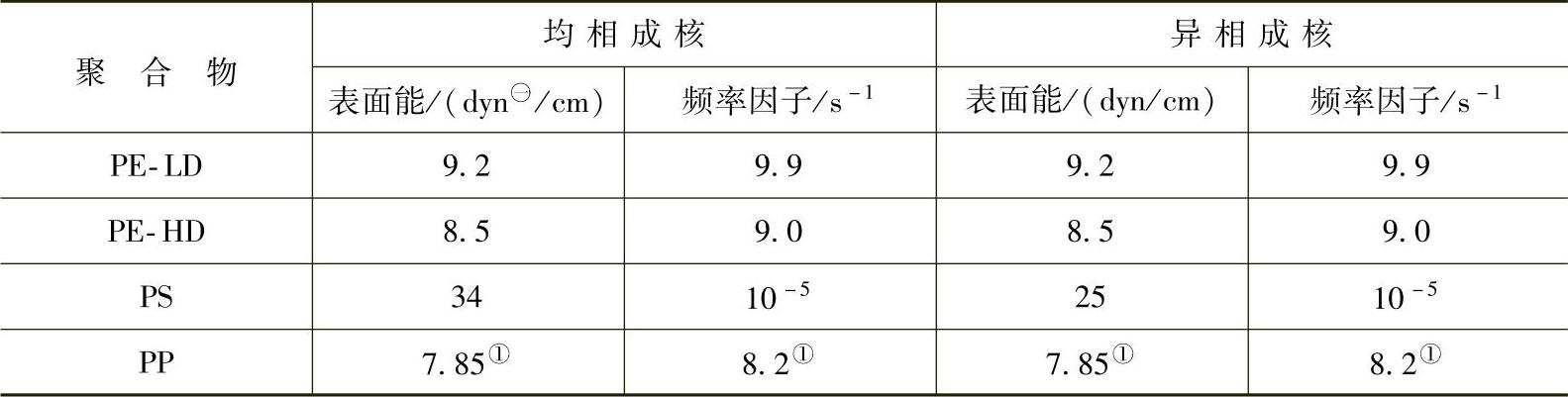
注：资料来源于Colton与Suh^[31]，经过美国塑料工程师协会许可。

①计算值。

㊀ 1dyn=10^-5N。——译者注

经典成核理论描述了两相界面第三相的异相成核^[31]。图2-9图示了气泡在聚合物和固体粒子界面处的成核。界面张力达到平衡^[31]，即

γ_ap=γ_bp+γ_abcosθ_w （2-20）

式中 γ_ap——固体粒子-聚合物的界面张力；

γ_bp——泡孔-聚合物的界面张力；

γ_ab——固体粒子-泡孔的界面张力；

θ_w——润湿角。

与式（2-12）相比，异相成核的吉布斯自由能变化可以写为^[31]

ΔG_het=-V_bΔp+A_bpγ_bp+A_abγ_ab-A_apγ_ap （2-21）

式中 ΔG_het——异相成核的吉布斯自由能变化；

A_ap——添加剂粒子-聚合物界面的表面积；

A_ab——添加剂粒子-泡孔界面的表面积。

根据式（2-13）中所作的类似假设和一些代数计算，式（2-21）可以写为

ΔG_het=[-（4/3）πr³Δp+4πr²γ_bp]S（θ_w） （2-22）

S（θ_w）=（1/4）[2+cos（θ_w）][1-cos（θ_w）]² （2-23）

S（θ_w）是聚合物、气体和辅助相粒子之间润湿角的函数，如图2-9所示。均相成核时S（θ_w）=1；异相成核时，S（θ_w）＜1^[4]。

将式（2-22）微分得到临界泡核半径（与临界泡核的平均半径相等）公式。与式（2-15）相比，临界ΔG_het变为

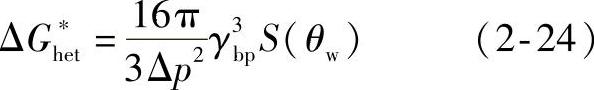
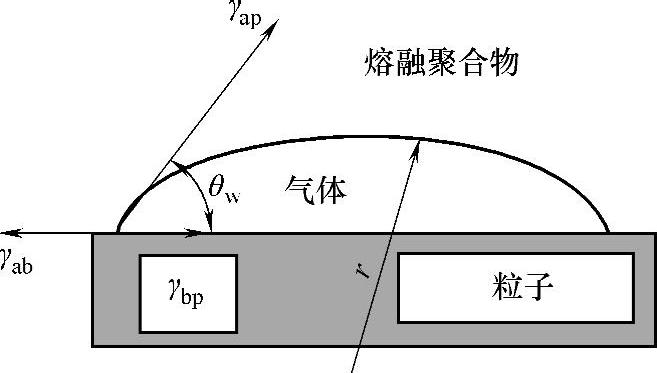
图2-9 聚合物-固体粒子界面处泡核的力平衡^[28]（美国塑料工程师协会版权许可）

Colton和Suh^[31]还指出，典型的润湿角约为20°，那么S（θ_w）约为10^-3。这就意味着界面的存在大大降低了异相成核的能垒，从而解释了为什么异相成核比均相成核要容易得多。换句话说，从成核的观点来看，最好选用填充材料。

异相成核速率与均相成核速率类似，由下式给出^[31]：

N_het=f₁C₁exp（-ΔG^∗_het/kT） （2-25）

式中 f₁——异相成核的频率因子；

N_het——异相成核速率；

C₁——异相成核点的浓度。

在参考文献[31]中，C₁=10¹⁰个成核点/cm³（粒子尺寸为0.1μm），硬脂酸锌粒子的γ_a≈24dyn/cm，异相成核时PS的γ_p=25.5dyn/cm^[31]。批处理时饱和压力的升高或者注射成型注射压力的升高以及成核点数量的增加都会提高成核效率，从而增加最终微孔注塑件的泡孔数量。

3.混合型成核理论

Colton和Sun^[31]在其论文中还讨论了混合型成核。均相和异相成核并不相互排斥。从能量的角度来说，异相成核一般更容易发生，因为异相成核的活化能垒低于均相成核。但是，材料中存在异相成核点处仍然可能发生一些均相成核。

异相成核也会影响均相成核，因为异相成核会减少固体粒子周边的气体，这一点易于理解。固体粒子周边的气体在热力学作用下会扩散进异相成核产生的泡孔中。此外，已有泡孔会吸收基材中更多的气体，因为气体扩散进更大的泡孔中也是因为受到热力学作用。因此，固体粒子附近的气体浓度C₀显著降低，可以按照一级近似模拟，即

C′₀=C₀-N_hetn_bt_b （2-26）

式中 C₀——混合型溶液中的气体分子浓度；

n_b——泡核中气体分子的数量；

t_b——第一次异相成核发生时开始计算的时间。

这样，将式（2-26）带入式（2-19）就能求出异相成核存在时的均相成核速率^[31]：

N′_hom=f₀C′₀exp（-ΔG^∗_hom/kT） （2-27）

根据式（2-25）和式（2-27）求出混合的均相成核和异相成核总的成核速率：

N=N′_hom+N_het （2-28）

Colton建议添加低于或接近于溶解度极限的可溶性助剂，在高压下将聚合物用气体饱和，制得微孔泡沫。