要制得微孔工艺所用的单相溶液，扩散速率是又一个需要理解的关键参数。对于连续发泡而言，扩散速率比溶解度要重要得多，因为气体计量必须在尽可能短的时间内完成。溶解度决定了可能的气体计量用量范围，见表2-13。如果溶解度是最大吸入量的静态测量值，那么扩散速率就是分子通过体系时与时间有关的运动或质量传递。因此，扩散速率决定了气体-熔融聚合物体系能否经济而又及时地完成这一工作。扩散速率是分子通过熔融聚合物的运动速率^[12]。扩散系数总是与某一温度下在特定熔融聚合物中运动的特定分子有关。扩散系数D_a按单位时间单位面积度量。表2-14为不同参考文献中给出的扩散系数D_a^[4，11-15]。

表2-14 估算的高温下气体在聚合物中的扩散系数D_a^[4，10-14] （单位：cm²/s）

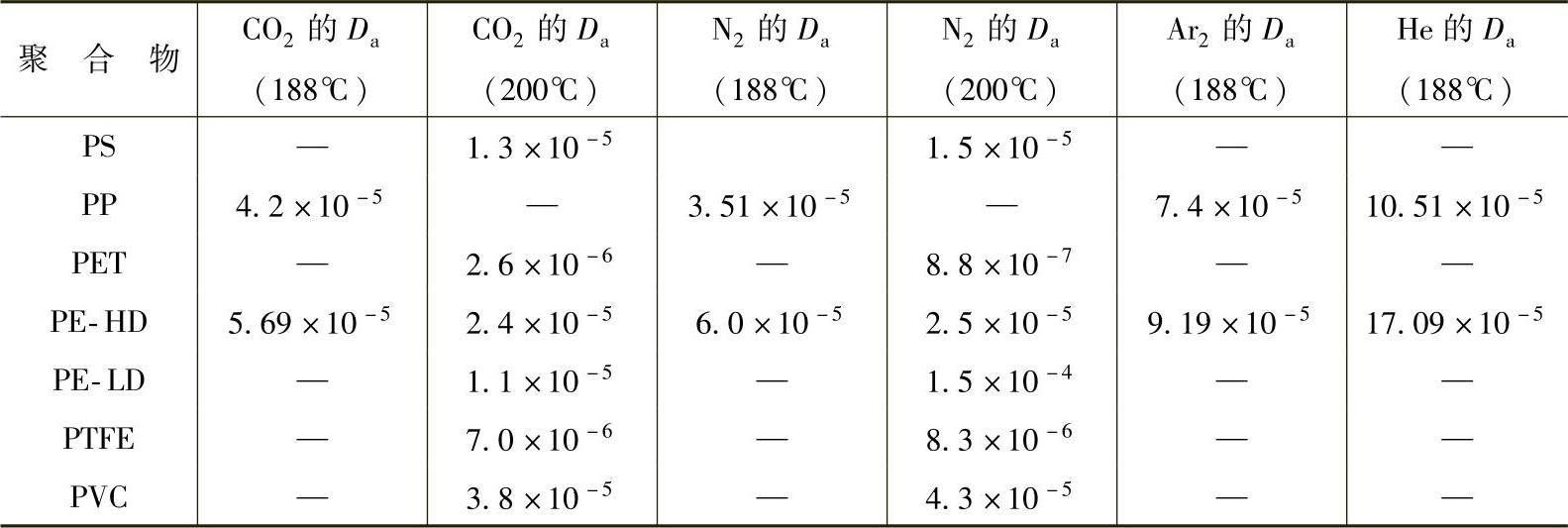
众所周知，室温下气体扩散很慢。估计CO₂在大多数热塑性塑料中的扩散速率为5×10^-8cm²/s。室温下N₂的扩散速率与CO₂基本相同。但在200℃的高温下这两种气体的扩散速率都比室温时高出3～4个数量级。在188～200℃、大气压力下，不受剪切作用时这两种气体在聚合物中的扩散系数估计在10^-4～10^-6cm²/s之间，见表2-14。选择加工条件时可根据这一数值进行定性估计或比较。但这一数值不是定量计算实际注射成型的有用数据，因为剪切会对表2-14中的数据产生很大的影响。

熔融塑料中气体扩散速率总的趋势是随着温度的升高而增大，与气体在塑料中溶解度的变化趋势相反。然而，参考文献中的数据表明，PE-HD中的气体扩散速率随着温度的升高而减小。对于CO₂来说，188℃时其在PE-HD中的扩散速率大约为5.7×10^-5cm²/s，而在200℃时则大约为2.4×10^-5cm²/s。N₂在HDPE中的扩散速率变化趋势与CO₂类似，188℃和200℃时分别为6.0×10^-5cm²/s和2.5×10^-5cm²/s。原因是结晶性塑料的复杂性可能对气体扩散过程产生很大的影响，引起结晶变化和温度变化。

气体小分子通过从自由区域迁移到自由体积区域在聚合物中运动^[12]。对于很多常用聚合物如PS、PE和PVC而言，扩散系数随着温度的变化并不明显。因此，上述常用聚合物的泡孔尺寸可能发生变化，但在聚合物经历瞬间温度变化时泡孔数量没有显著变化。另外，对少数聚合物来说，如聚对苯二甲酸乙二醇酯（PET）和聚乙烯醇（PVAL），在温度升至T_g以上时，扩散系数随着温度的升高而增大^[12]。

很多文献都讨论了气体在熔融聚合物中的扩散理论^[4，12]。假设在一定的高温下聚合物突然受到高压气体作用，通过气体扩散，聚合物接近于热力学平衡状态。驱动力是气体-聚合物体系的吉布斯自由能。扩散现象可以用偏微分方程表示^[4]：

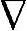（αC）=∂C/∂t_d （2-5）

式中 C——气体浓度；

α——气体扩散速率；

t_d——气体扩散时间。

扩散方程可以写为

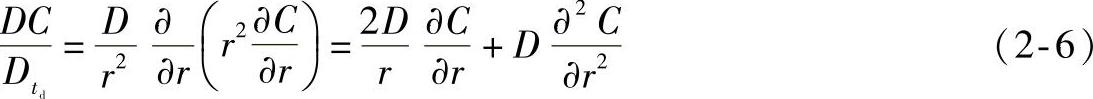
根据初始条件和边界条件，上式可以表示为

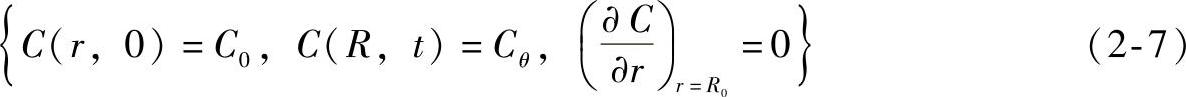
方程的解导出式（7-10），表明扩散系数与温度间的关系是Arrhenius关系，在Arrhenius关系中扩散速率随着温度的升高而提高，即

α～exp[-ΔG/（kT）] （2-8）

式中 ΔG——活化能；

k——Boltzmann常数；

T——热力学温度。

式（2-8）中的关系意味着扩散时间t_d与气体必须扩散进的塑料层的厚度平方成正比，如式（7-9）所示。气滴之间塑料层的厚度是扩散距离^[4]：(www.daowen.com)

式中 t_d——SCF扩散时间（s）；

l——气体扩散的熔体厚度（mm）；

α——气体（SCF）扩散速率[见式（7-10）]

表2-8给出了活化能ΔG的某一值。Throne^[12]建议采用扩散和渗透活化能比值的常数关系。对于某一种气体，如氮气，通过同系列的一系列聚合物这一比值可以看做常数，可以表示为

式中 E_p——通过聚合物p的扩散或渗透活化能。

在式（2-10）中，（g）表示未知气体，（N₂）是这里所用的已知气体。同样，如果某一气体在聚合物中的扩散或渗透活化能已知，那么常数比可以写为

式中 E_g——气体的扩散或渗透活化能；

p——已知聚合物；

p′——未知聚合物。

对于式（2-10）或式（2-11）来说，未知气体的扩散或渗透活化能可以根据已知气体或聚合物估算出来，只要聚合物属于同一系列即可。例如，如果CO₂和N₂在PE-HD中的扩散活化能分别为8.5kcal/mol和9.0kcal/mol，那么式（2-10）的比值就是0.94。根据表2-8，N₂在PS中的扩散活化能为10.1kcal/mol。根据式（2-10）的平均比值0.94估算出CO₂在PS中的扩散活化能大约为10.1×0.94=9.494kcal/mol，而表2-8中的测量值为8.7kcal/mol，估算误差约为9%。如果仅仅是为了估算，从工程上来说这一误差可以接受。如果某些活化能得不到，推荐用第9章的简单模拟程序获得。

扩散对微孔注射成型十分重要，因为它决定了其第一步是否成功。Throne^[12]总结了气体扩散的一般原则，与注射成型有关的如下：

1）增大聚合物侧基尺寸，气体扩散速率降低，但气体的扩散活化能随着侧基尺寸的增大而增加。

2）增加线形烯烃中甲基的数量会降低扩散速率，但使活化能增加，例如用苯作渗透剂的乙烯-丙烯共聚物中的情况就是如此。

3）高浓度极性基团降低扩散速率，但扩散活化能提高。

4）众所周知，提高结晶性材料的结晶度会降低气体在聚合物中的扩散速率。参考文献[12]对这一现象的物理解释是晶层的形成限制了扩散路径，使其更崎岖。扩散速率可能降低至原来的1/4或1/5。

单相溶液实际上是由完全扩散进熔融聚合物中的气体决定的。实际结果可能是气体分子占据了聚合物分子中的大部分空间。然而，还有很多微泡不在熔融聚合物的自由空间内，而是与熔融聚合物混合形成气体-聚合物混合物。只要这种混合物是均匀的，气体又没有形成大的气袋，那么这种气体-聚合物混合物在注射成型过程中就足以制备出微孔结构。只有这种气体与聚合物的混合物而并不是真正的单相溶液才能解释为什么气体只用6s，甚至不到6s的停留时间就能成功地计量注入熔融聚合物中进行混合和扩散（根据目前的理论，气体扩散形成单相溶液的理论最短时间为20s）^[26，27]。合理的解释是微孔注塑件是注射行程的短时间内注入喷嘴的气体经下方的静态混合器混合制备而成的^[6，7]。这是对这种动态工艺研究人员的挑战，也是工业技术走在学术研究前面的一个例子。人们有必要为采用气体扩散模型和必须符合实际加工条件的实验设备（而不是目前批处理加工所用的传统设备）建立新的或修正的理论。