为了定量地获得单叶片离心泵周期性动静干涉的非定常流动强度和湍流特性，本节根据文献[81]中的思想，在分析泵内部流动各速度分量之间关系的基础上，定义叶轮和蜗壳流道内的速度非定常强度系数和湍流强度系数。

与上节压力脉动一样，基于求解URANS方程，离心泵内部流动的速度量由两部分组成：时间平均速度分量和周期性速度分量，没有考虑与叶轮旋转周期频率无关的非定常流动现象中的速度随机波动分量。因此，相对速度分量和绝对速度分量可以由以下公式表达。

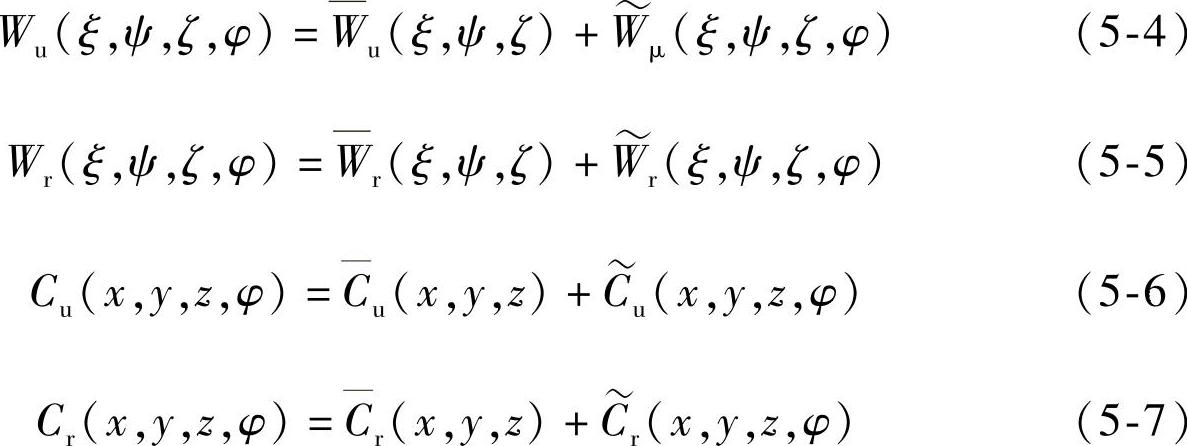
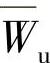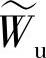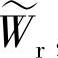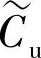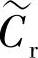式中，W_u代表相对速度的圆周速度分量；W_r代表相对速度的径向速度分量；C_u和C_r分别代表绝对速度的圆周速度分量和径向速度分量，其可以通过绝对速度在x和y方向上的分量，根据圆柱坐标系内不同方位角的关系进行求解得到本章此处主要考虑的是径向非定常动静干涉流动，即速度三角形内的绝对速度子午分量C_m近似等于径向分量C_r；、W_r、C_u和C_r分别代表以上各速度分量的时间平均形式，是考虑1个旋转周期内的平均值；，，和代表各速度分量的周期波动分量，是由于叶轮与蜗壳隔舌相对位置发生变化而产生的。离心泵典型速度三角形如图5-3所示。相对速度分量可由公式（5-8）和式（5-9）计算。

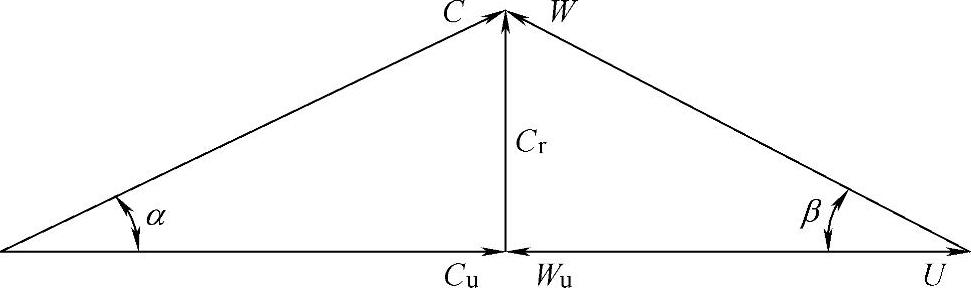
图5-3 离心泵典型速度三角形示意图[81]

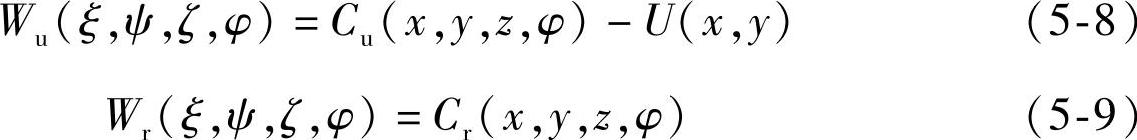
因此，时间平均速度分量可由下式计算。

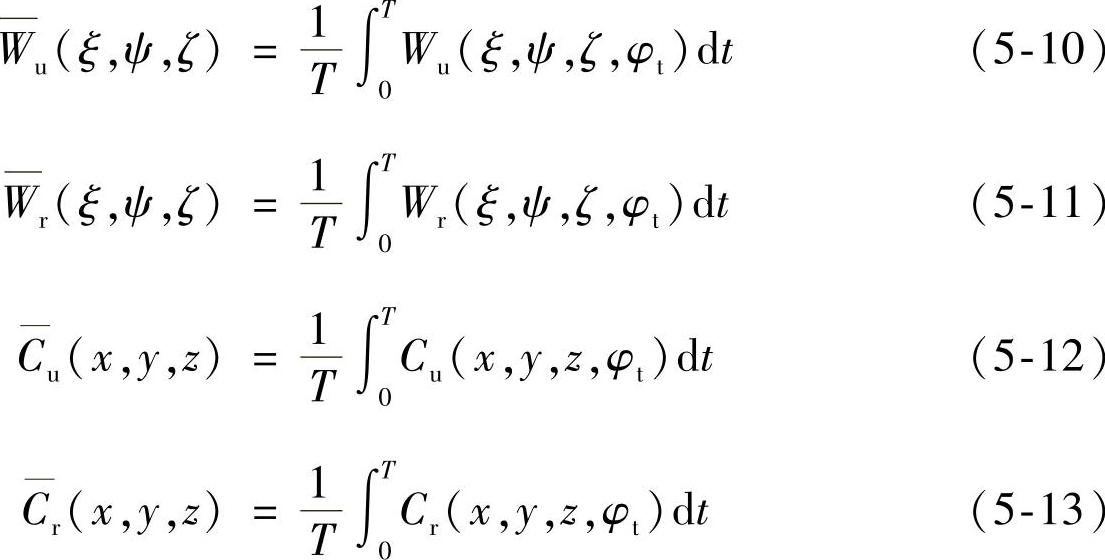
式中，φ_t是t时刻叶轮的转动位置；T是1个叶轮旋转周期。

为了定量地得到叶轮流道内相对流动的非定常特性，时变的叶轮非定常流动强度系数I_u可由方程（5-14）定义。I_u由2个方向上的周期性相对速度分量求均方根，并采用叶轮外径圆周速度u₂进行无因次化处理得到。因此，1个叶轮旋转周期内120个时间步长的时均相对速度非定常流动强度系数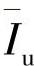可由公式（5-15）求得。由于公式采用的是相对速度分量，因此，该强度系数用于分析叶轮区域内旋转坐标系下的速度非定常强度，称为相对速度非定常强度系数。同理，绝对坐标系下的时变非定常流动强度系数S_u由公式（5-16）定义，考虑整个叶轮旋转周期的时均绝对速度非定常强度系数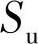由方程（5-17）定义。(www.daowen.com)

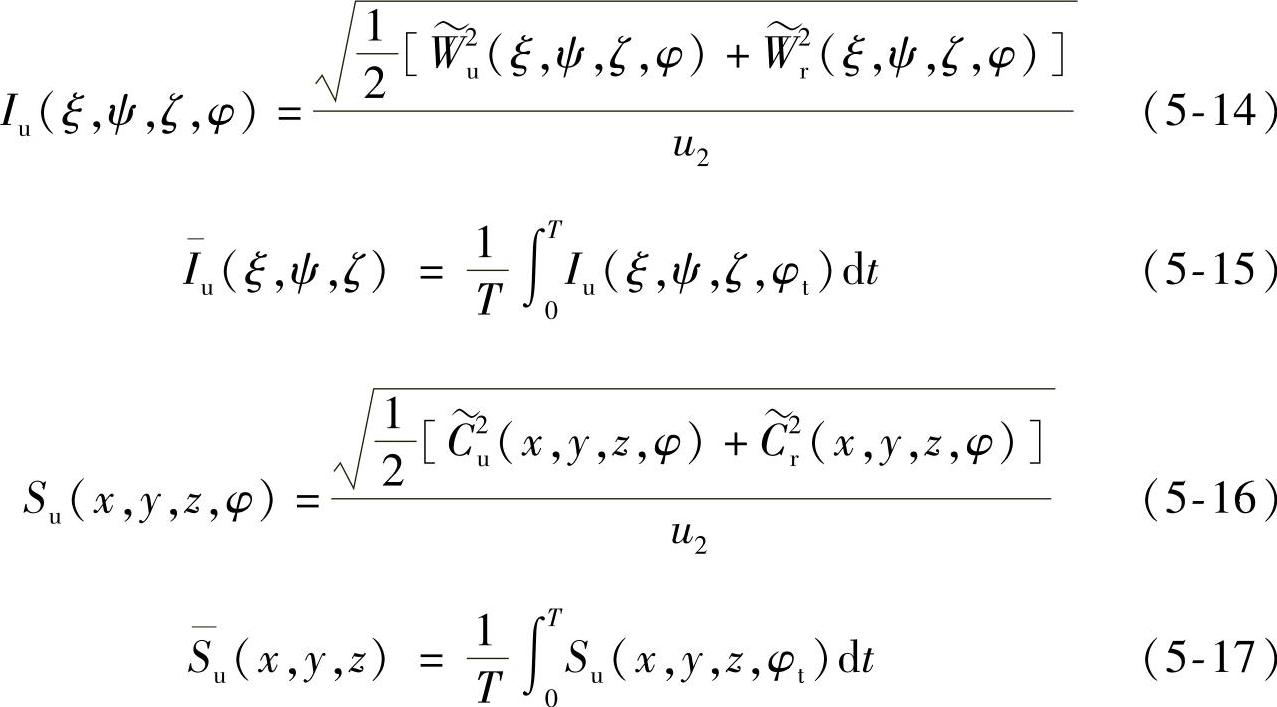
湍流强度T_u由式（5-18）和式（5-19）定义，式中k（x，y，z，φ）为湍动能。由于本章未考虑z轴方向上的非定常流动效应，即湍动能仅考虑2个方向的分量，因此根据各项同性假设，计算用的湍动能为原来的2/3。1个旋转周期的时均湍流强度系数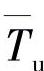可由式（5-20）计算。

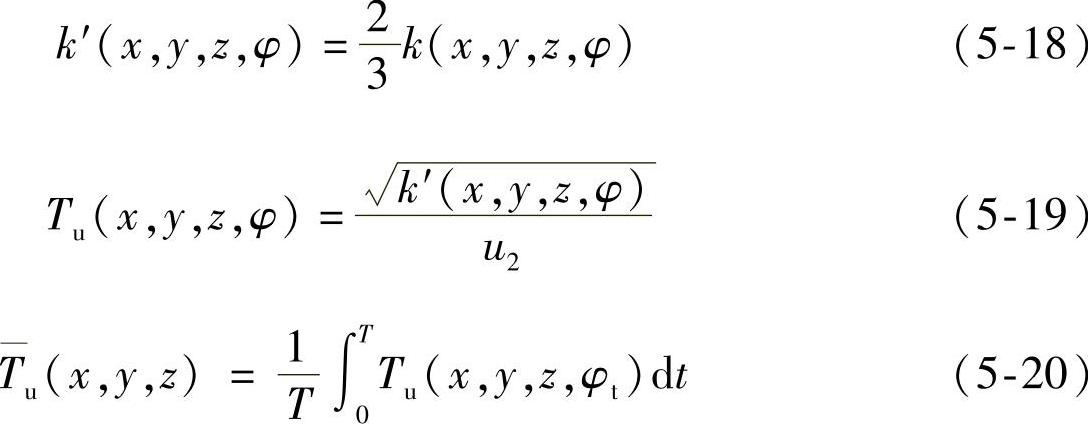
以上计算公式全部使用CFX CEL语言编程进行输入和定义。在CFX-Post中先定义表达式Expression，再定义变量Variable，通过读取1个旋转周期内所有时间步的计算结果来计算，这样就在每个网格节点上实现对自定义变量的计算，从而获得整个流道区域内的周期性非定常流动强度和湍流强度数据。

在非定常数值计算过程中研究CFX不同残差收敛曲线的差别，如图5-4和图5-5所示分别是CFX-Solver中的MAX残差收敛曲线和RMS残差收敛曲线。从对比结果可以看出，当MAX残差曲线达到10^-3收敛准则时，RMS残差曲线已基本达到10^-5目标。这是因为，MAX残差收敛标准意味着在所有网格节点中的最大残差要小于10^-3，而所有网格节点上残差值的均方根值一定更小；反之，如果均方根值小于10^-5，则不能保证所有网格节点上的残差MAX值一定都小于10^-3，有些网格节点残差值可能不达标，影响计算的准确性。因此，根据计算过程的经验可知，在非定常计算的每个时间步长中，只有当设定MAX残差收敛曲线

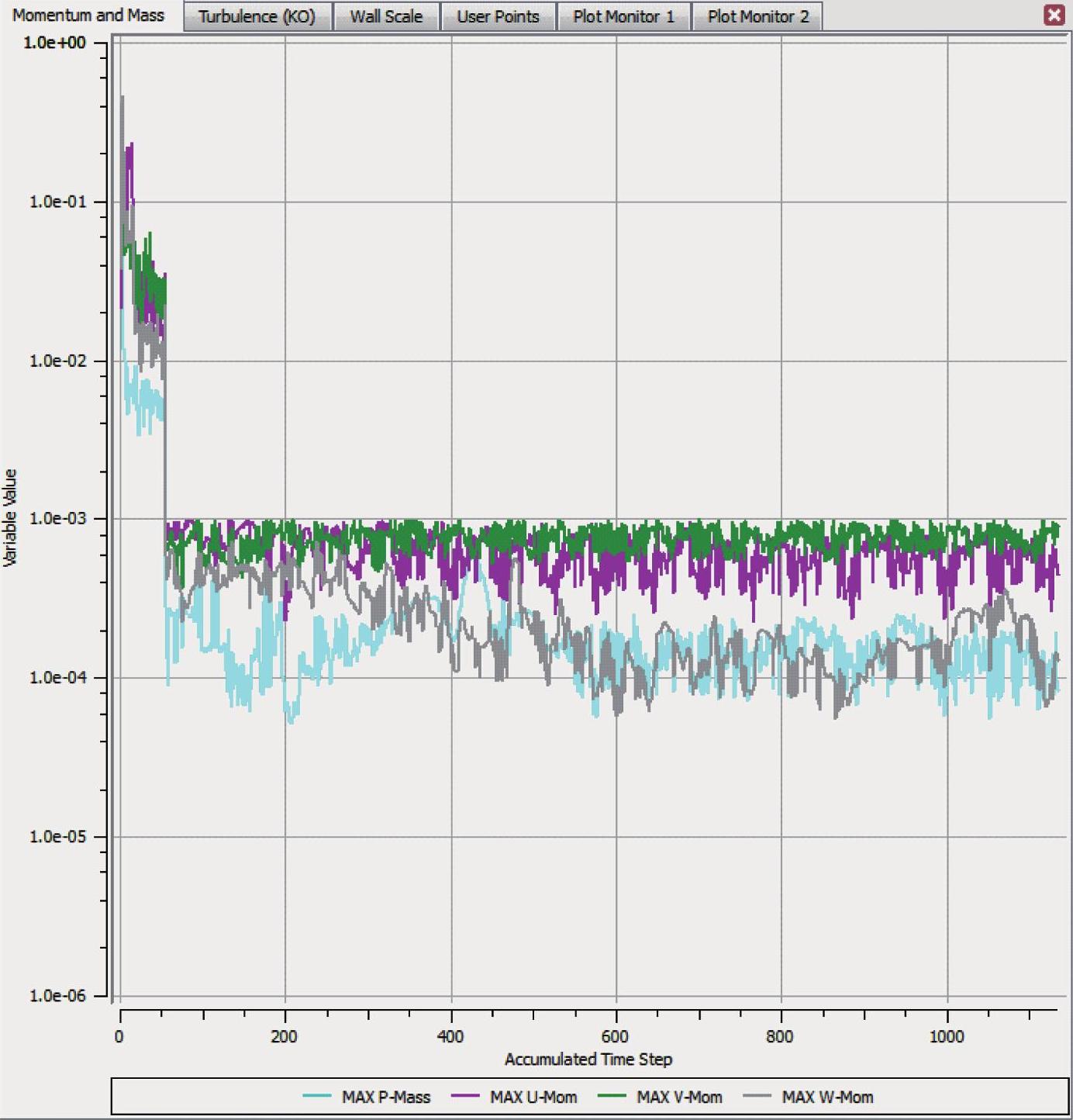
图5-4 CFX-Solver MAX残差收敛曲线

至少达到10^-3时，计算结果才更为精确。

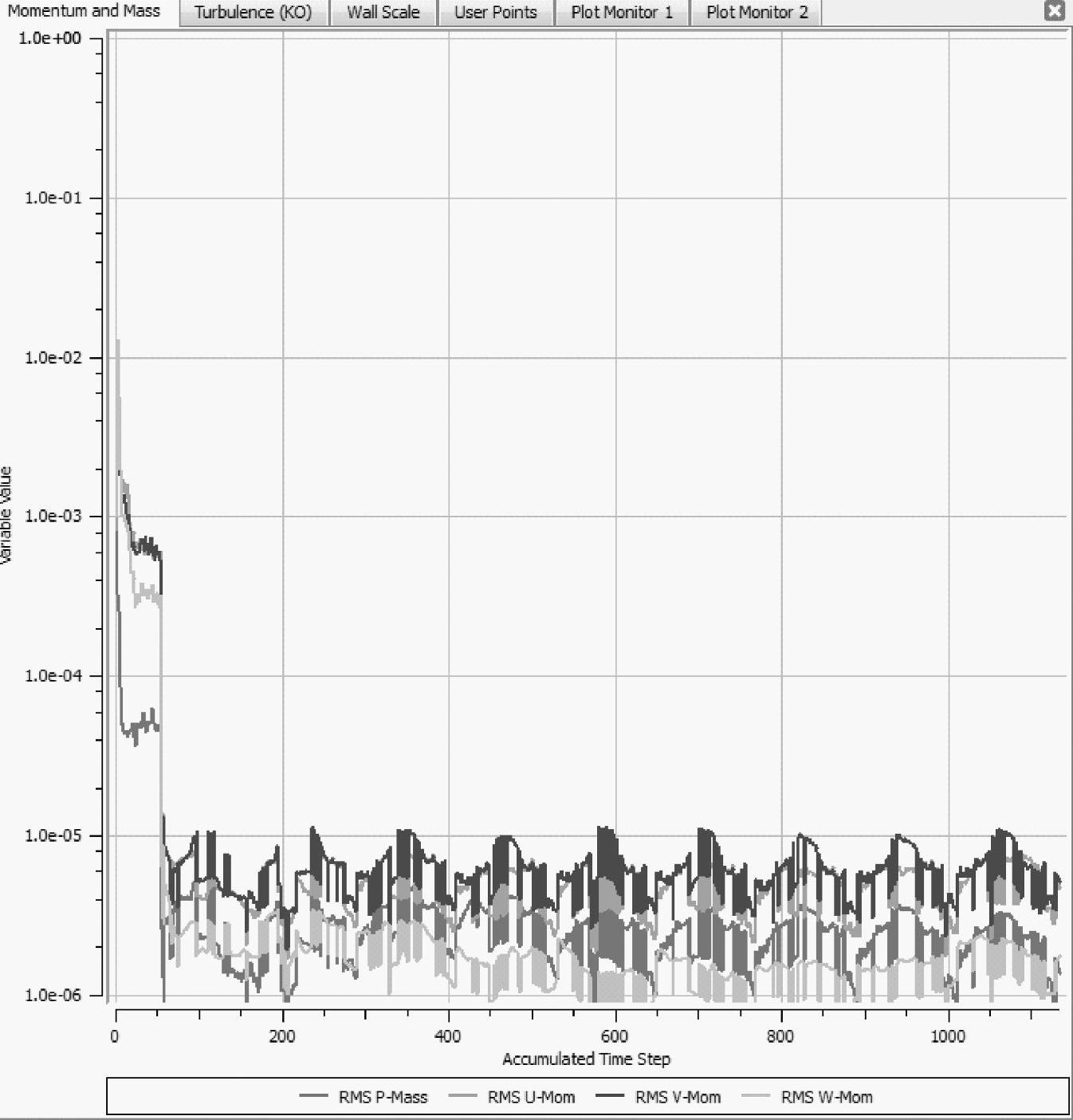
图5-5 CFX-Solver RMS残差收敛曲线