动应力是结构在动载荷作用下所产生的应力。在流固耦合计算过程中,离心泵叶轮结构受到复杂的非定常流动载荷作用,产生动应力分布。动应力分布会对结构的安全产生威胁,这是因为即使应力值没有达到结构的极限应力,但结构表面的动应力分布因长期存在引起结构疲劳破坏。因此,对水力机械进行基于流固耦合作用的动应力分析是十分必要的。
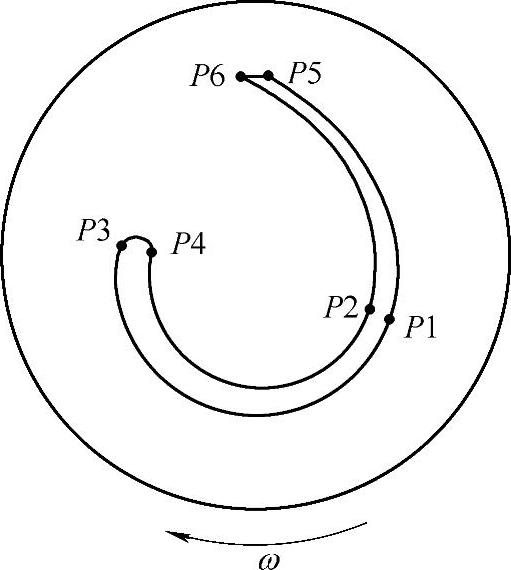
图4-49 叶片应力监测点位置示意图(Mid-span)
如图4-49所示是叶片应力监测点位置示意图(Mid-span)。本节分别取叶片中截面上6个典型位置(P1至P6)进行动应力结果的计算,分析不同工况下叶轮叶片前缘、后缘和叶片中部工作面和背面处的动应力分布特性。在分析动应力分布时引入等效应力的概念,即应用第四强度理论来定义等效应力σeq,也即Von Misesstress。
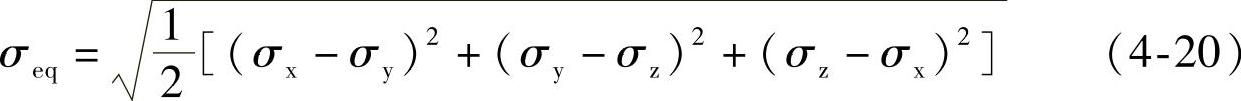
式中,σx、σy和σz分别为第一、第二和第三主应力。
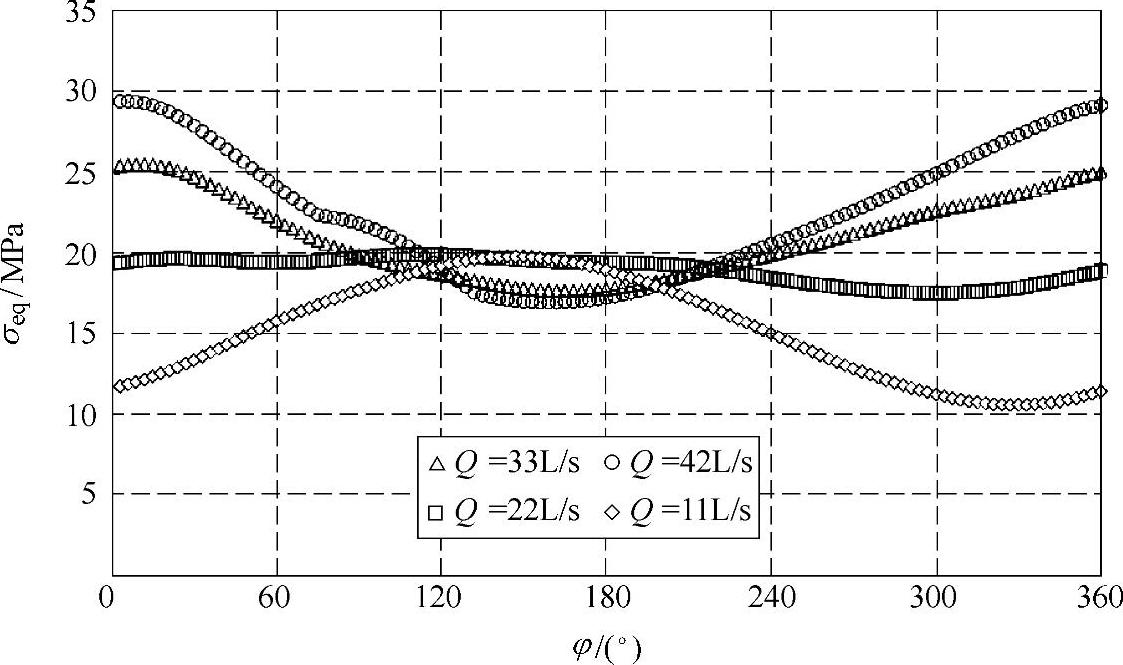
图4-50 n=1440r/min各工况下叶轮最大等效应力随时间变化的曲线
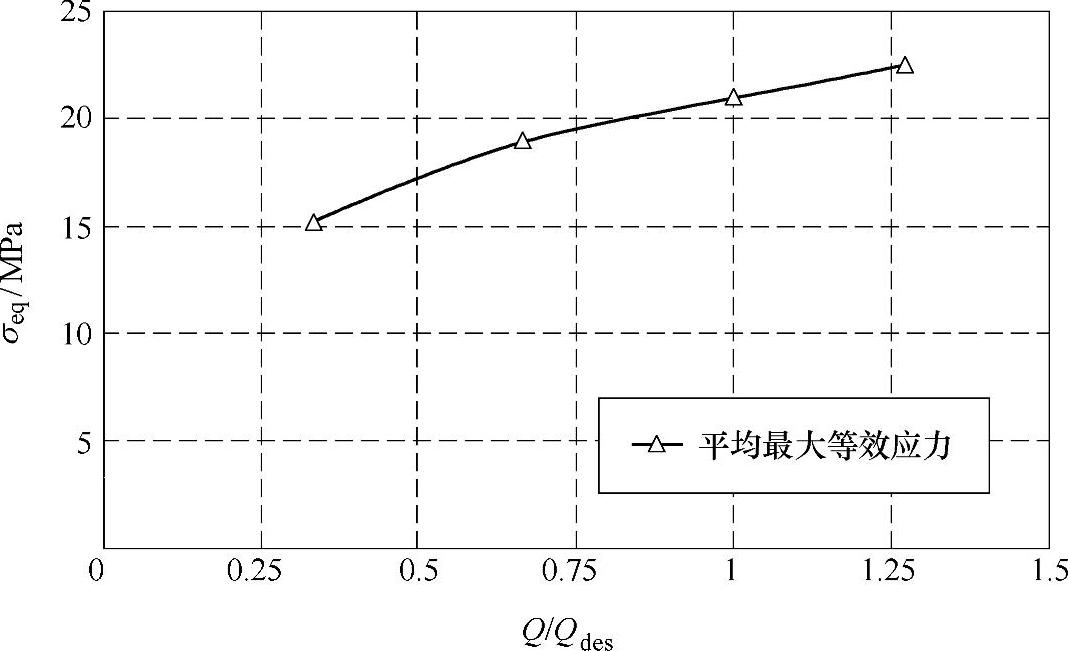
图4-51 n=1440r/min各工况下叶轮平均最大等效应力随流量的变化曲线
如图4-50和图4-51所示分别是额定转速下各工况叶轮最大等效应力随时间变化的曲线和平均最大等效应力随流量的变化曲线。图中的最大应力随时间变化曲线中最大值约为30MPa。从图中可以看出,在Q=33L/s、Q=42L/s和Q=11L/s的流量工况下,动应力曲线有明显波动,而对Q=22L/s流量工况,动应力曲线较平坦;小流量工况下动应力曲线相位明显不同于设计流量和大流量工况;最大应力的平均值随着流量的增加而增大。
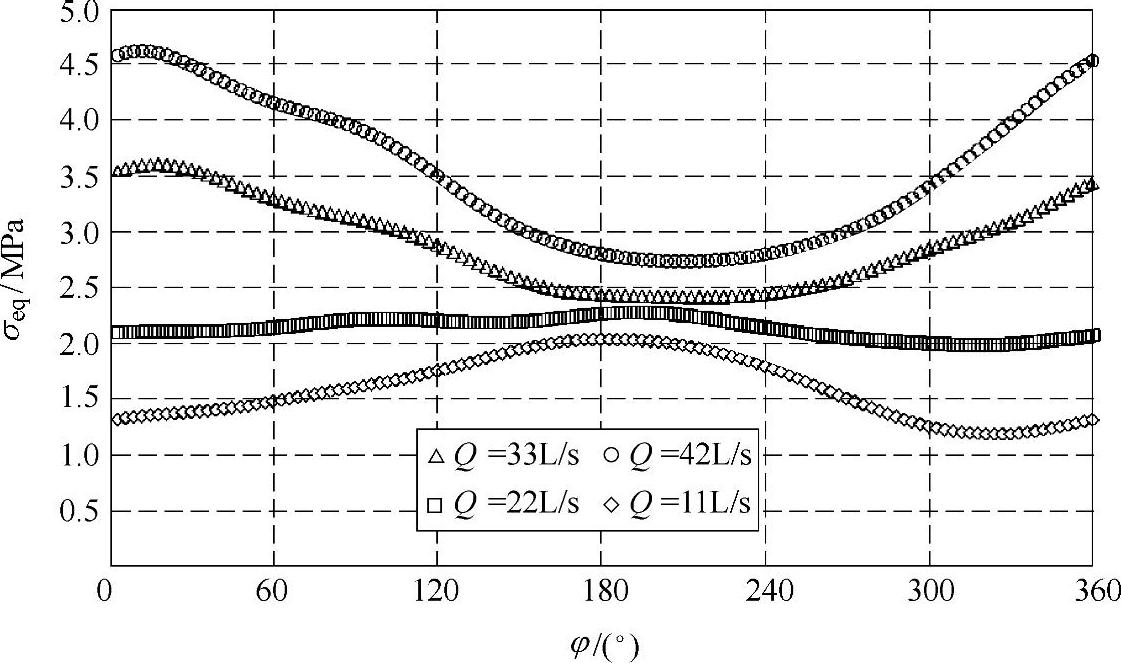
图4-52 n=1440r/min各工况下叶片动应力监测点P1的等效应力随时间变化的曲线
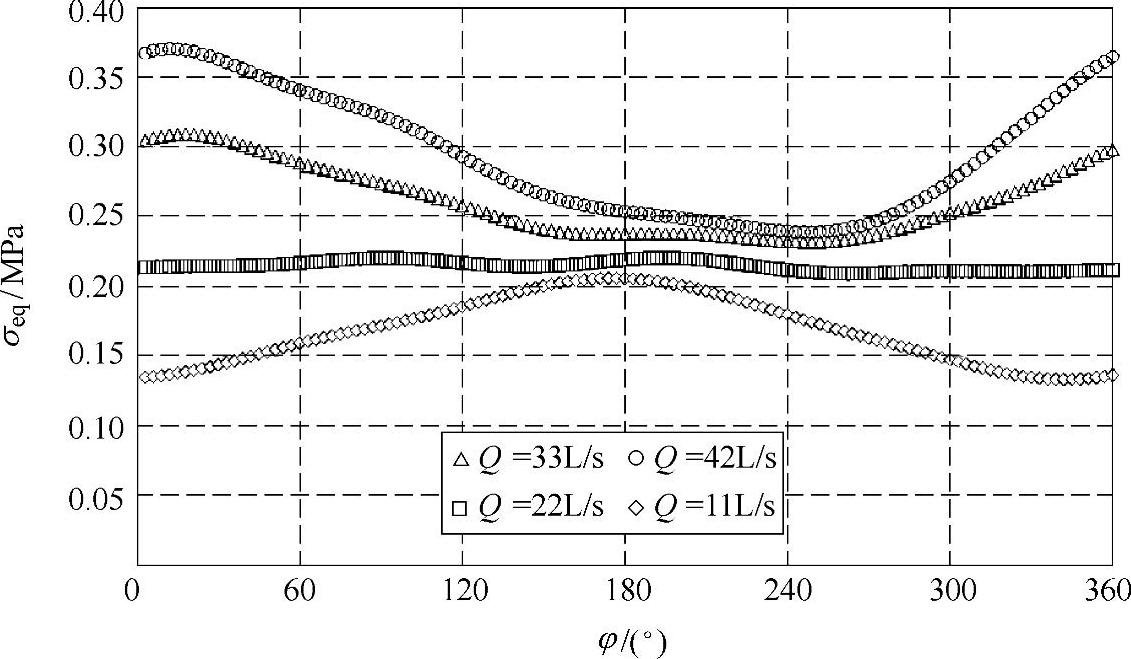
图4-53 n=1440r/min各工况下叶片动应力监测点P2等效应力随时间的变化
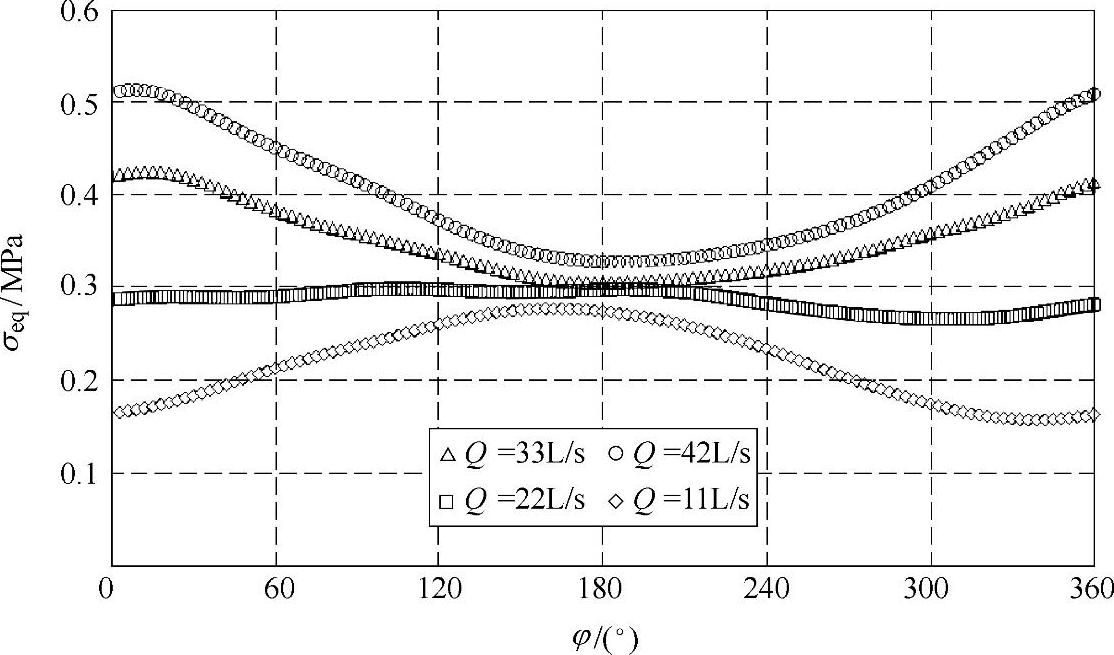
如图4-52~图4-57所示是各工况下叶片动应力监测点P1至P6的等效应力随时间变化的曲线。从这些图中可以发现,在叶片工作面上的
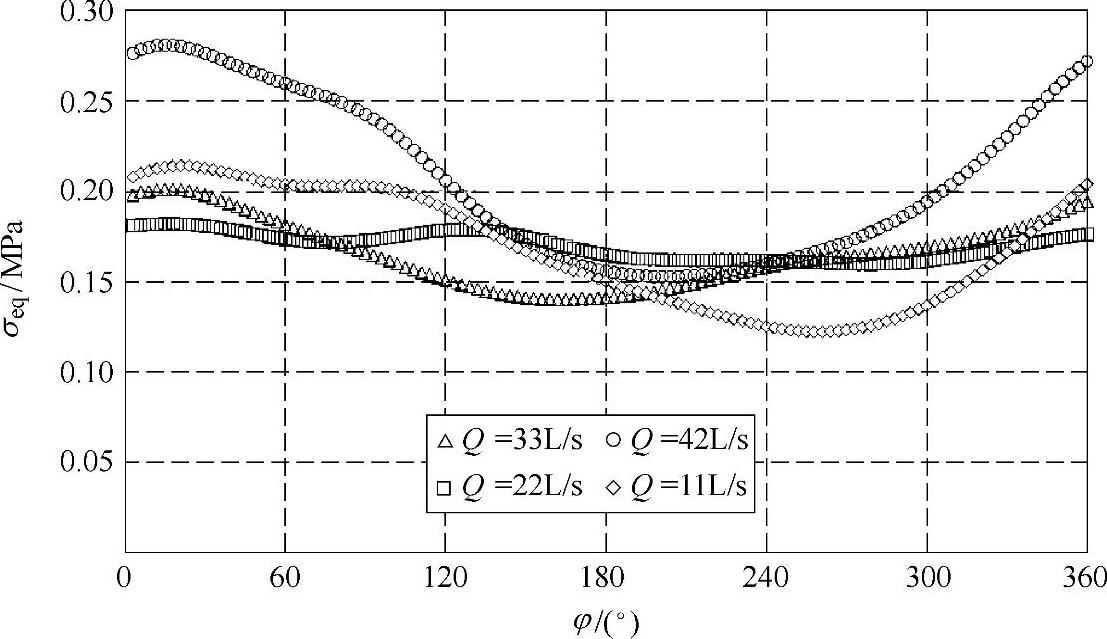
图4-54 n=1440r/min各工况下叶片动应力监测点P3等效应力随时间的变化
 (www.daowen.com)
(www.daowen.com)
图4-55 n=1440r/min各工况下叶片动应力监测点P4等效应力随时间的变化
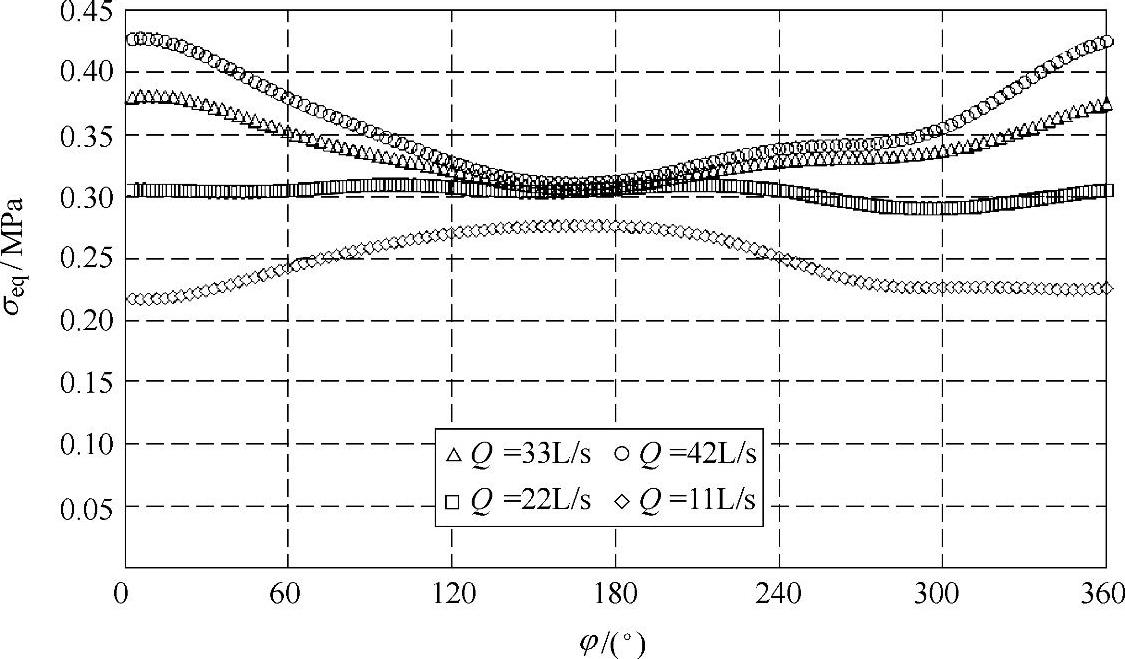
图4-56 n=1440r/min各工况下叶片动应力监测点P5等效应力随时间的变化
监测点P1,等效应力值的分布相对较大,在1~5MPa范围内,而其他各监测点处的等效应力值均小于1MPa;与上述最大应力值分布规律相似,对Q=33L/s、Q=42L/s和Q=11L/s流量工况,监测点P1、P2、P4、P5和P6上动应力曲线有明显波动,而对Q=22L/s流量工况,动应力曲线较平坦;小流量工况下动应力曲线相位明显区别于设计流量和大流量工况;当叶轮在φ=120°~240°范围内旋转时,流量对动应力的影响较小,而在φ=0°附近,流量对动应力大小影响最明显。在叶片前缘靠近工作面位置的监测点P3,各工况下动应力分布比较复杂,与其他监测点不同,这可能是因为在叶片前缘靠近工作面的位置流动不稳定,流体对结构的作用随流量的变化比较复杂。
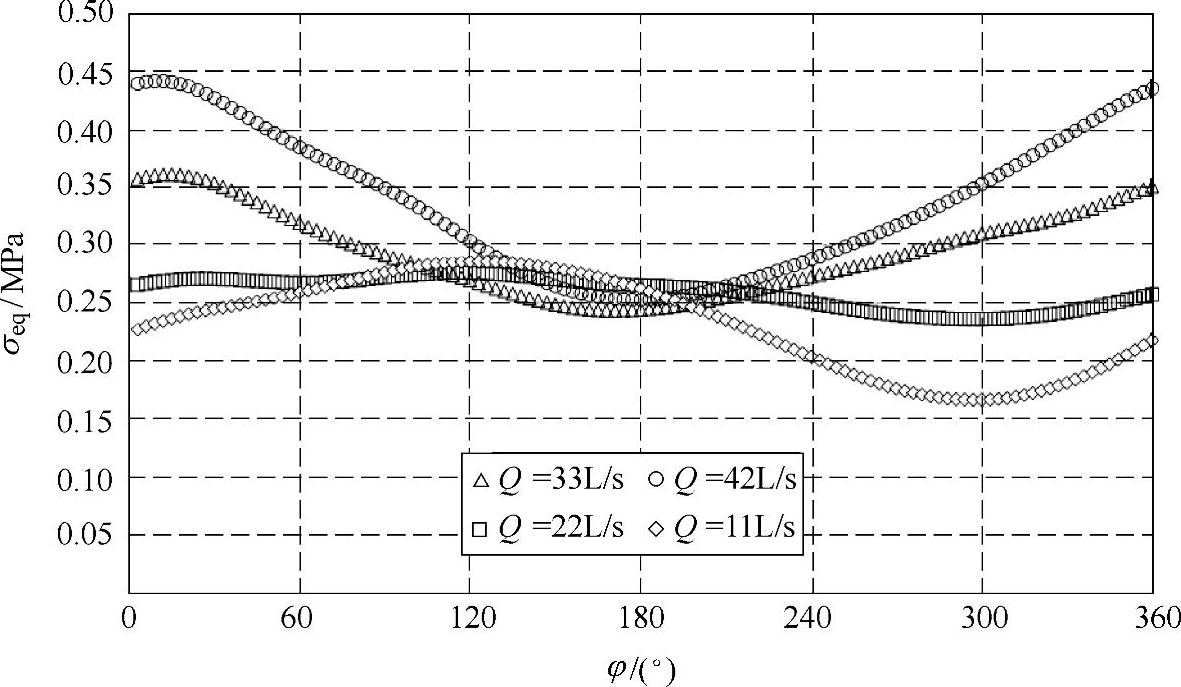
图4-57 n=1440r/min各工况下叶片动应力监测点P6等效应力随时间的变化
如图4-58所示是φ=0°时各工况下中截面上叶片1周的等效应力分布。图中N表示沿着叶片某一方向连续选取的采样点编号,叶片的前缘、后缘、工作面和背面位置在图中分别用LE、TE、PS和SS标示。在叶片后缘附近,各流量下等效应力值出现峰值,同时出现明显的跳跃;在叶片前缘位置附近,各流量下等效应力值出现两个峰值;在叶片背面中部,等效应力从后缘向前缘逐渐减小,在后缘附近,出现了1个波谷;在叶片工作面中部,应力值从叶片前缘向后缘增加。总体上,等效应力值随着流量的增加而增加。
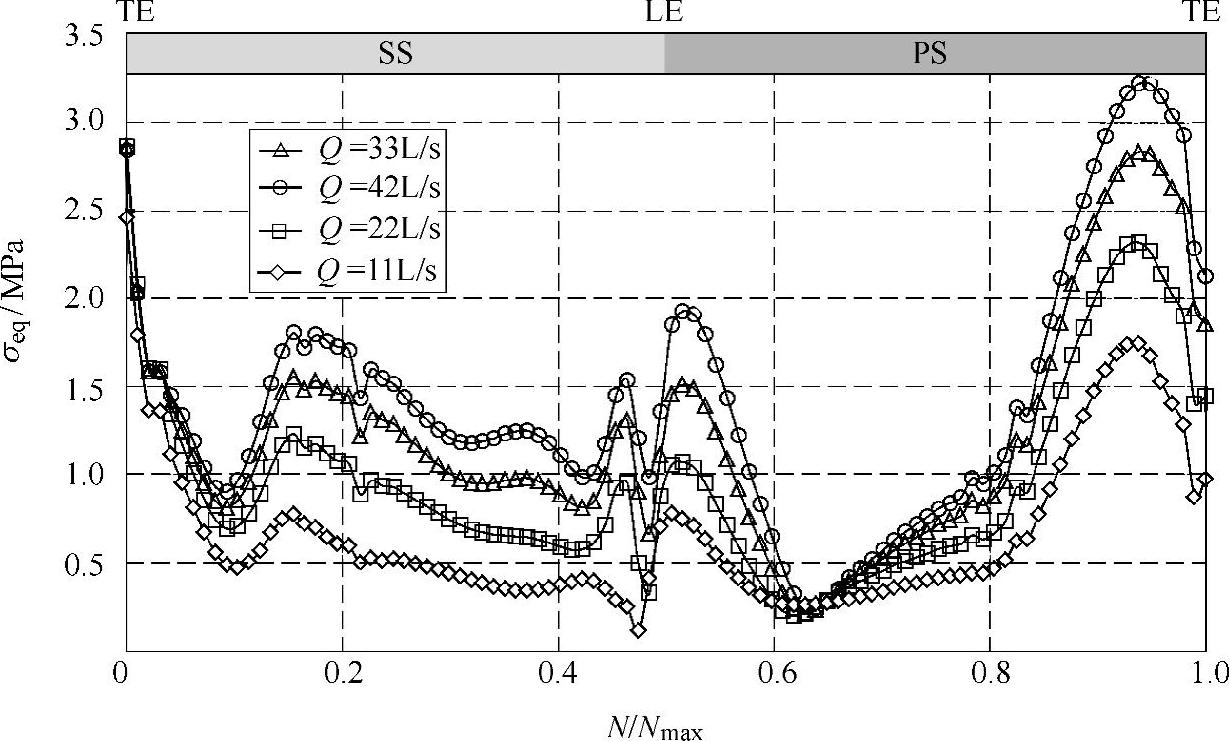
图4-58 n=1440r/min,φ=0°时各工况下中截面上叶片1周等效应力分布
如图4-59所示是φ=0°时各流量工况下叶片等效应力分布情况。从图中可看出,相对较大的等效应力值出现在靠近后缘处;而叶片前缘附近应力值分布相对较小。此外,流量的变化对等效应力的影响十分明显,应力值随着流量的增加而增大。
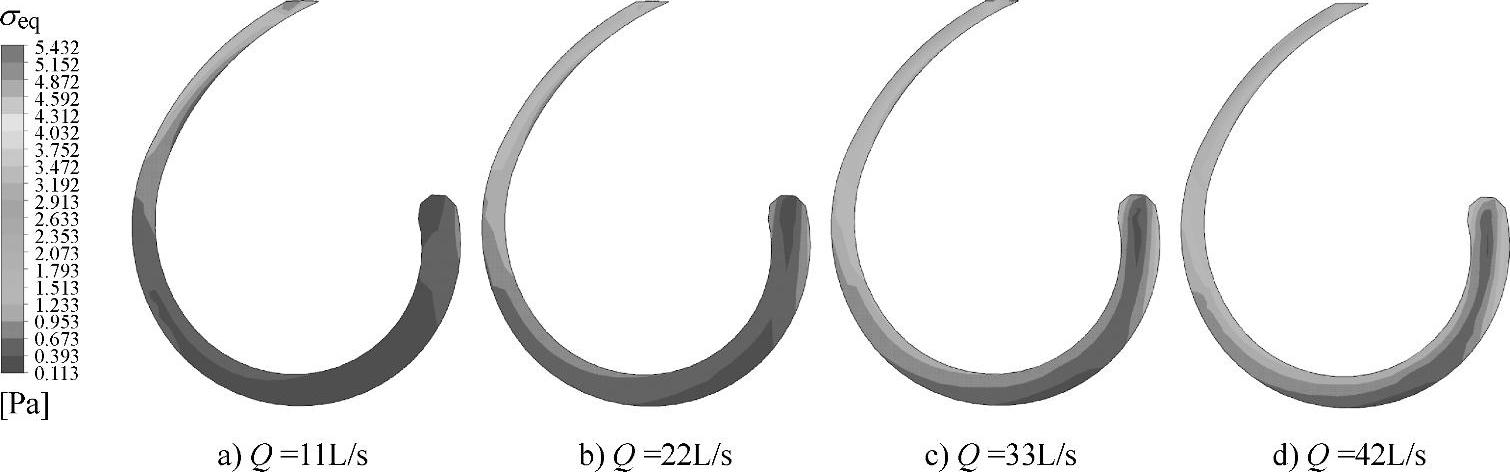
图4-59 n=1440r/min,φ=0°时各工况下叶片等效应力分布
如图4-60所示是φ=0°时不同流量工况下叶轮等效应力的分布情况示意图。从图中可以清楚地看到,随着流量的增大,等效应力相对较大的区域逐渐变大。在流量Q=11L/s工况下,等效应力较大的区域面积很小;在流量Q=22L/s工况下,在叶片后缘和工作面靠近后盖板的位置开始可以看到应力相对较大的区域;对于流量Q=33L/s工况下,该区域继续变大,还出现在叶片后缘靠近前盖板的位置;对于大流量工况,等效应力相对较大区域达到最大,并且可以在叶片工作面明显地看到。
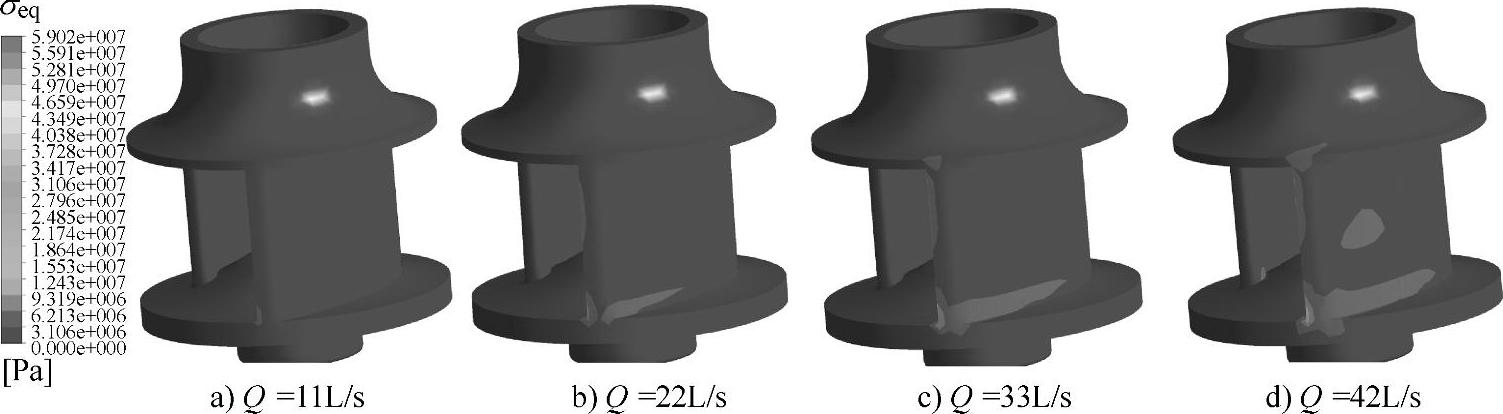
图4-60 n=1440r/min,φ=0°时各工况下叶轮等效应力分布示意图
如图4-61所示是设计流量下φ=0°时叶轮轴上等效应力的分布情况。从图中可以看出,整个转子系统的最大应力值出现在松轴承安装位置附近,双向流固耦合求解得的最大等效应力值大于40MPa。

图4-61 n=1440r/min,设计流量Q=33L/s且φ=0°时叶轮轴等效应力分布
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







