本节对细网格双向流固耦合求解的叶轮振动位移结果进行分析，并与试验测量的振动结果进行对比。在双向流固耦合计算过程中，旋转坐标系下的叶轮振动取值位置为叶轮进口外圆处，见图4-6。由前述可知，该点的取值结果为旋转坐标系下的位移结果，需要转换为静止坐标系下的结果与试验测量结果再进行对比。

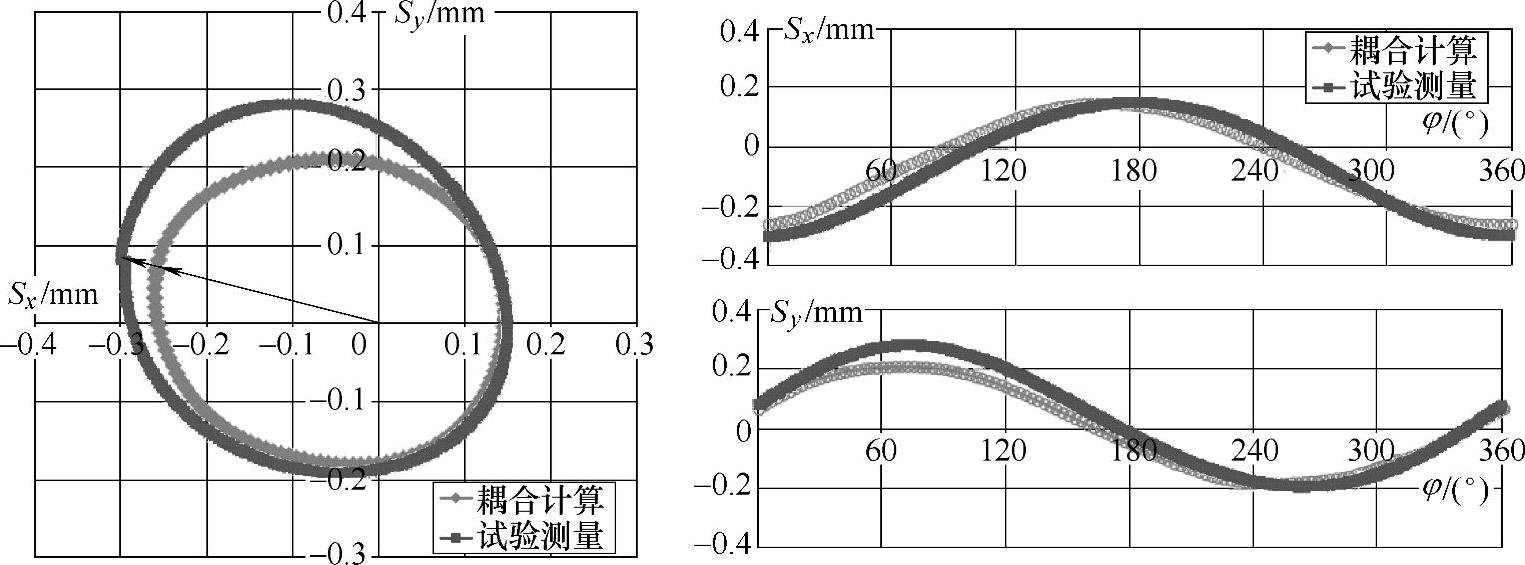
图4-34 n=1440r/min，Q=42L/s工况下流固耦合计算与试验测量的振动位移结果对比

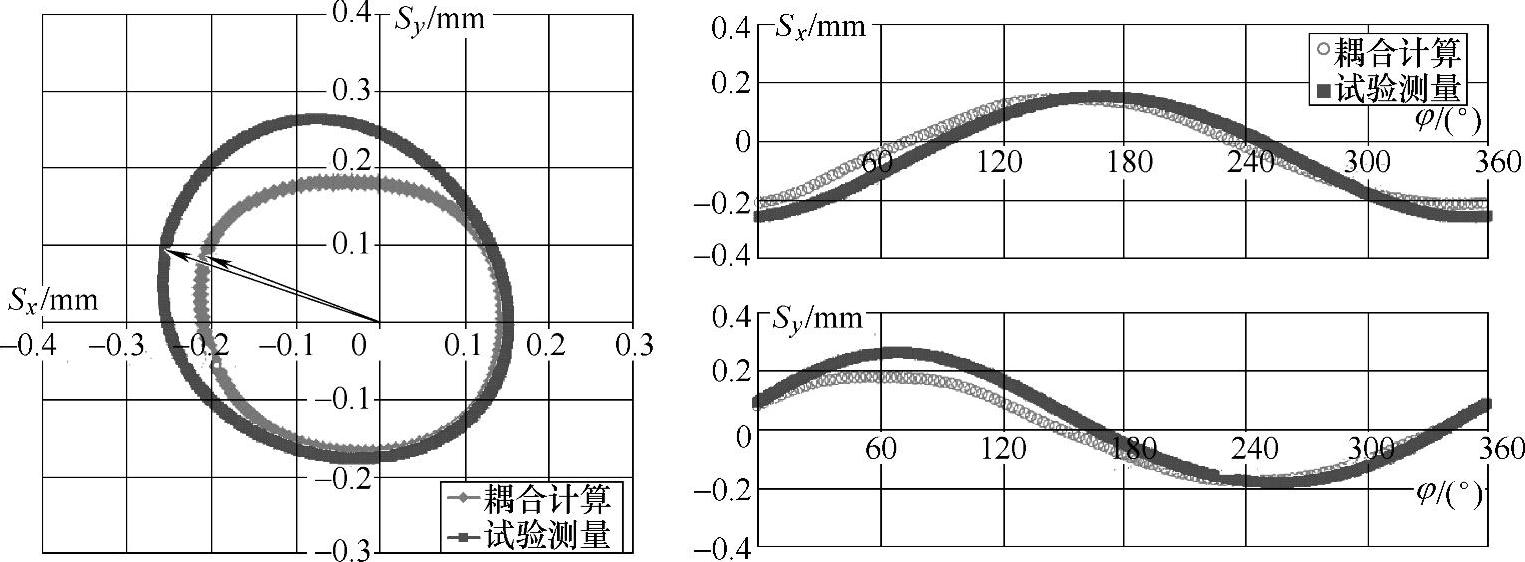
图4-35 n=1440r/min，Q=33L/s工况下流固耦合计算与试验测量的振动位移结果对比

如图4-34～图4-37所示为额定转速下各工况流固耦合计算与试验测量的振动位移结果对比，各图中左侧图为平面振动轨迹曲线结果，右侧图为x和y方向分量上的结果。从这些图中可以看出，振动位移随着流量的增大而增大。总体上，计算结果与试验测量结果吻合较好，特别是大流量和设计流量工况下，在静止坐标系下的第一、三和四象限内振动位移大小基本一致，在第二象限内振动位移大小有一定差别，且振动测量幅值略大于流固耦合计算的值。大流量工况下计算和测量的相位结果吻合很好，准确捕捉了振动相位信息。对小流量工况，位移大小的计算和测量结果差别相对较明显，且随着流量的减小，差别变得明显。位移曲线相位的流固耦合数值预测也产生了一定偏差，试验测量得到的振动

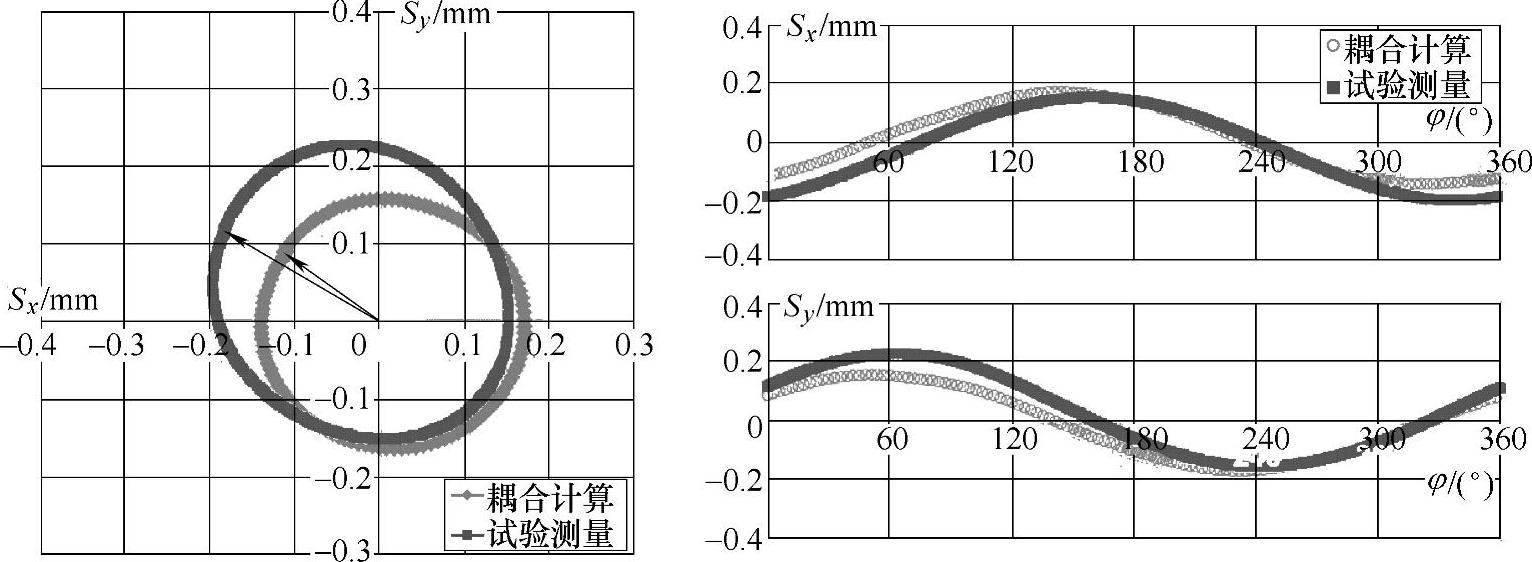
图4-36 n=1440r/min，Q=22L/s工况下流固耦合计算与试验测量的振动位移结果对比

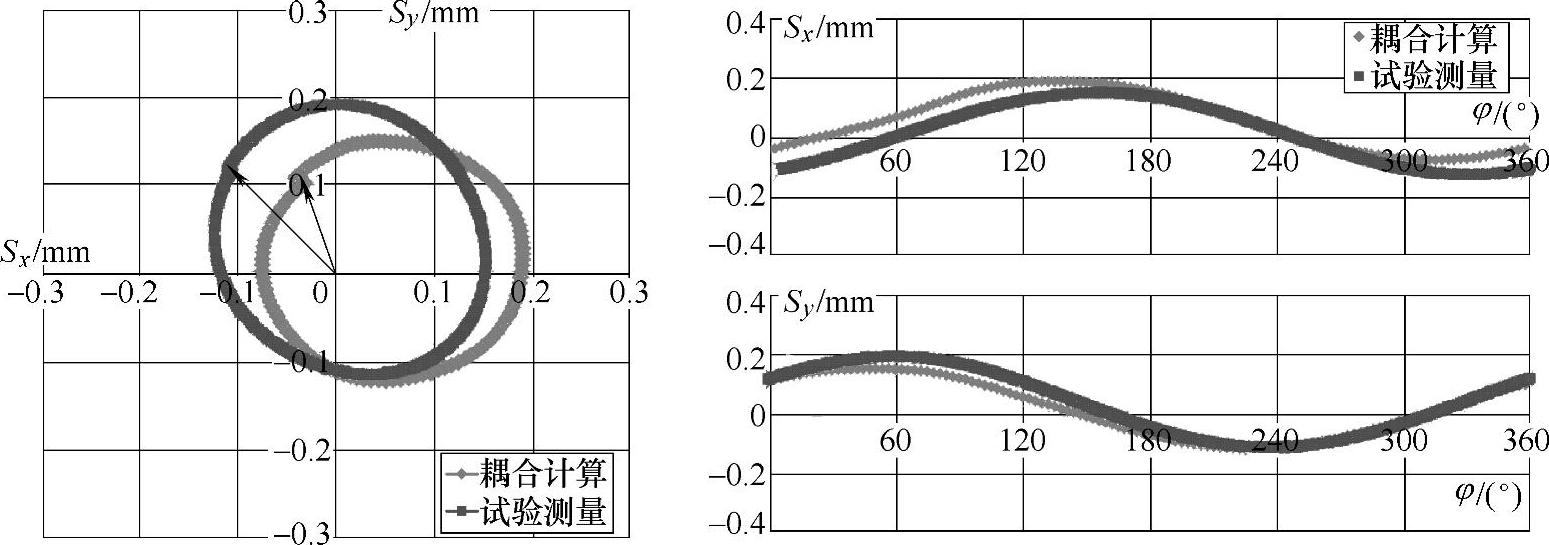
图4-37 n=1440r/min，Q=11L/s工况下流固耦合计算与试验测量的振动位移结果对比

曲线相位要滞后于计算所得的结果，且随着流量的减小，相位差别越明显。由以上分析可知，对于本书所建立的流固耦合计算，随着流量的增加，预测结果越准确。在小流量工况下，预测结果在振动位移的幅值和相位两方面都产生了一定的偏差，这应该与URANS方程在预测小流量工况下离心泵内部流动现象时存在一定偏差有关。此外，从对x和y方向分量上的振动位移进行对比的结果中可知，在x方向上，试验和计算结果的偏差主要在φ=0°～120°和φ=300°～360°范围内，且随着流量的增大而增大。对y方向上的分量，计算和试验的差别主要出现在φ=0°～180°的范围内。

如图4-38～图4-43所示分别是模型离心泵在低速运行工况（n=1250r/min和n=1000r/min）下的流固耦合和试验测量振动位移结果对比。从中可以看出，计算和测量结果的关系与额定转速下的基本一致。在阀门全开的大流量工况下，预测和试验的振动幅值吻合相对最好，但在第二象限内存在一定的偏差；预测和测量的振动相位值完全吻合。在其他流量下，振动幅值的预测偏差随着流量的减小而增大，相位的预测在小流量下可以看到明显的差异，测量的相位要滞后于耦合计算所得的值。

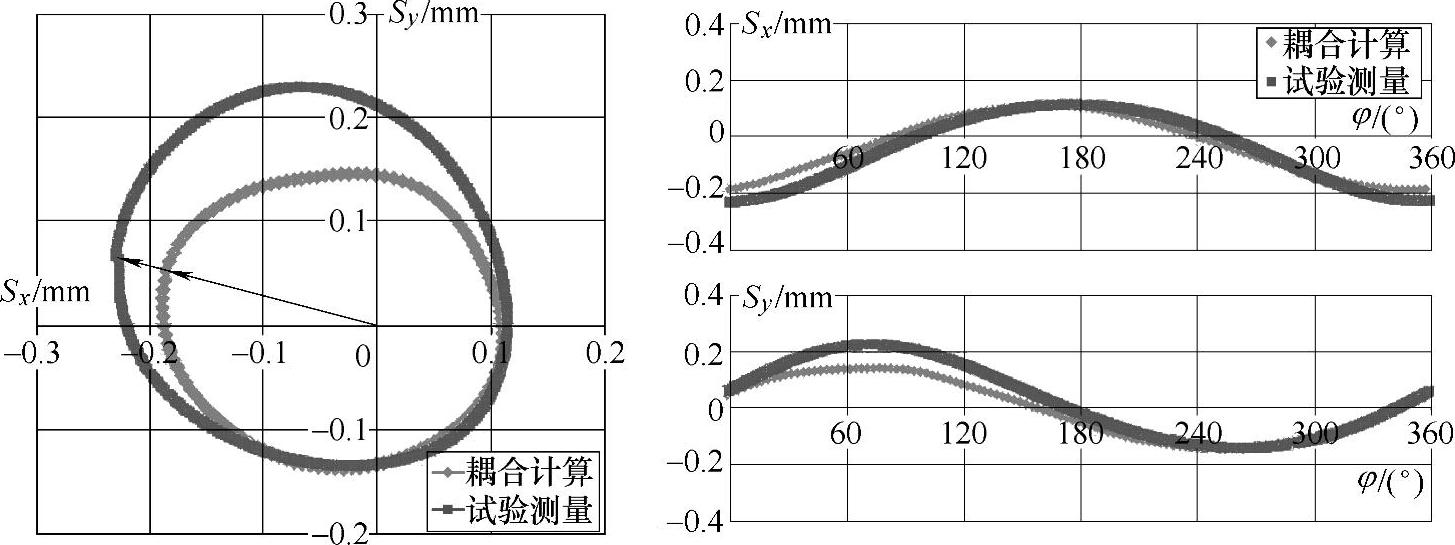
图4-38 n=1250r/min，Q=35L/s工况下流固耦合计算与试验测量的振动位移结果对比

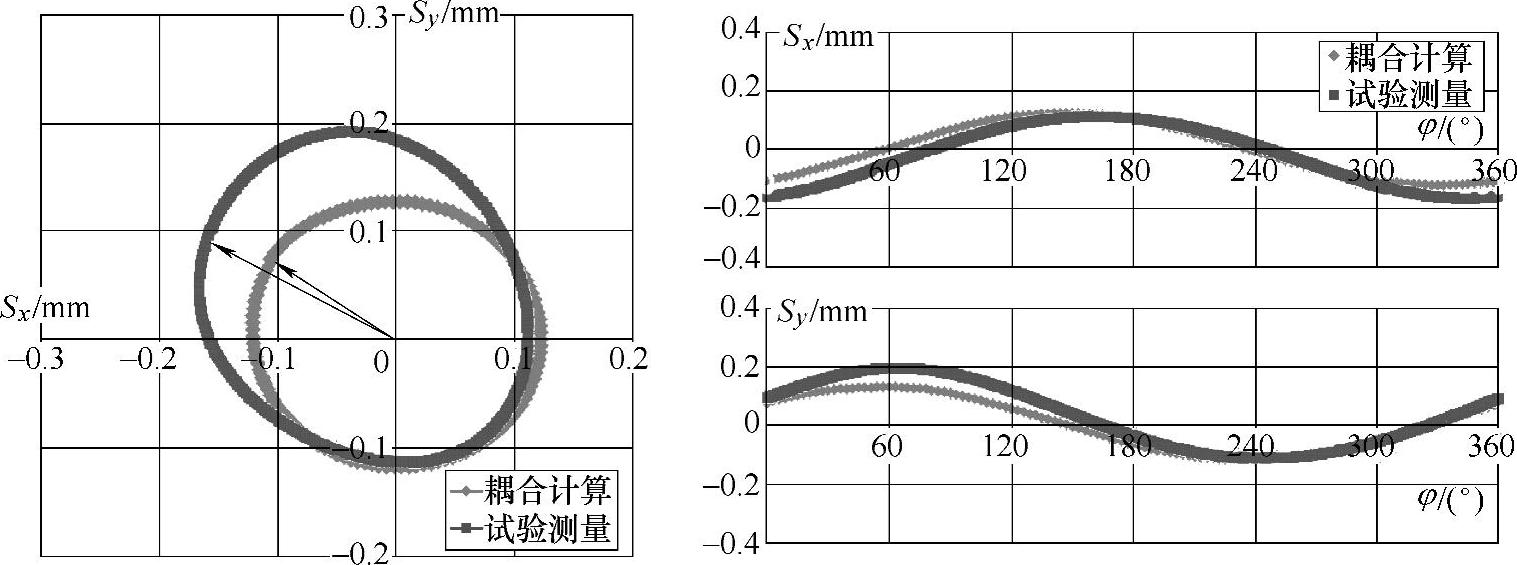
图4-39 n=1250r/min，Q=22L/s工况下流固耦合计算与试验测量的振动位移结果对比

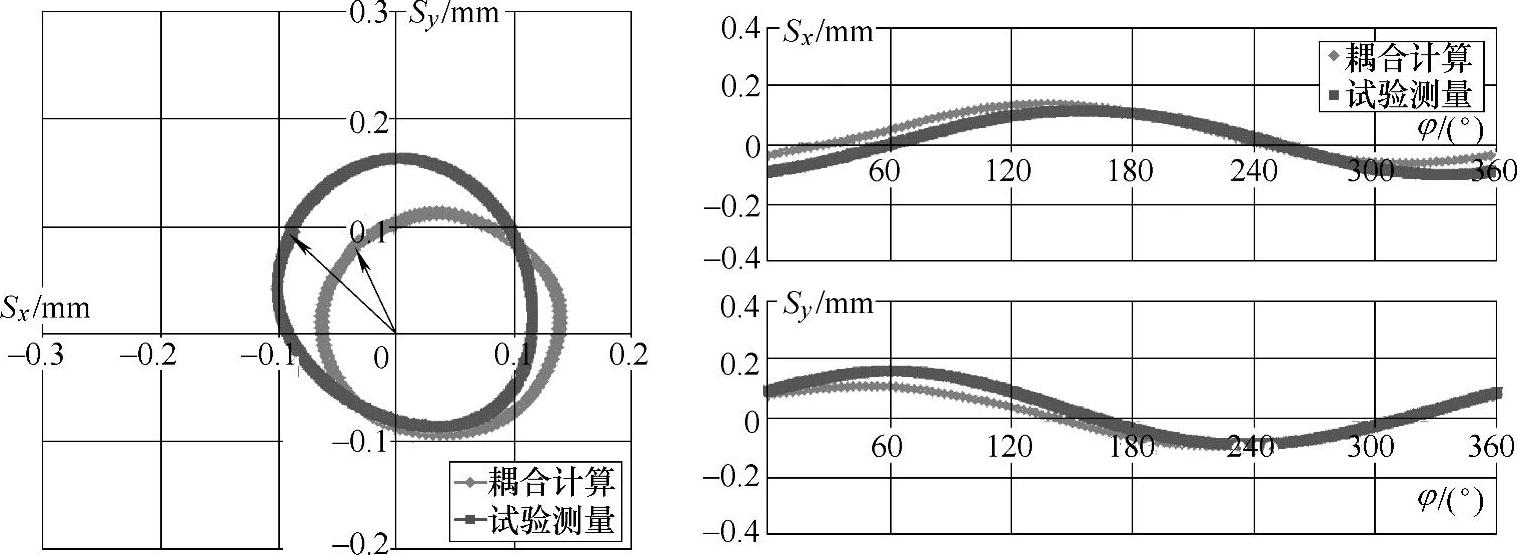
图4-40 n=1250r/min，Q=11L/s工况下流固耦合计算与试验测量的振动位移结果对比

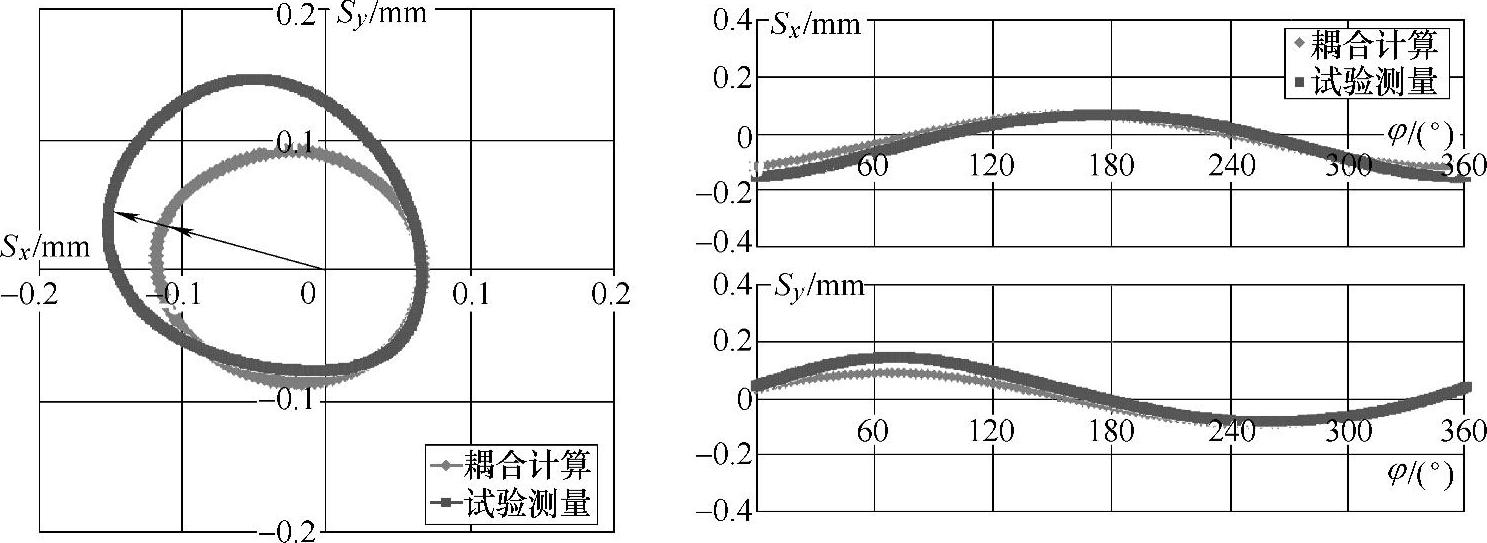
图4-41 n=1000r/min，Q=27L/s工况下流固耦合计算与试验测量的振动位移结果对比(www.daowen.com)

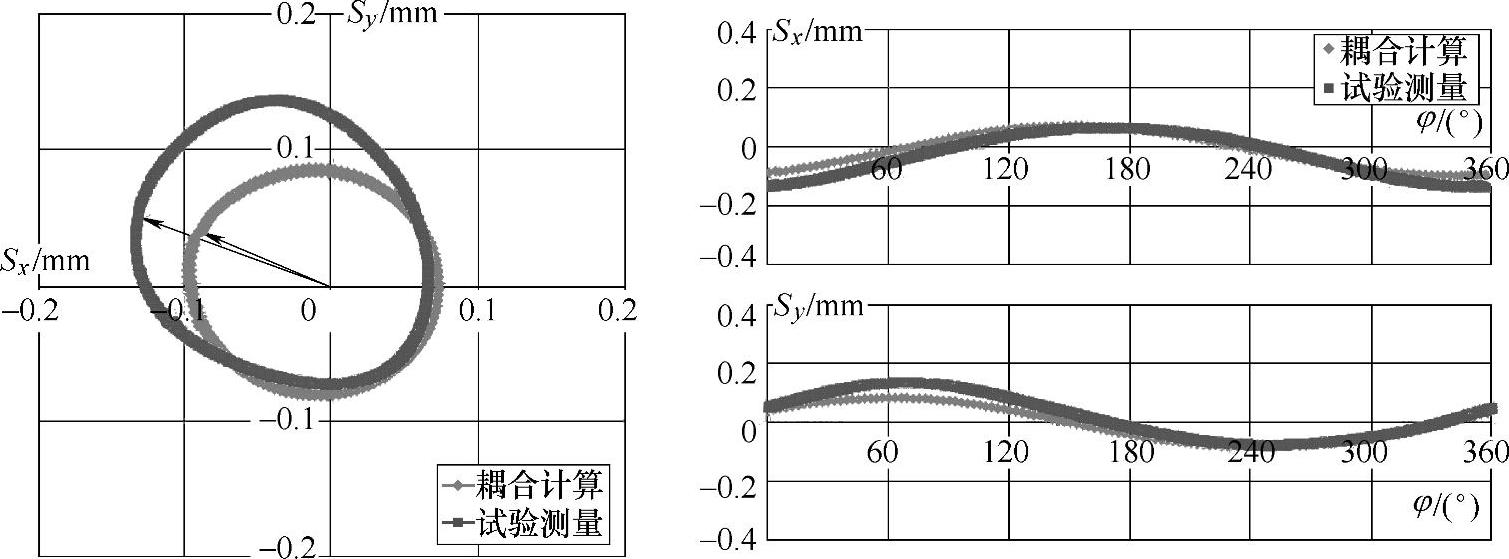
图4-42 n=1000r/min，Q=22L/s工况下流固耦合计算与试验测量的振动位移结果对比

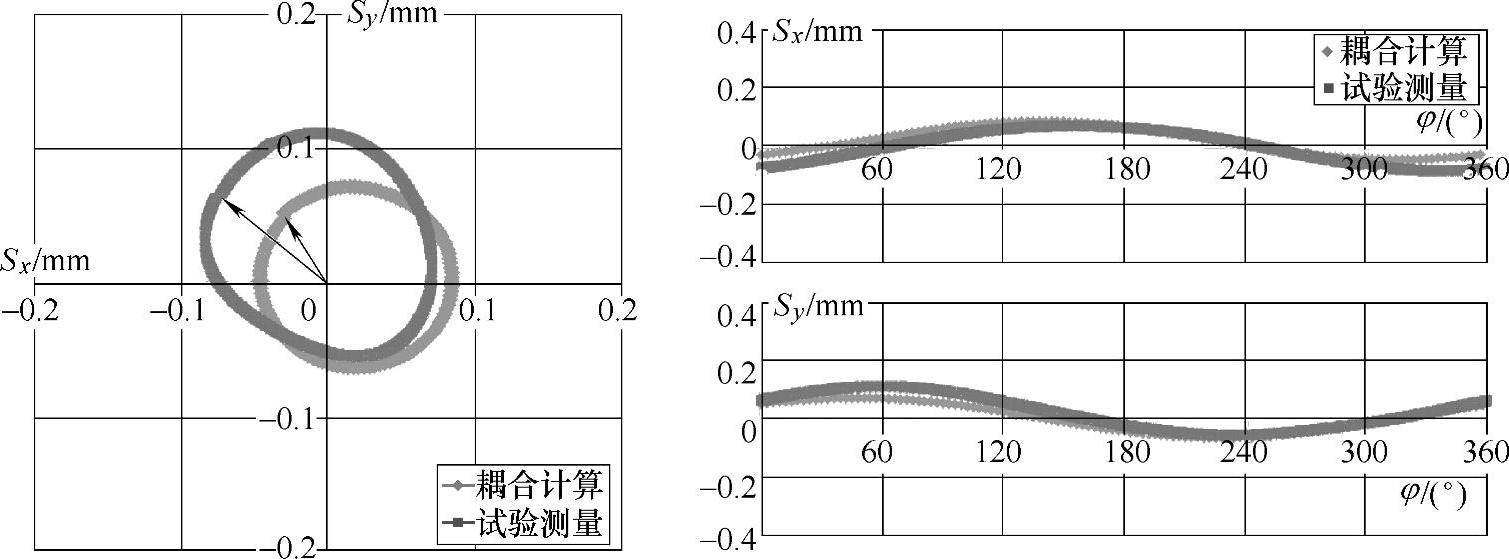
图4-43 n=1000r/min，Q=11L/s工况下流固耦合计算与试验测量的振动位移结果对比

如图4-44所示是额定转速下，不同耦合策略计算与试验测量的振动位移结果对比。在大流量和设计流量工况下，在第三、四象限以及第二象限部分区域内双向耦合结果略大于单向耦合结果，而在第一象限以及第二象限一部分区域内，两者结果差别不大，且两种耦合策略求解的相位差别不大。小流量工况下，在第一、二象限内双向流固耦合结果略大于单向耦合结果，在其他象限内两种耦合结果差别不大；两种耦合方式下的相位结果差别不大。

如图4-45所示是额定转速各工况下不同流体网格耦合计算与试验测量的振动位移结果对比分析。从图中可以看出，在大流量和设计流量工况下，细网格耦合计算的结果要明显大于粗网格计算的值，但相位基本一致。在Q=22L/s工况下，细网格耦合计算结果要大于粗网格结果，在第二象限差别较大。Q=11L/s工况下，在第一象限内，两种网格计算结果差别不大，在其他象限内，细网格结果大于粗网格计算结果。

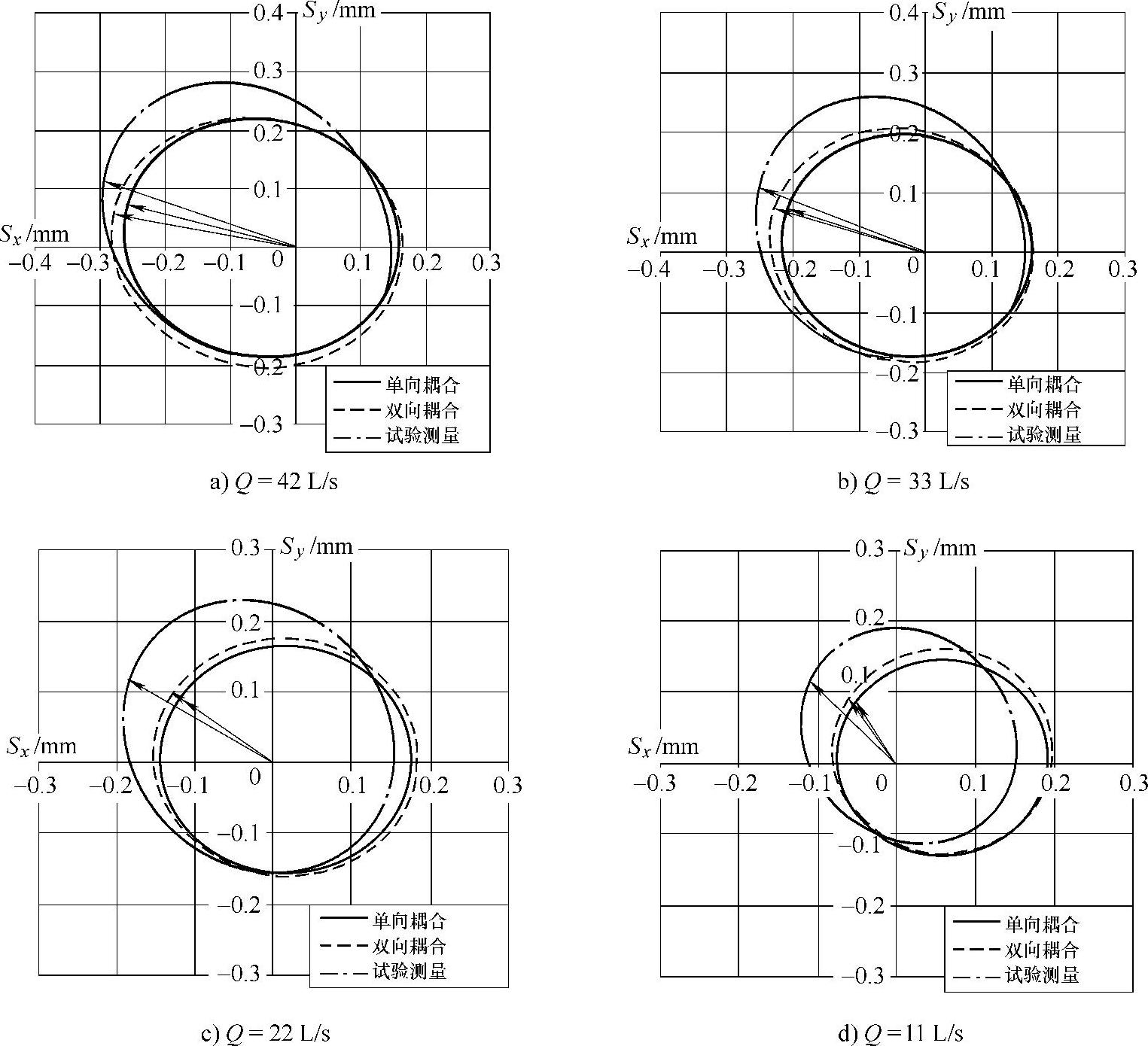
图4-44 n=1440r/min各工况下不同耦合策略计算与试验测量的振动位移结果对比

通过以上流固耦合叶轮水力激振位移结果与试验测量结果的对比可以发现，尽管流固耦合计算结果与试验值已经得到很好的吻合，但仍然存在一定的差别，偏差主要存在于第二象限。本书对试验和流固耦合计算过程中可能产生的误差进行了分析，总结出了可能造成该结果偏差的原因如下。

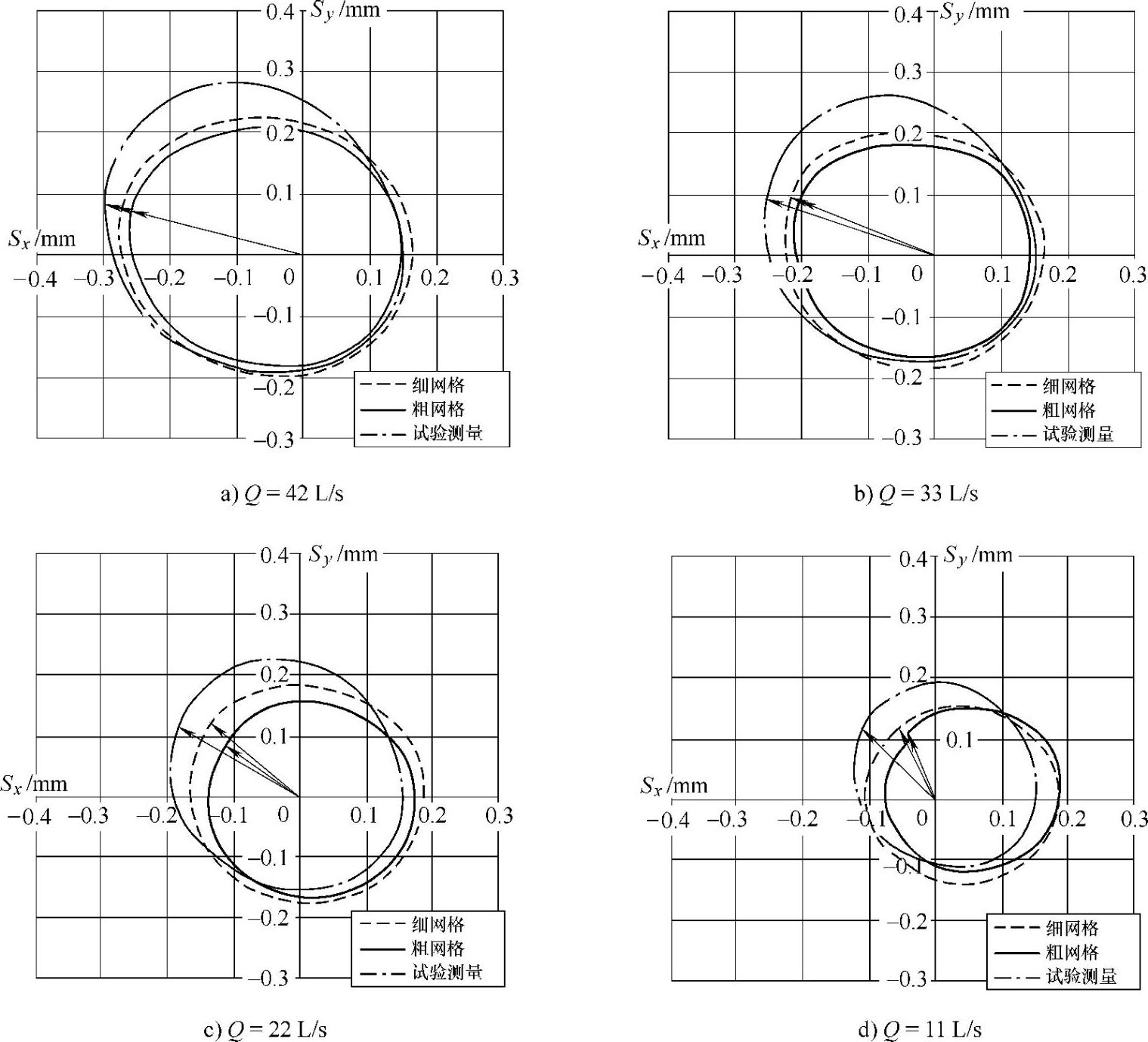
图4-45 n=1440 r/min各工况下不同流体网格耦合计算与试验测量的振动位移结果对比

1）在水力激振测量过程中，叶轮的动平衡不可能完全达到绝对的质量平衡，而流固耦合计算过程中，叶轮振动的仿真只考虑了水力激励的影响，没有考虑叶轮质量不平衡离心力的影响。

2）流固耦合计算过程中，没有考虑非对称的轴向力对转子产生的弯矩作用，该作用会影响径向振动结果的分析。

3）转子使用的滚柱轴承存在一定的间隙，流固耦合计算过程中没有进行考虑。

4）离心泵运行过程中轴承的动力学特性没有进行考虑，耦合计算过程中认为轴承是一个刚体，而实际工作中轴承会发生一定程度的变形。

5）振动测量过程中主要考虑的是叶轮在流体动静干涉作用下的位移，尽管本章耦合求解中的流场CFD结果也是以动静干涉作用为主，但会在一定程度上包含其他流动现象，特别是在小流量工况下。

6）本书流固耦合求解的是叶轮的振动，而实际测量过程中，离心泵的壳体也会受流动以及其他机械的影响而发生振动，测量转子振动的电涡量振动位移传感器安装在泵壳体上，因而，这种振动会在一定程度上影响传感器对转子位移测量的准确性。

7）转子对中性的误差会影响测量结果和流固耦合计算结果的吻合程度。

8）外部载荷传递式流固耦合求解过程中，数据载荷传递的收敛标准为默认值0.01，可使用更加苛刻的收敛标准，以便获得更精确的流固耦合求解结果。